人教A版高中数学必修二3.3.3 点到直线的距离(一)课件(共17张PPT)
文档属性
| 名称 | 人教A版高中数学必修二3.3.3 点到直线的距离(一)课件(共17张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 905.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-09 18:01:46 | ||
图片预览






文档简介
3.3 距离(1)
高中数学人教A版必修2
复习回顾:
平面几何中研究了几种距离,该怎样计算
点到点的距离
点到线的距离
两平行线间的距离
问题1:如何求点P (– 1 , 2) 到直线l:3x = 2的距离?
问题2:如何求原点O到直线l:3x + 2y – 26 = 0的离?
问题探究3:如何求点到直线的距离?
直线 的距离.
( 不在直线 上,且 , ),试求 点到
已知: 和直线 :
分析1:要求 的长度
可以先作出距离PQ,求出Q点坐标
利用两点的距离公式可以求
的长度.
解题步骤按:先求直线PQ方程,再求Q点
坐标,再求 的长度进行.(直接法)
问题探究3:如何求点到直线的距离?
相对而言 和 好求一些.
解题步骤:先作平行线得点R、S;再求R、S的坐标;
再求 的长;再由三角形的面积公式求 .
(面积法)
分析2:如果 垂直坐标
轴,则交点和距离都容易求出,
那么不妨做出与坐标轴垂直的线
段 和 ,如图所示,显然
已知点P的坐标为(x0, y0),直线l 的方程
是 Ax+B y +C=0,怎样求点P到直线l 的距离?
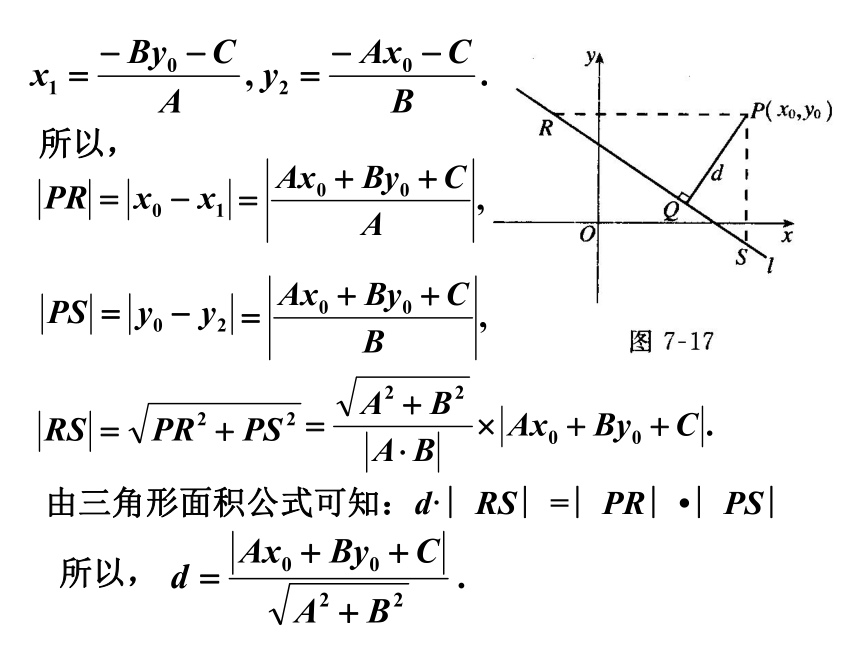
设A≠0,B≠0,这时l与x轴、y轴都相交。过P 作x轴的平行线,交l于点 R(x1, y0) ;作y轴的平行线,交l于点 S(x0, y2).
由 A x1+B y0 +C=0
A x0+B y2 +C=0
点到直线的距离公式的推导:
得
由三角形面积公式可知:d·∣RS∣=∣PR∣?∣PS∣
所以,
可证,当A=0或B=0时,以上公式仍适用。于是得到距离公式:
注意:先把直线方程化为一般式,再用公式 .
例1 求点P0(-1, 2)到下列直线的距离
(1) 2 x+ y -10=0; (2) 3 x=2.
教材108练习:
1. 求原点到下列直线的距离:
2. 求下列点到直线的距离:
例2、 已知点A(1,3),B(3,1),
C(– 1,0),求三角形ABC的面积。
解:设AB边上的高为h,则S△ABC =
AB边上的高h就是点C到AB的距离
AB边所在直线方程为x + y – 4 = 0。
所以点C到直线AB的距离,因此,S△ABC =
。
请同学们思考:本题还有其它解法吗?
问题探究4:
如何求两平行线间的距离?
能不能利用以上学过的点到直线的
距离公式呢?
如果能,怎么运用?
例2 求平行直线 2x-7y +8=0和 2x-7y -6=0的距离.
想一想:
再想一想:
注意:两直线的一次项系数完全相同,若不同,需变成系数完全相同时再用.
(教材110页B组3题)
已知点P的坐标为(x0, y0),直线l 的方程
是Ax+B y +C=0,则点P到直线l 的距离为:
小结:1.点到直线的距离公式:
2.平行线间的距离公式:
则
课后作业
2. 预习113的小结并做114的复习参考题A组.
1. 教材第109页 习题 3.3 A组 6~10
高中数学人教A版必修2
复习回顾:
平面几何中研究了几种距离,该怎样计算
点到点的距离
点到线的距离
两平行线间的距离
问题1:如何求点P (– 1 , 2) 到直线l:3x = 2的距离?
问题2:如何求原点O到直线l:3x + 2y – 26 = 0的离?
问题探究3:如何求点到直线的距离?
直线 的距离.
( 不在直线 上,且 , ),试求 点到
已知: 和直线 :
分析1:要求 的长度
可以先作出距离PQ,求出Q点坐标
利用两点的距离公式可以求
的长度.
解题步骤按:先求直线PQ方程,再求Q点
坐标,再求 的长度进行.(直接法)
问题探究3:如何求点到直线的距离?
相对而言 和 好求一些.
解题步骤:先作平行线得点R、S;再求R、S的坐标;
再求 的长;再由三角形的面积公式求 .
(面积法)
分析2:如果 垂直坐标
轴,则交点和距离都容易求出,
那么不妨做出与坐标轴垂直的线
段 和 ,如图所示,显然
已知点P的坐标为(x0, y0),直线l 的方程
是 Ax+B y +C=0,怎样求点P到直线l 的距离?
设A≠0,B≠0,这时l与x轴、y轴都相交。过P 作x轴的平行线,交l于点 R(x1, y0) ;作y轴的平行线,交l于点 S(x0, y2).
由 A x1+B y0 +C=0
A x0+B y2 +C=0
点到直线的距离公式的推导:
得
由三角形面积公式可知:d·∣RS∣=∣PR∣?∣PS∣
所以,
可证,当A=0或B=0时,以上公式仍适用。于是得到距离公式:
注意:先把直线方程化为一般式,再用公式 .
例1 求点P0(-1, 2)到下列直线的距离
(1) 2 x+ y -10=0; (2) 3 x=2.
教材108练习:
1. 求原点到下列直线的距离:
2. 求下列点到直线的距离:
例2、 已知点A(1,3),B(3,1),
C(– 1,0),求三角形ABC的面积。
解:设AB边上的高为h,则S△ABC =
AB边上的高h就是点C到AB的距离
AB边所在直线方程为x + y – 4 = 0。
所以点C到直线AB的距离,因此,S△ABC =
。
请同学们思考:本题还有其它解法吗?
问题探究4:
如何求两平行线间的距离?
能不能利用以上学过的点到直线的
距离公式呢?
如果能,怎么运用?
例2 求平行直线 2x-7y +8=0和 2x-7y -6=0的距离.
想一想:
再想一想:
注意:两直线的一次项系数完全相同,若不同,需变成系数完全相同时再用.
(教材110页B组3题)
已知点P的坐标为(x0, y0),直线l 的方程
是Ax+B y +C=0,则点P到直线l 的距离为:
小结:1.点到直线的距离公式:
2.平行线间的距离公式:
则
课后作业
2. 预习113的小结并做114的复习参考题A组.
1. 教材第109页 习题 3.3 A组 6~10
