山东省昌邑市第一中学人教版高中数学必修二课件:1.1.7 柱、锥、台和球体的体积(共38张PPT)
文档属性
| 名称 | 山东省昌邑市第一中学人教版高中数学必修二课件:1.1.7 柱、锥、台和球体的体积(共38张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-12 09:04:32 | ||
图片预览








文档简介
1.1.7柱、锥、台和球体的体积
学习目标
1.了解祖暅原理及等体积变换的意义.
2.掌握柱、锥、台、球的体积公式并会求它们的体积.
复习回顾
1.正方体的体积公式
V正方体=a3(这里a为棱长)
2.长方体的体积公式
V长方体=abc(这里a,b,c分别为长方体长、宽、高)
或V长方体=sh(s,h分别表示长方体的底面积和高)
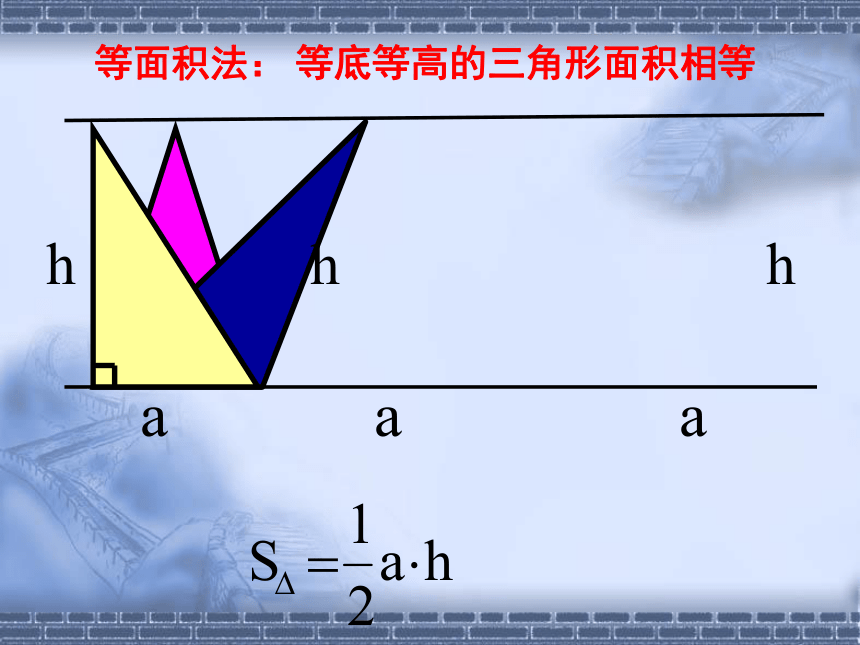
等底等高的三角形面积相等
等面积法:
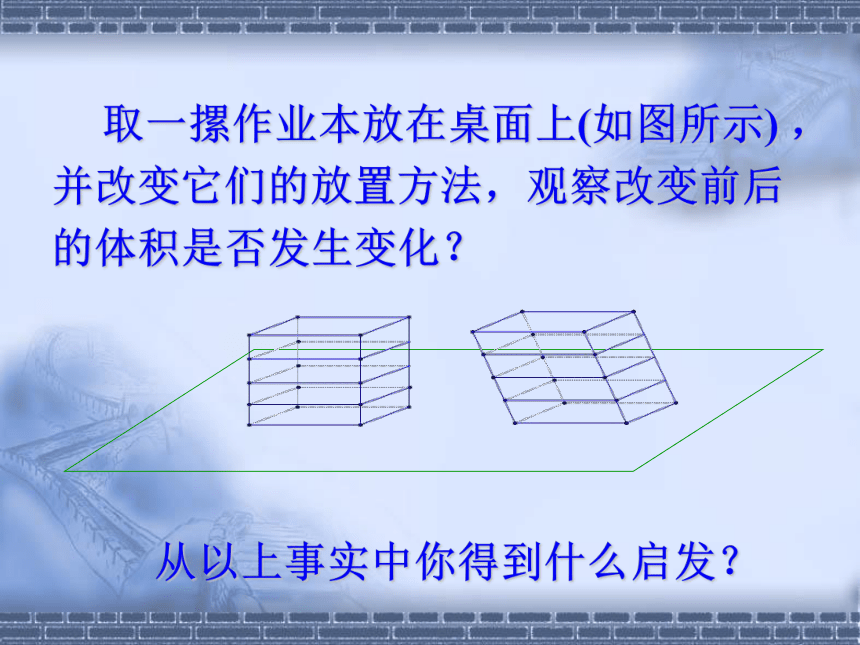
取一摞作业本放在桌面上(如图所示) ,并改变它们的放置方法,观察改变前后的体积是否发生变化?
从以上事实中你得到什么启发?
一. 祖暅原理
祖暅原理:幂势既同,则积不容异.
也就是说,夹在两个平行平面间的两个几何体,被平行于这两个平面的任意平面所截,如果截得的两个截面的面积总相等,那么这两个几何体的体积相等.
祖暅原理是推导柱、锥、台和球体积公式的基础和纽带,原理中含有三个条件,
条件一是两个几何体夹在两个平行平面之间;
条件二是用平行于两个平行平面的任何一平面可截得两个平面;
条件三是两个截面的面积总相等,这三个条件缺一不可,否则结论不成立.
祖冲之( 公元429年─公元500年)是我国杰出的数学家,科学家。南北朝时期人,汉族人,字文远。生于宋文帝元嘉六年,卒于齐昏侯永元二年。其主要贡献在数学、天文历法和机械三方面。
祖暅,祖冲之之子,圆满解决了球面积的计算问题,得到正确的体积公式。祖暅总结了刘徽的有关工作,提出“幂势既同则积不容异”,即等高的两立体,若其任意高处的水平截面积相等,则这两立体体积相等,这就是著名的“祖暅原理” (或刘祖原理)。祖暅应用这个原理,解决了刘徽尚未解决的球体积公式。该原理在西方直到十七世纪才由意大利数学家卡瓦列利发现,比祖暅晚一千一百多年。祖暅的儿子祖皓,续传家学,后来也成了数学家。
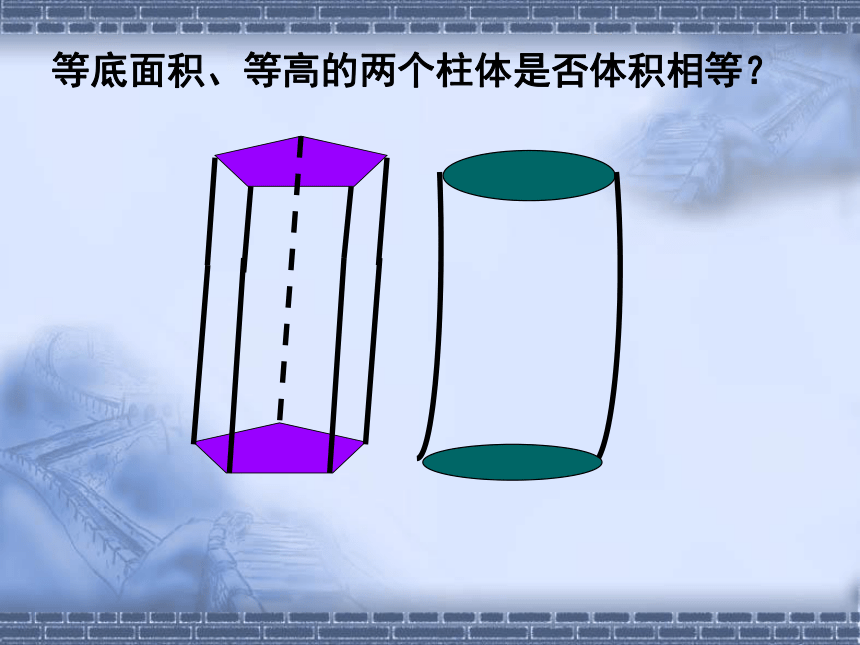
等底面积、等高的两个柱体是否体积相等?
体积相等
等高、等截面面积(不受截面形状影响)
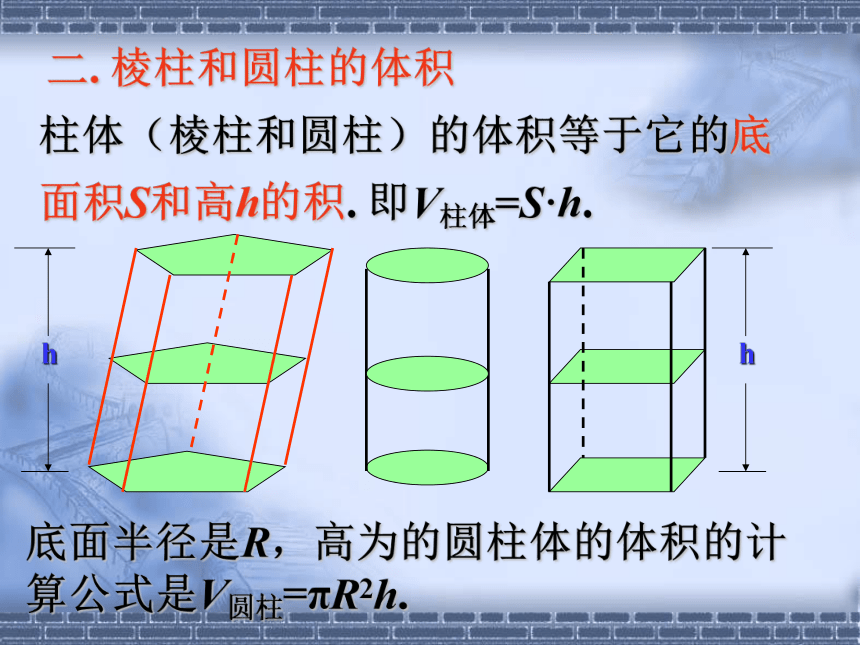
二. 棱柱和圆柱的体积
柱体(棱柱和圆柱)的体积等于它的底面积S和高h的积. 即V柱体=S·h.
h
h
底面半径是R,高为的圆柱体的体积的计算公式是V圆柱=πR2h.
将一个三棱柱按如图所示分解成三个三棱锥,那么这三个三棱锥的体积有什么关系?它们与三棱柱的体积有什么关系?
1
2
3
1
2
3
三. 棱锥和圆锥的体积
1. 如果一个锥体(棱锥、圆锥)的底面积是S,高是h,那么它的体积是V锥体= Sh.
2. 如果圆锥的底面半径是R,高是h,则它的体积是V圆锥= πR2h.
四. 棱台和圆台的体积
1. V台体= ;其中S、S’分别为台体上、下底面面积,h为台体的高.
2.V圆台=π(r2+Rr+R2)h,其中r、R分别为圆台的上、下底面的半径,高为h.
V柱体=sh
S=S/
S/ =0
S
S’
S
S
数
形
五. 球的体积
V球= ,其中R为球的半径.
实验:
给出如下几何模型
R
R
球的体积证明:
步骤
1.拿出圆锥
和圆柱
2.将圆锥倒立放入圆柱
结论:截面面积相等
R
则两个几何体的体积相等
3.取出半球和新的几何体做它们的截面
R
R
R
=
5.球的体积计算公式:
R
S1
探究
球的表面积:
例1. 如图所示,在长方体ABCD-A’B’C’ D’中,用截面截下一个棱锥C-A’DD’,求棱锥C-A’DD’的体积与剩余部分的体积之比。
A
D
C
B
C/
D/
B/
A/
C
A/
D/
D
S
h
例1. 如图所示,在长方体ABCD-A’B’C’ D’中,用截面截下一个棱锥C-A’DD’,求棱锥C-A’DD’的体积与剩余部分的体积之比。
解:已知长方体可以看作是直四棱柱ADD’A’-BCC’B’。
设底面ADD’A’的面积是S,高为h,
则它的体积为 V=Sh.
因为棱锥C-A’DD’的底面面积是 S,高是h,
所以棱锥C-A’DD’的体积是
VC-A’DD’=
所以 棱锥C-A’DD’的体积与剩余部分的体积之比是1:5.
例2.有一堆规格相同的铁制(铁的密度是7.8g/cm3)六角螺帽共重5.8kg,已知螺帽底面是正六边形,边长为12mm,内孔直径为10mm,高为10mm,问这堆螺帽大约有多少个( 取3.14,可用计算器)?
解:六角螺帽的体积是六棱柱的体积与圆柱体积之差,
因此约有
5.8×103÷(7.8×2.956) ≈252(个)
答:螺帽的个数约为252个.
练习题:
1.设六正棱锥的底面边长为1,侧棱长为 ,那么它的体积为( )
(A)6 (B)
(C)2 (D)2
B
2.正棱锥的高和底面边长都缩小原来的 ,则它的体积是原来的( )
(A) (B)
(C) (D)
B
3.直三棱柱ABC-A1B1C1的体积为V,已知点P、Q分别为AA1、CC1上的点,而且满足AP=C1Q,则四棱锥B-APQC 的体积是( )
(A) (B)
(C) (D)
B
4.把一个大金属球表面涂漆,需油漆2.4kg,若把这个金属球熔化,制成64个半径相等的小金属球(设损耗为零),将这些小金属球表面涂漆,需用油漆 kg.
9.6
5.已知圆锥的母线长为8,底面周长为6π,则它的体积是 .
6.一个正方体的所有顶点都在球面上,若这个球的体积是V,则这个正方体的体积是 .
7. 若球的大圆面积扩大为原来的3倍,则它的 体积扩大为原来的( )
(A)3倍 (B)9倍
(C)27倍 (D)3 倍
D
8. 圆台的上、下底面半径和高的比为1:4:4,母线长10,则圆台的体积为( )
(A)672π (B)224π
(C)100π (D)
B
祖暅原理
柱、锥、台的体积
小结
1.本节主要在学习了柱,锥,台及球体的体积和球的表面积.
2.应用上述结论解决实际问题.
作业:P32习题A6,7,8,9,10
学习目标
1.了解祖暅原理及等体积变换的意义.
2.掌握柱、锥、台、球的体积公式并会求它们的体积.
复习回顾
1.正方体的体积公式
V正方体=a3(这里a为棱长)
2.长方体的体积公式
V长方体=abc(这里a,b,c分别为长方体长、宽、高)
或V长方体=sh(s,h分别表示长方体的底面积和高)
等底等高的三角形面积相等
等面积法:
取一摞作业本放在桌面上(如图所示) ,并改变它们的放置方法,观察改变前后的体积是否发生变化?
从以上事实中你得到什么启发?
一. 祖暅原理
祖暅原理:幂势既同,则积不容异.
也就是说,夹在两个平行平面间的两个几何体,被平行于这两个平面的任意平面所截,如果截得的两个截面的面积总相等,那么这两个几何体的体积相等.
祖暅原理是推导柱、锥、台和球体积公式的基础和纽带,原理中含有三个条件,
条件一是两个几何体夹在两个平行平面之间;
条件二是用平行于两个平行平面的任何一平面可截得两个平面;
条件三是两个截面的面积总相等,这三个条件缺一不可,否则结论不成立.
祖冲之( 公元429年─公元500年)是我国杰出的数学家,科学家。南北朝时期人,汉族人,字文远。生于宋文帝元嘉六年,卒于齐昏侯永元二年。其主要贡献在数学、天文历法和机械三方面。
祖暅,祖冲之之子,圆满解决了球面积的计算问题,得到正确的体积公式。祖暅总结了刘徽的有关工作,提出“幂势既同则积不容异”,即等高的两立体,若其任意高处的水平截面积相等,则这两立体体积相等,这就是著名的“祖暅原理” (或刘祖原理)。祖暅应用这个原理,解决了刘徽尚未解决的球体积公式。该原理在西方直到十七世纪才由意大利数学家卡瓦列利发现,比祖暅晚一千一百多年。祖暅的儿子祖皓,续传家学,后来也成了数学家。
等底面积、等高的两个柱体是否体积相等?
体积相等
等高、等截面面积(不受截面形状影响)
二. 棱柱和圆柱的体积
柱体(棱柱和圆柱)的体积等于它的底面积S和高h的积. 即V柱体=S·h.
h
h
底面半径是R,高为的圆柱体的体积的计算公式是V圆柱=πR2h.
将一个三棱柱按如图所示分解成三个三棱锥,那么这三个三棱锥的体积有什么关系?它们与三棱柱的体积有什么关系?
1
2
3
1
2
3
三. 棱锥和圆锥的体积
1. 如果一个锥体(棱锥、圆锥)的底面积是S,高是h,那么它的体积是V锥体= Sh.
2. 如果圆锥的底面半径是R,高是h,则它的体积是V圆锥= πR2h.
四. 棱台和圆台的体积
1. V台体= ;其中S、S’分别为台体上、下底面面积,h为台体的高.
2.V圆台=π(r2+Rr+R2)h,其中r、R分别为圆台的上、下底面的半径,高为h.
V柱体=sh
S=S/
S/ =0
S
S’
S
S
数
形
五. 球的体积
V球= ,其中R为球的半径.
实验:
给出如下几何模型
R
R
球的体积证明:
步骤
1.拿出圆锥
和圆柱
2.将圆锥倒立放入圆柱
结论:截面面积相等
R
则两个几何体的体积相等
3.取出半球和新的几何体做它们的截面
R
R
R
=
5.球的体积计算公式:
R
S1
探究
球的表面积:
例1. 如图所示,在长方体ABCD-A’B’C’ D’中,用截面截下一个棱锥C-A’DD’,求棱锥C-A’DD’的体积与剩余部分的体积之比。
A
D
C
B
C/
D/
B/
A/
C
A/
D/
D
S
h
例1. 如图所示,在长方体ABCD-A’B’C’ D’中,用截面截下一个棱锥C-A’DD’,求棱锥C-A’DD’的体积与剩余部分的体积之比。
解:已知长方体可以看作是直四棱柱ADD’A’-BCC’B’。
设底面ADD’A’的面积是S,高为h,
则它的体积为 V=Sh.
因为棱锥C-A’DD’的底面面积是 S,高是h,
所以棱锥C-A’DD’的体积是
VC-A’DD’=
所以 棱锥C-A’DD’的体积与剩余部分的体积之比是1:5.
例2.有一堆规格相同的铁制(铁的密度是7.8g/cm3)六角螺帽共重5.8kg,已知螺帽底面是正六边形,边长为12mm,内孔直径为10mm,高为10mm,问这堆螺帽大约有多少个( 取3.14,可用计算器)?
解:六角螺帽的体积是六棱柱的体积与圆柱体积之差,
因此约有
5.8×103÷(7.8×2.956) ≈252(个)
答:螺帽的个数约为252个.
练习题:
1.设六正棱锥的底面边长为1,侧棱长为 ,那么它的体积为( )
(A)6 (B)
(C)2 (D)2
B
2.正棱锥的高和底面边长都缩小原来的 ,则它的体积是原来的( )
(A) (B)
(C) (D)
B
3.直三棱柱ABC-A1B1C1的体积为V,已知点P、Q分别为AA1、CC1上的点,而且满足AP=C1Q,则四棱锥B-APQC 的体积是( )
(A) (B)
(C) (D)
B
4.把一个大金属球表面涂漆,需油漆2.4kg,若把这个金属球熔化,制成64个半径相等的小金属球(设损耗为零),将这些小金属球表面涂漆,需用油漆 kg.
9.6
5.已知圆锥的母线长为8,底面周长为6π,则它的体积是 .
6.一个正方体的所有顶点都在球面上,若这个球的体积是V,则这个正方体的体积是 .
7. 若球的大圆面积扩大为原来的3倍,则它的 体积扩大为原来的( )
(A)3倍 (B)9倍
(C)27倍 (D)3 倍
D
8. 圆台的上、下底面半径和高的比为1:4:4,母线长10,则圆台的体积为( )
(A)672π (B)224π
(C)100π (D)
B
祖暅原理
柱、锥、台的体积
小结
1.本节主要在学习了柱,锥,台及球体的体积和球的表面积.
2.应用上述结论解决实际问题.
作业:P32习题A6,7,8,9,10
