勾股定理应用举例
图片预览

文档简介
(共10张PPT)
利用勾股定理
求解几何体的最短路线长
A
B
我怎么走
会最近呢
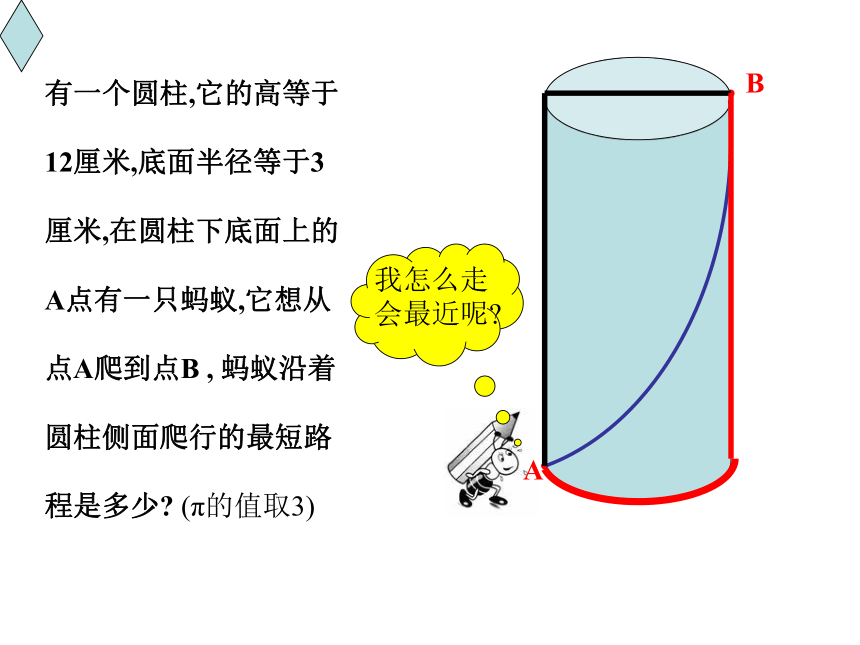
有一个圆柱,它的高等于
12厘米,底面半径等于3
厘米,在圆柱下底面上的
A点有一只蚂蚁,它想从
点A爬到点B , 蚂蚁沿着
圆柱侧面爬行的最短路
程是多少 (π的值取3)
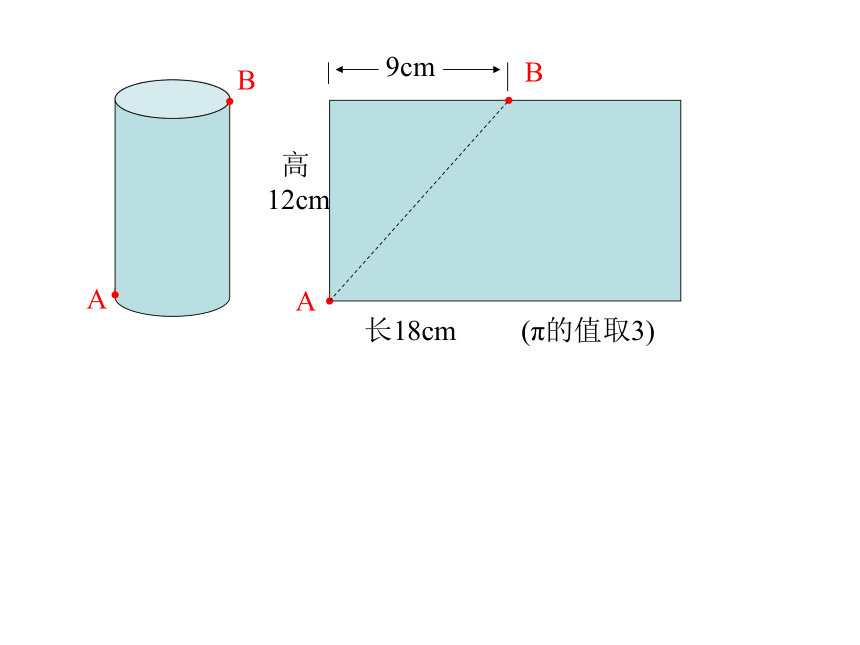
B
A
高
12cm
B
A
长18cm (π的值取3)
9cm
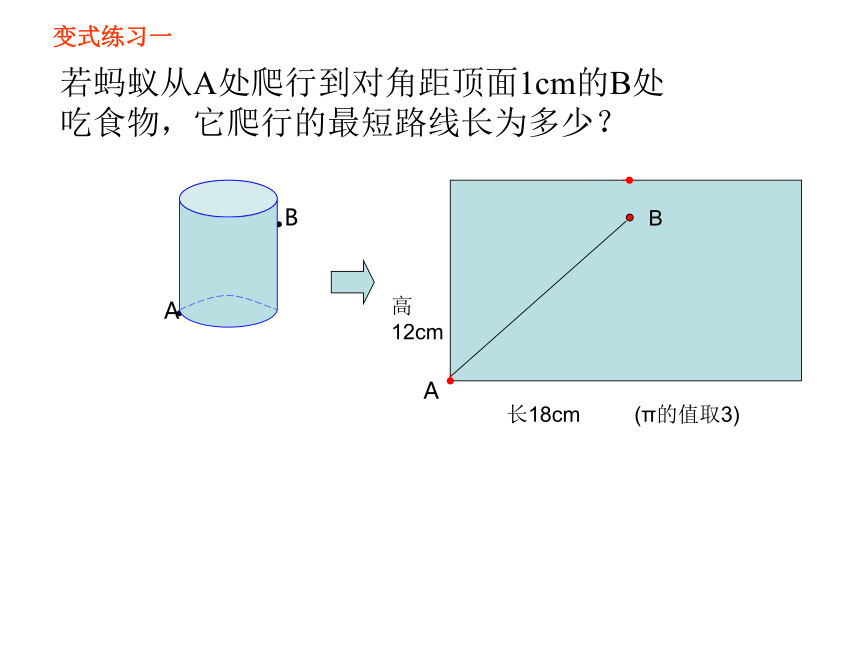
变式练习一
若蚂蚁从A处爬行到对角距顶面1cm的B处
吃食物,它爬行的最短路线长为多少?
A
B
高
12cm
长18cm (π的值取3)
A
B
A
B
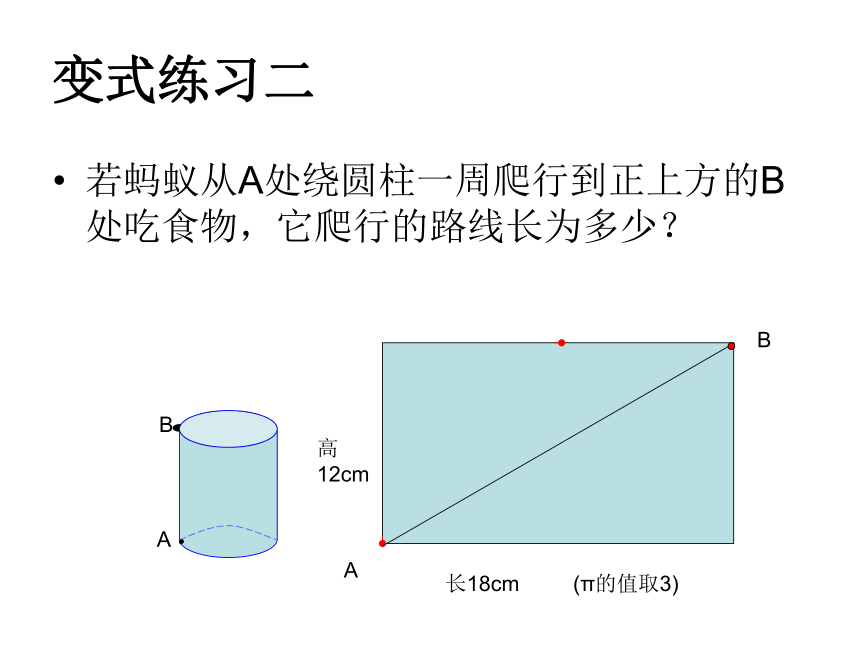
若蚂蚁从A处绕圆柱一周爬行到正上方的B处吃食物,它爬行的路线长为多少?
变式练习二
高
12cm
长18cm (π的值取3)
A
B
A
B
B
例 如图,一只蚂蚁从实心长方体的顶点A出发,沿长方体的表面爬到对角顶点C1处(三条棱长如图所示),问怎样走路线最短?最短路线长为多少?
A
B
A1
B1
D
C
D1
C1
2
1
4
A
B
D
C
D1
C1
①
4
2
1
②
A
B
B1
C
A1
C1
4
1
2
A
B1
D1
D
A1
C1
③
4
1
2
长方体中的最值问题
例 如图,是一个三级台阶,它的每一级的长、宽和高分别等于5cm,3cm和1cm,A和B是这个台阶的两个相对的端点,A点上有一只蚂蚁,想到B点去吃可口的食物.请你想一想,这只蚂蚁从A点出发,沿着台阶面爬到B点,最短线路是多少?
B
A
A
B
C
5
3
1
5
12
台阶中的最值问题
小 结:
把几何体适当展开成平面图形,再利用“两点之间线段最短”,或点到直线“垂线段最短”等性质找出最短距离,构造直角三角形,运用勾股定理解决问题。
随堂小测
1.有一只蚂蚁从一个矩形的顶点A 沿表面爬到顶点C,如果底面是一个边长为4厘米的正方形,高为6厘米,则蚂蚁所爬的最短路径是多少厘米?
A
C
利用勾股定理
求解几何体的最短路线长
A
B
我怎么走
会最近呢
有一个圆柱,它的高等于
12厘米,底面半径等于3
厘米,在圆柱下底面上的
A点有一只蚂蚁,它想从
点A爬到点B , 蚂蚁沿着
圆柱侧面爬行的最短路
程是多少 (π的值取3)
B
A
高
12cm
B
A
长18cm (π的值取3)
9cm
变式练习一
若蚂蚁从A处爬行到对角距顶面1cm的B处
吃食物,它爬行的最短路线长为多少?
A
B
高
12cm
长18cm (π的值取3)
A
B
A
B
若蚂蚁从A处绕圆柱一周爬行到正上方的B处吃食物,它爬行的路线长为多少?
变式练习二
高
12cm
长18cm (π的值取3)
A
B
A
B
B
例 如图,一只蚂蚁从实心长方体的顶点A出发,沿长方体的表面爬到对角顶点C1处(三条棱长如图所示),问怎样走路线最短?最短路线长为多少?
A
B
A1
B1
D
C
D1
C1
2
1
4
A
B
D
C
D1
C1
①
4
2
1
②
A
B
B1
C
A1
C1
4
1
2
A
B1
D1
D
A1
C1
③
4
1
2
长方体中的最值问题
例 如图,是一个三级台阶,它的每一级的长、宽和高分别等于5cm,3cm和1cm,A和B是这个台阶的两个相对的端点,A点上有一只蚂蚁,想到B点去吃可口的食物.请你想一想,这只蚂蚁从A点出发,沿着台阶面爬到B点,最短线路是多少?
B
A
A
B
C
5
3
1
5
12
台阶中的最值问题
小 结:
把几何体适当展开成平面图形,再利用“两点之间线段最短”,或点到直线“垂线段最短”等性质找出最短距离,构造直角三角形,运用勾股定理解决问题。
随堂小测
1.有一只蚂蚁从一个矩形的顶点A 沿表面爬到顶点C,如果底面是一个边长为4厘米的正方形,高为6厘米,则蚂蚁所爬的最短路径是多少厘米?
A
C
