第15章 轴对称 本章复习 课件(共28张PPT)
文档属性
| 名称 | 第15章 轴对称 本章复习 课件(共28张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-10 00:00:00 | ||
图片预览





文档简介
(共28张PPT)
本章复习
第15章
轴对称
沪科版·八年级数学上册
上课课件
学习目标
【知识与技能】
1.理解轴对称与轴对称图形的概念,掌握轴对称的性质.
2.掌握线段的垂直平分线、角的平分线的性质及应用.
3.理解等腰三角形的性质并能够简单应用.
4.理解等边三角形的性质并能够简单应用.
【过程与方法】
初步体会从对称的角度欣赏设计简单的轴对称图案.
【情感与态度】
数形结合的思想及方程的思想都应引起广泛的重视和应用.
【教学重点】
重点是掌握线段的垂直平分线、角的平分线的性质、等腰三角形的性质及应用.
【教学难点】
难点是轴对称图形以及关于某条直线成轴对称的概念,等腰三角形的性质应用.
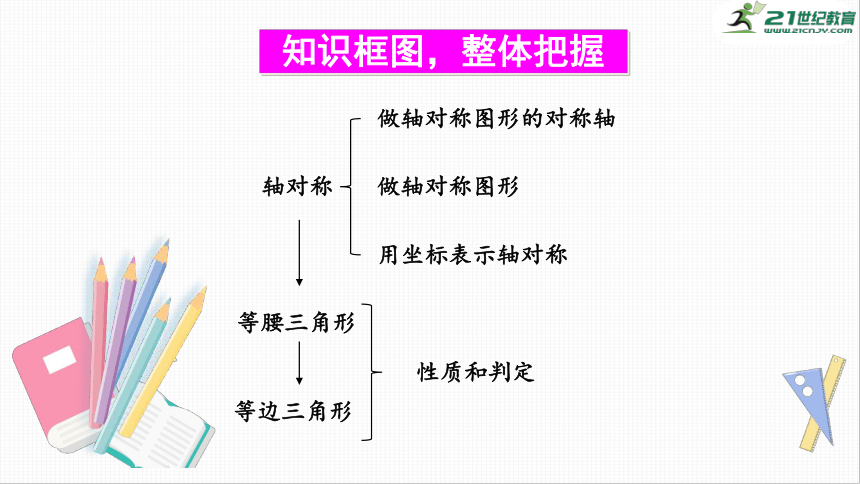
知识框图,整体把握
轴对称
做轴对称图形的对称轴
做轴对称图形
用坐标表示轴对称
等腰三角形
等边三角形
性质和判定
典例精讲
1.关于“轴对称图形”与“轴对称”的认识
例1
(1)下列几何图形中,①线段②角③直角三角形④半圆,其中一定是轴对称图形的有(
)
A.1个
B.2个
C.3个
D.4个
C
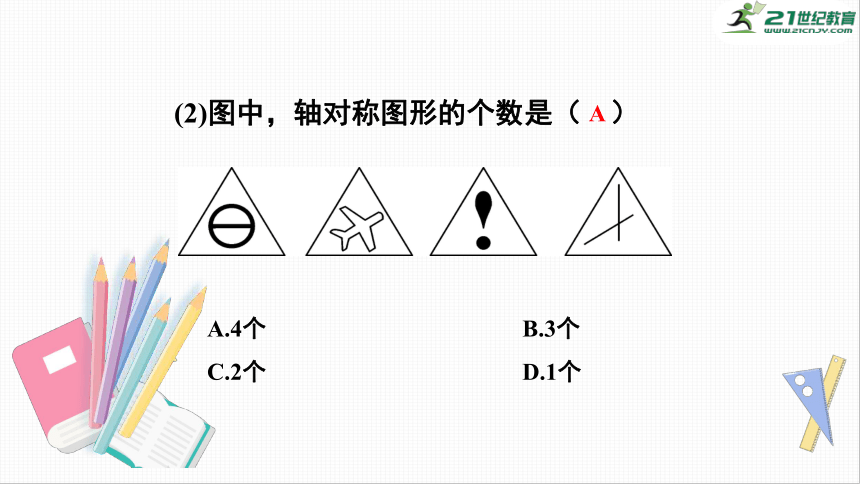
(2)图中,轴对称图形的个数是(
)
A
A.4个
B.3个
C.2个
D.1个
2.轴对称变换及用坐标表示轴对称
[关于坐标轴对称]
点P(x,y)关于x轴对称的点的坐标是(x,-y)
点P(x,y)关于y轴对称的点的坐标是(-x,y)
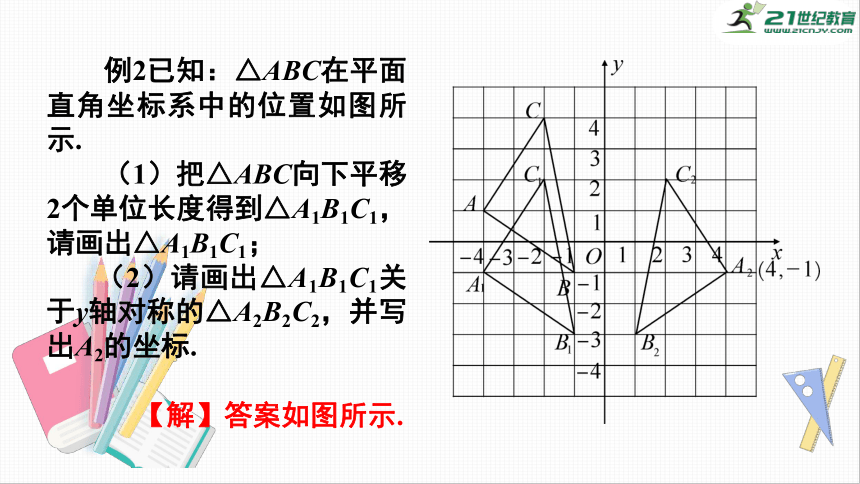
例2已知:△ABC在平面直角坐标系中的位置如图所示.
(1)把△ABC向下平移2个单位长度得到△A1B1C1,请画出△A1B1C1;
(2)请画出△A1B1C1关于y轴对称的△A2B2C2,并写出A2的坐标.
【解】答案如图所示.
3.作一个图形关于某条直线的轴对称图形
(1)作出一些关键点或特殊点的对称点.
(2)按原图形的连接方式连接所得到的对称点,即得到原图形的轴对称图形
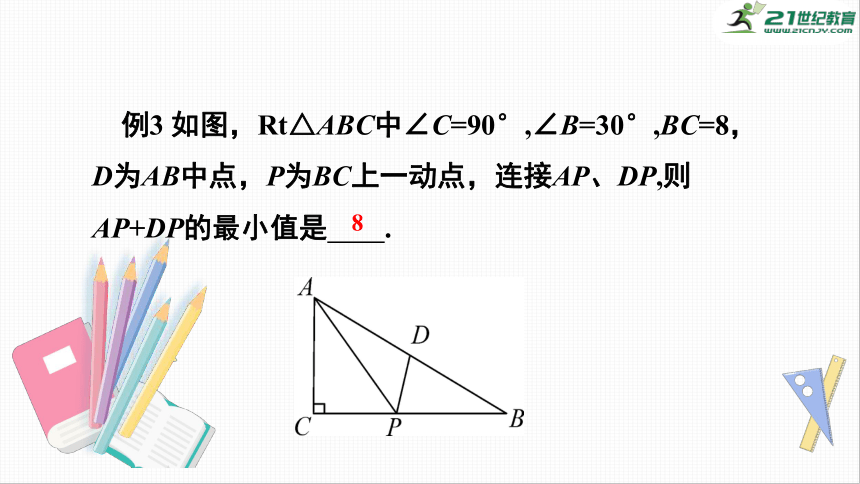
例3
如图,Rt△ABC中∠C=90°,∠B=30°,BC=8,D为AB中点,P为BC上一动点,连接AP、DP,则AP+DP的最小值是
.
8
4.线段垂直平分线的性质
例4如图,在△ABC中,∠A=90°,BD为∠ABC的平分线,DE⊥BC,E是BC的中点,求∠C的度数.
【解】∵在△ABC中,BD平分∠ABC,
∴∠ABD=∠CBD,
∵DE⊥BC,且E是BC的中点,∴BE=CE,
∴BD=CD,
∴∠DBC=∠C,
∴∠ABD=∠CBD=∠C,
∵∠ABD+∠CBD+∠C=90°,
∴∠ABD=∠CBD=∠C=30°.
5.等腰三角形的特征和识别
例5
已知:如图,△ABC中,∠ACB为锐角且平分线交AB于点E,EF∥BC交AC于点F,交∠ACB的外角平分线于点G.试判断△EFC的形状,并说明你的理由.
【解】△EFC为等腰三角形,
证明:∵CE平分∠ACB,
∴∠BCE=∠ACE,
∵EF∥BC,
∴∠FEC=∠BCE,
∠FEC=∠ACE(等量代换),
∴△EFC为等腰三角形
6.等边三角形的特征和识别
例6:如图,D、E、F分别是等边△ABC各边上的点,FE⊥BC,DF⊥AC,ED⊥AB,垂足分别为点E,F,D,求证:△DEF为等边三角形.
【解】∵△ABC为等边三角形,
∴∠A=∠B=∠C=60°,
∵DF⊥AC,
∴∠DFA=90°,
∴∠ADF=30°,
∵ED⊥AB,
∴∠BDE=90°,
∴∠FDE=180°-∠ADF-∠EDB=60°.
同理可得:∠DFE=60°,∠DEF=60°,
∴△DEF为等边三角形.
例7:如图,已知:在△ABC中,AB=AC,∠BAC=120°,AB的垂直平分线交AB于点E,交BC于点F.求证:CF=2BF.
【解】解:如图,连接AF,
∵AB=AC,∠BAC=120°,
∴∠B=∠C=30°,
∵EF垂直平分AB,
∴BF=AF,
∴∠B=∠FAB=30°,
∴∠FAC=∠BAC-∠FAB=90°,
∴CF=2AF,
∴CF=2BF.
知识巩固
1.以下图形有两条对称轴的是(
)
A.正六边形
B.长方形
C.等腰三角形
D.圆
B
2.如图,在△ABC中,AB=AC,点D在AC上,且BD=BC=AD,则∠A为______.
36°
3.如图,在△ABC中,DE是边AC的垂直平分线,若BC=8cm,AB=10cm,则△EBC的周长为______cm(学生可以合作讨论,互帮互学)
18
4.四边形ABCD是正方形,△PAD是等边三角形,求∠BPC的度数.
解:①若P点在正方形ABCD外部,
如图(1)所示,
∵△PAD为等边三角形,
∴PA=PD=AD,∠APD=∠PAD=∠PDA=60°,
∵四边形ABCD为正方形,
∴AB=AD=BC=CD,
∴PA=BA,则△PAB为等腰三角形,
∴∠PBA=∠APB.
又∵∠BAP=∠BAD+∠PAD=150°,
∴∠PBA=∠APB=15°,
同理可得∠CPD=15°,
∵∠BPC=∠APD-∠BPA-∠CPD,
∴∠BPC=30°.
②若点P在正方形ABCD内部,如图(2)所示,
∵△PAD为等边三角形
∴PA=PD=AD,
∠APD=∠PAD=∠PDA=60°,
∵四边形ABCD为正方形,
∴AB=AD=BC=CD,
∠BAD=∠ADC=∠DCB=∠CBA=90°,
∴∠BAP=30°,PA=BA,
∴△ABP为等腰三角形.
∴∠ABP=∠APB=75°,
∴∠PBC=15°.
同理可得:∠PCB=15°,
∴∠BPC=150°.
1.关于轴对称的点,线段,图形的性质与作法.
2.角平分线的性质.
3.垂直平分线的性质.
4.等腰三角形的性质与应用.
5.等边三角形的性质与应用.
课堂小结
1.从教材习题中选取完成练习;
2.完成练习册本课时的习题.
课后作业
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!
本章复习
第15章
轴对称
沪科版·八年级数学上册
上课课件
学习目标
【知识与技能】
1.理解轴对称与轴对称图形的概念,掌握轴对称的性质.
2.掌握线段的垂直平分线、角的平分线的性质及应用.
3.理解等腰三角形的性质并能够简单应用.
4.理解等边三角形的性质并能够简单应用.
【过程与方法】
初步体会从对称的角度欣赏设计简单的轴对称图案.
【情感与态度】
数形结合的思想及方程的思想都应引起广泛的重视和应用.
【教学重点】
重点是掌握线段的垂直平分线、角的平分线的性质、等腰三角形的性质及应用.
【教学难点】
难点是轴对称图形以及关于某条直线成轴对称的概念,等腰三角形的性质应用.
知识框图,整体把握
轴对称
做轴对称图形的对称轴
做轴对称图形
用坐标表示轴对称
等腰三角形
等边三角形
性质和判定
典例精讲
1.关于“轴对称图形”与“轴对称”的认识
例1
(1)下列几何图形中,①线段②角③直角三角形④半圆,其中一定是轴对称图形的有(
)
A.1个
B.2个
C.3个
D.4个
C
(2)图中,轴对称图形的个数是(
)
A
A.4个
B.3个
C.2个
D.1个
2.轴对称变换及用坐标表示轴对称
[关于坐标轴对称]
点P(x,y)关于x轴对称的点的坐标是(x,-y)
点P(x,y)关于y轴对称的点的坐标是(-x,y)
例2已知:△ABC在平面直角坐标系中的位置如图所示.
(1)把△ABC向下平移2个单位长度得到△A1B1C1,请画出△A1B1C1;
(2)请画出△A1B1C1关于y轴对称的△A2B2C2,并写出A2的坐标.
【解】答案如图所示.
3.作一个图形关于某条直线的轴对称图形
(1)作出一些关键点或特殊点的对称点.
(2)按原图形的连接方式连接所得到的对称点,即得到原图形的轴对称图形
例3
如图,Rt△ABC中∠C=90°,∠B=30°,BC=8,D为AB中点,P为BC上一动点,连接AP、DP,则AP+DP的最小值是
.
8
4.线段垂直平分线的性质
例4如图,在△ABC中,∠A=90°,BD为∠ABC的平分线,DE⊥BC,E是BC的中点,求∠C的度数.
【解】∵在△ABC中,BD平分∠ABC,
∴∠ABD=∠CBD,
∵DE⊥BC,且E是BC的中点,∴BE=CE,
∴BD=CD,
∴∠DBC=∠C,
∴∠ABD=∠CBD=∠C,
∵∠ABD+∠CBD+∠C=90°,
∴∠ABD=∠CBD=∠C=30°.
5.等腰三角形的特征和识别
例5
已知:如图,△ABC中,∠ACB为锐角且平分线交AB于点E,EF∥BC交AC于点F,交∠ACB的外角平分线于点G.试判断△EFC的形状,并说明你的理由.
【解】△EFC为等腰三角形,
证明:∵CE平分∠ACB,
∴∠BCE=∠ACE,
∵EF∥BC,
∴∠FEC=∠BCE,
∠FEC=∠ACE(等量代换),
∴△EFC为等腰三角形
6.等边三角形的特征和识别
例6:如图,D、E、F分别是等边△ABC各边上的点,FE⊥BC,DF⊥AC,ED⊥AB,垂足分别为点E,F,D,求证:△DEF为等边三角形.
【解】∵△ABC为等边三角形,
∴∠A=∠B=∠C=60°,
∵DF⊥AC,
∴∠DFA=90°,
∴∠ADF=30°,
∵ED⊥AB,
∴∠BDE=90°,
∴∠FDE=180°-∠ADF-∠EDB=60°.
同理可得:∠DFE=60°,∠DEF=60°,
∴△DEF为等边三角形.
例7:如图,已知:在△ABC中,AB=AC,∠BAC=120°,AB的垂直平分线交AB于点E,交BC于点F.求证:CF=2BF.
【解】解:如图,连接AF,
∵AB=AC,∠BAC=120°,
∴∠B=∠C=30°,
∵EF垂直平分AB,
∴BF=AF,
∴∠B=∠FAB=30°,
∴∠FAC=∠BAC-∠FAB=90°,
∴CF=2AF,
∴CF=2BF.
知识巩固
1.以下图形有两条对称轴的是(
)
A.正六边形
B.长方形
C.等腰三角形
D.圆
B
2.如图,在△ABC中,AB=AC,点D在AC上,且BD=BC=AD,则∠A为______.
36°
3.如图,在△ABC中,DE是边AC的垂直平分线,若BC=8cm,AB=10cm,则△EBC的周长为______cm(学生可以合作讨论,互帮互学)
18
4.四边形ABCD是正方形,△PAD是等边三角形,求∠BPC的度数.
解:①若P点在正方形ABCD外部,
如图(1)所示,
∵△PAD为等边三角形,
∴PA=PD=AD,∠APD=∠PAD=∠PDA=60°,
∵四边形ABCD为正方形,
∴AB=AD=BC=CD,
∴PA=BA,则△PAB为等腰三角形,
∴∠PBA=∠APB.
又∵∠BAP=∠BAD+∠PAD=150°,
∴∠PBA=∠APB=15°,
同理可得∠CPD=15°,
∵∠BPC=∠APD-∠BPA-∠CPD,
∴∠BPC=30°.
②若点P在正方形ABCD内部,如图(2)所示,
∵△PAD为等边三角形
∴PA=PD=AD,
∠APD=∠PAD=∠PDA=60°,
∵四边形ABCD为正方形,
∴AB=AD=BC=CD,
∠BAD=∠ADC=∠DCB=∠CBA=90°,
∴∠BAP=30°,PA=BA,
∴△ABP为等腰三角形.
∴∠ABP=∠APB=75°,
∴∠PBC=15°.
同理可得:∠PCB=15°,
∴∠BPC=150°.
1.关于轴对称的点,线段,图形的性质与作法.
2.角平分线的性质.
3.垂直平分线的性质.
4.等腰三角形的性质与应用.
5.等边三角形的性质与应用.
课堂小结
1.从教材习题中选取完成练习;
2.完成练习册本课时的习题.
课后作业
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!
