15.4角的平分线 第3课时 角平分线的判定 课件(共18张PPT)
文档属性
| 名称 | 15.4角的平分线 第3课时 角平分线的判定 课件(共18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-10 00:00:00 | ||
图片预览






文档简介
(共18张PPT)
第3课时
角平分线的判定
15.4
角的平分线
沪科版·八年级数学上册
上课课件
学习目标
【知识与技能】
探索角平分线的逆定理.
【过程与方法】
通过探索角平分线逆定理的过程,体会这个定理的作用,增强几何空间意识.
【情感与态度】
培养良好的逻辑推理能力.
【教学重点】
重点是掌握角平分线的逆定理.
【教学难点】
难点是运用角平分线定理简化证明线段相等的问题.
导入新知
写出上面角平分线性质定理的逆命题.
这逆命题是真命题吗?如果是真命题请写出已知、求证,并指出证明.
【归纳结论】角的内部到角两边距离相等的点在角的平分线上.
如图所示,PD⊥OA,PE⊥OB,PD=PE,则点P与∠AOB有什么特殊关系?
例1
如图,△ABC的角平分线BM,CN相交于点P,求证:点P到三边AB,BC,AC的距离相等.
证明:过点P作PD⊥AB,PE⊥BC,PF⊥AC,
垂足分别为D,E,F.
∵BM是△ABC的角平分线,点P在BM上,
∴PD=PE.同理,PE=PF.
∴PD=PE=PF,
即点P到三边AB,BC,CA的距离相等.
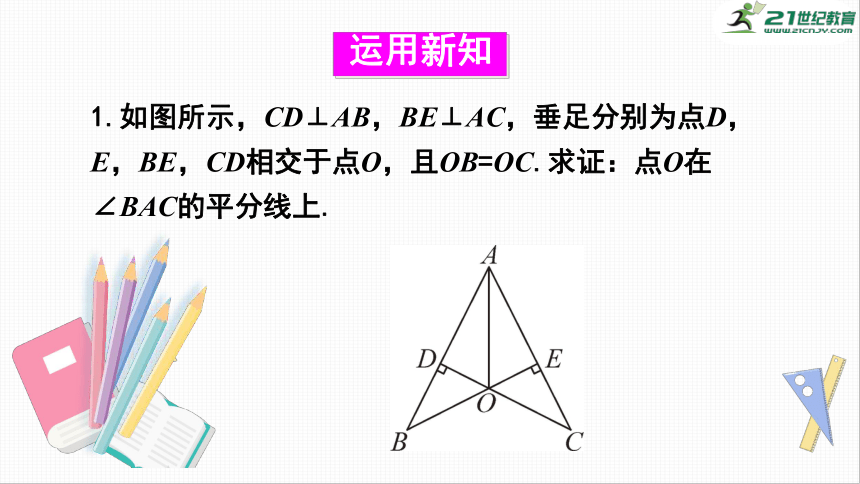
1.如图所示,CD⊥AB,BE⊥AC,垂足分别为点D,E,BE,CD相交于点O,且OB=OC.求证:点O在∠BAC的平分线上.
运用新知
证明:∵CD⊥AB,BE⊥AC,
∴∠BDO=∠CEO=90°.
又∵OB=OC,(已知)∠BOD=∠COE,(对顶角相等)
∴△BOD≌△COE(AAS)
∴OD=OE.
∴点O在∠BAC的平分线上.(角的内部到角两边距离相等的点在角的平分线上)
2.如图所示,OC平分∠AOB,P为OC上一点,PD⊥OA于点D,E为OA上一点,∠PEO+∠PFO=180°.求证:OE+OF=2OD.
证明:如图所示,过点P作PM⊥OB于点M.
∵OC平分∠AOB,PD⊥OA,(已知)
∴PD=PM.(角平分线上的点到角两边的距离相等)
在Rt△POD和Rt△POM中,
∴Rt△POD≌Rt△POM,(HL)
∴OD=OM.(全等三角形的对应边相等)
又∵∠PEO+∠PFO=180°,(已知)
∠PFM+∠PFO=180°,(平角定义)
∴∠PED=∠PFM.
又∵PD⊥OA,PM⊥OB,(已知)
∴∠PDE=∠PMF=90°.(垂直定义)
在△PDE和△PMF中,
∴△PDE≌△PMF,(AAS)
∴DE=MF,(全等三角形的对应边相等)
∴OE+OF=(OD+DE)+(OM-MF)=OD+DE+OD-DE=2OD.(等量代换)
随堂演练
1.如图,∠AOP=∠BOP=15°,PC∥OA,PD⊥OA,PC=4,则PD=(
)
C
A.4 B.3
C.2 D.1
2.到三角形三条边的距离都相等的点是这个三角形的(
)
A.三条中线的交点
B.三条高的交点
C.三条边的垂直平分线的交点
D.三条角平分线的交点
D
3.如图所示,已知BE⊥AC于E,CF⊥AB于F,BE、CF相交于点D,若BD=CD.求证:AD平分∠BAC.
证明:∵BE⊥AC,CF⊥AB,∴∠BFD=∠CED=90°.
又∵∠BDF=∠CDE,BD=CD,∴△BDF≌△CDE(AAS),
∴DF=DE,
∴点D在∠BAC平分线上,AD平分∠BAC.
1.这两个定理之间有何区别?
2.你还能得到哪些结论?
课堂小结
1.从教材习题中选取完成练习;
2.完成练习册本课时的习题.
课后作业
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!
第3课时
角平分线的判定
15.4
角的平分线
沪科版·八年级数学上册
上课课件
学习目标
【知识与技能】
探索角平分线的逆定理.
【过程与方法】
通过探索角平分线逆定理的过程,体会这个定理的作用,增强几何空间意识.
【情感与态度】
培养良好的逻辑推理能力.
【教学重点】
重点是掌握角平分线的逆定理.
【教学难点】
难点是运用角平分线定理简化证明线段相等的问题.
导入新知
写出上面角平分线性质定理的逆命题.
这逆命题是真命题吗?如果是真命题请写出已知、求证,并指出证明.
【归纳结论】角的内部到角两边距离相等的点在角的平分线上.
如图所示,PD⊥OA,PE⊥OB,PD=PE,则点P与∠AOB有什么特殊关系?
例1
如图,△ABC的角平分线BM,CN相交于点P,求证:点P到三边AB,BC,AC的距离相等.
证明:过点P作PD⊥AB,PE⊥BC,PF⊥AC,
垂足分别为D,E,F.
∵BM是△ABC的角平分线,点P在BM上,
∴PD=PE.同理,PE=PF.
∴PD=PE=PF,
即点P到三边AB,BC,CA的距离相等.
1.如图所示,CD⊥AB,BE⊥AC,垂足分别为点D,E,BE,CD相交于点O,且OB=OC.求证:点O在∠BAC的平分线上.
运用新知
证明:∵CD⊥AB,BE⊥AC,
∴∠BDO=∠CEO=90°.
又∵OB=OC,(已知)∠BOD=∠COE,(对顶角相等)
∴△BOD≌△COE(AAS)
∴OD=OE.
∴点O在∠BAC的平分线上.(角的内部到角两边距离相等的点在角的平分线上)
2.如图所示,OC平分∠AOB,P为OC上一点,PD⊥OA于点D,E为OA上一点,∠PEO+∠PFO=180°.求证:OE+OF=2OD.
证明:如图所示,过点P作PM⊥OB于点M.
∵OC平分∠AOB,PD⊥OA,(已知)
∴PD=PM.(角平分线上的点到角两边的距离相等)
在Rt△POD和Rt△POM中,
∴Rt△POD≌Rt△POM,(HL)
∴OD=OM.(全等三角形的对应边相等)
又∵∠PEO+∠PFO=180°,(已知)
∠PFM+∠PFO=180°,(平角定义)
∴∠PED=∠PFM.
又∵PD⊥OA,PM⊥OB,(已知)
∴∠PDE=∠PMF=90°.(垂直定义)
在△PDE和△PMF中,
∴△PDE≌△PMF,(AAS)
∴DE=MF,(全等三角形的对应边相等)
∴OE+OF=(OD+DE)+(OM-MF)=OD+DE+OD-DE=2OD.(等量代换)
随堂演练
1.如图,∠AOP=∠BOP=15°,PC∥OA,PD⊥OA,PC=4,则PD=(
)
C
A.4 B.3
C.2 D.1
2.到三角形三条边的距离都相等的点是这个三角形的(
)
A.三条中线的交点
B.三条高的交点
C.三条边的垂直平分线的交点
D.三条角平分线的交点
D
3.如图所示,已知BE⊥AC于E,CF⊥AB于F,BE、CF相交于点D,若BD=CD.求证:AD平分∠BAC.
证明:∵BE⊥AC,CF⊥AB,∴∠BFD=∠CED=90°.
又∵∠BDF=∠CDE,BD=CD,∴△BDF≌△CDE(AAS),
∴DF=DE,
∴点D在∠BAC平分线上,AD平分∠BAC.
1.这两个定理之间有何区别?
2.你还能得到哪些结论?
课堂小结
1.从教材习题中选取完成练习;
2.完成练习册本课时的习题.
课后作业
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!
