15.1轴对称图形 第3课时 平面直角坐标系中的轴对称 课件(共14张PPT)
文档属性
| 名称 | 15.1轴对称图形 第3课时 平面直角坐标系中的轴对称 课件(共14张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-10 00:00:00 | ||
图片预览





文档简介
(共14张PPT)
第3课时
平面直角坐标系中的轴对称
15.1
轴对称图形
沪科版·八年级数学上册
上课课件
学习目标
【知识与技能】
明确图形坐标变化与图形轴对称之间的关系.
【过程与方法】
经历图形坐标变化与图形轴对称之间关系的探索过程,明确图形坐标变化与图形轴对称之间的关系.
【情感与态度】
由坐标的变化探索新旧图形之间的变化过程,培养形象思维能力和数形结合意识.
【教学重点】
重点是图形坐标变化与图形轴对称之间的关系.
【教学难点】
难点是图形坐标变化规律的运用.
【思考】
在平面直角坐标系中,如何作出图形的轴对称图呢?
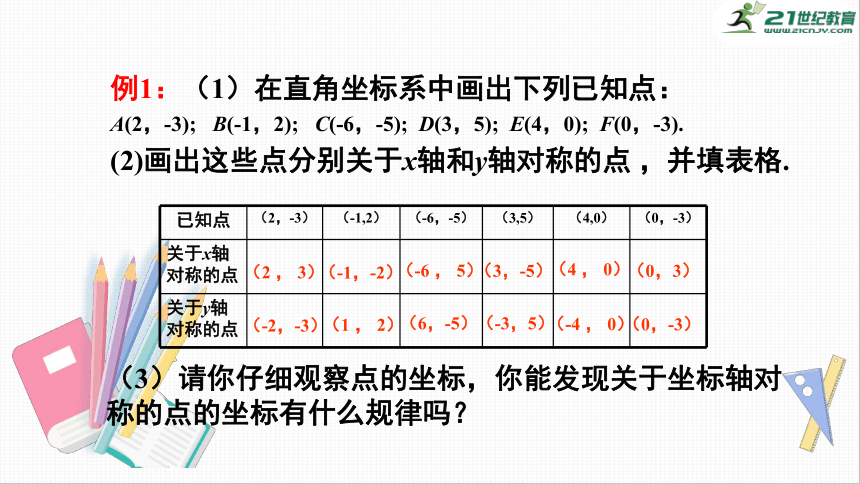
例1:(1)在直角坐标系中画出下列已知点:
A(2,-3);
B(-1,2);
C(-6,-5);
D(3,5);
E(4,0);
F(0,-3).
(2)画出这些点分别关于x轴和y轴对称的点
,并填表格.
已知点
(2,-3)
(-1,2)
(-6,-5)
(3,5)
(4,0)
(0,-3)
关于x轴对称的点
关于y轴对称的点
(2
,
3)
(-1,-2)
(-6
,
5)
(3,-5)
(4
,
0)
(0,3)
(-2,-3)
(1
,
2)
(6,-5)
(-3,5)
(-4
,
0)
(0,-3)
(3)请你仔细观察点的坐标,你能发现关于坐标轴对称的点的坐标有什么规律吗?
点(x,y)关于x轴对称的点的坐标为(x,-y),即横坐标相等,纵坐标互为相反数;
点(x,y)关于y轴对称的点的坐标为(-x,y),
即横坐标互为相反数,纵坐标相等.
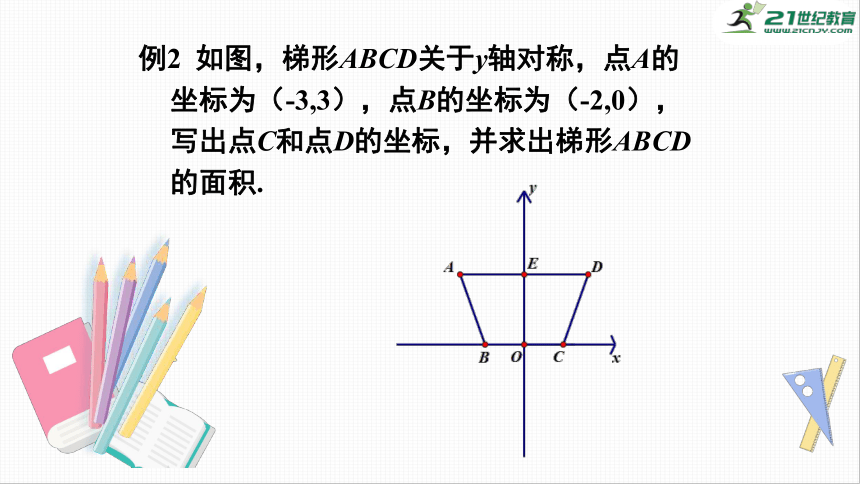
例2
如图,梯形ABCD关于y轴对称,点A的坐标为(-3,3),点B的坐标为(-2,0),写出点C和点D的坐标,并求出梯形ABCD的面积.
解:点D与点A(-3,3)关于y轴对称.
∴点D的坐标为(3.3).
同理点C的坐标为(2,0).
∴AD=|3-(-3)|=6,BC=|2-(-2)|=4.
∴S梯形=
随堂练习
1.如图,△ABC与△DEF关于y轴对称,已知A(-4,6),B(-6,2),E(2,1),则点D的坐标为(
)
A.(-4,6)
B.(4,6)
C.(-2,1)
D.(6,2)
B
2.已知点A(3,4),点A关于x轴对称的对称点A′的坐标为(
)
A.(3,4)
B.(3,-4)
C.(-3,-4)
D.(4,3)
B
3.已知P点关于x轴的对称点为P1,P1关于y轴的对称点为P2,已知P2的坐标为(5,-3),则点P的坐标为(
)
A.(5,3)
B.(-5,3)
C.(-5,-3)
D.(5,-3)
B
关于x轴和y轴对称的点
的坐标规律.
课堂小结
?点(x,y)关于x轴对称的点的坐标为(x,-y),即
横坐标相等,纵坐标互为相反数;
?点(x,y)关于y轴对称的点的坐标为(-x,y),即
横坐标互为相反数,纵坐标相等.
1.从教材习题中选取完成习题;
2.完成练习册本课时的习题.
课后作业
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!
第3课时
平面直角坐标系中的轴对称
15.1
轴对称图形
沪科版·八年级数学上册
上课课件
学习目标
【知识与技能】
明确图形坐标变化与图形轴对称之间的关系.
【过程与方法】
经历图形坐标变化与图形轴对称之间关系的探索过程,明确图形坐标变化与图形轴对称之间的关系.
【情感与态度】
由坐标的变化探索新旧图形之间的变化过程,培养形象思维能力和数形结合意识.
【教学重点】
重点是图形坐标变化与图形轴对称之间的关系.
【教学难点】
难点是图形坐标变化规律的运用.
【思考】
在平面直角坐标系中,如何作出图形的轴对称图呢?
例1:(1)在直角坐标系中画出下列已知点:
A(2,-3);
B(-1,2);
C(-6,-5);
D(3,5);
E(4,0);
F(0,-3).
(2)画出这些点分别关于x轴和y轴对称的点
,并填表格.
已知点
(2,-3)
(-1,2)
(-6,-5)
(3,5)
(4,0)
(0,-3)
关于x轴对称的点
关于y轴对称的点
(2
,
3)
(-1,-2)
(-6
,
5)
(3,-5)
(4
,
0)
(0,3)
(-2,-3)
(1
,
2)
(6,-5)
(-3,5)
(-4
,
0)
(0,-3)
(3)请你仔细观察点的坐标,你能发现关于坐标轴对称的点的坐标有什么规律吗?
点(x,y)关于x轴对称的点的坐标为(x,-y),即横坐标相等,纵坐标互为相反数;
点(x,y)关于y轴对称的点的坐标为(-x,y),
即横坐标互为相反数,纵坐标相等.
例2
如图,梯形ABCD关于y轴对称,点A的坐标为(-3,3),点B的坐标为(-2,0),写出点C和点D的坐标,并求出梯形ABCD的面积.
解:点D与点A(-3,3)关于y轴对称.
∴点D的坐标为(3.3).
同理点C的坐标为(2,0).
∴AD=|3-(-3)|=6,BC=|2-(-2)|=4.
∴S梯形=
随堂练习
1.如图,△ABC与△DEF关于y轴对称,已知A(-4,6),B(-6,2),E(2,1),则点D的坐标为(
)
A.(-4,6)
B.(4,6)
C.(-2,1)
D.(6,2)
B
2.已知点A(3,4),点A关于x轴对称的对称点A′的坐标为(
)
A.(3,4)
B.(3,-4)
C.(-3,-4)
D.(4,3)
B
3.已知P点关于x轴的对称点为P1,P1关于y轴的对称点为P2,已知P2的坐标为(5,-3),则点P的坐标为(
)
A.(5,3)
B.(-5,3)
C.(-5,-3)
D.(5,-3)
B
关于x轴和y轴对称的点
的坐标规律.
课堂小结
?点(x,y)关于x轴对称的点的坐标为(x,-y),即
横坐标相等,纵坐标互为相反数;
?点(x,y)关于y轴对称的点的坐标为(-x,y),即
横坐标互为相反数,纵坐标相等.
1.从教材习题中选取完成习题;
2.完成练习册本课时的习题.
课后作业
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!
