15.2 线段的垂直平分线 课件(共21张PPT)
文档属性
| 名称 | 15.2 线段的垂直平分线 课件(共21张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-10 06:48:12 | ||
图片预览




文档简介
(共21张PPT)
15.2
线段的垂直平分线
沪科版·八年级数学上册
上课课件
学习目标
【知识与技能】
掌握线段的垂直平分线以及它的逆定理的条件和结论,学会应用到证明中.
【过程与方法】
经历探索线段的垂直平分线定理、逆定理的过程,明确应用方法.
【情感与态度】
培养学生的合理推理能力.
【教学重点】
重点是线段的垂直平分线定理、逆定理的理解和应用.
【教学难点】
难点是线段的垂直平分线定理、逆定理的应用.
情景导入
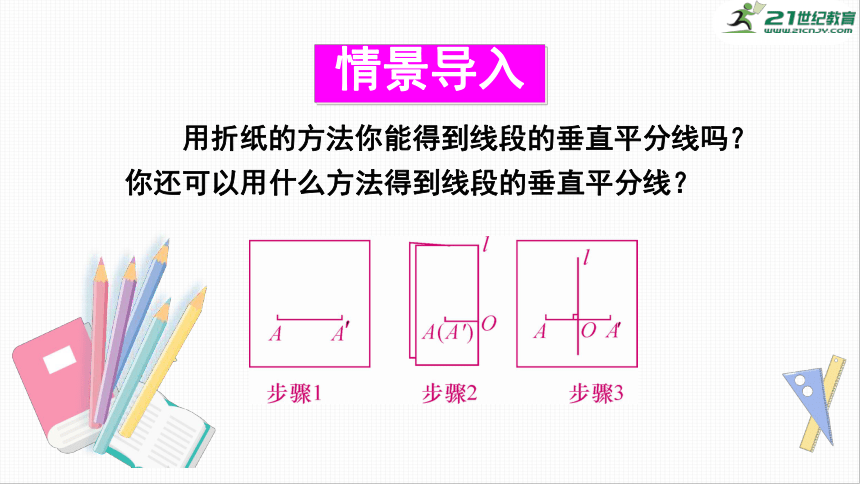
用折纸的方法你能得到线段的垂直平分线吗?你还可以用什么方法得到线段的垂直平分线?
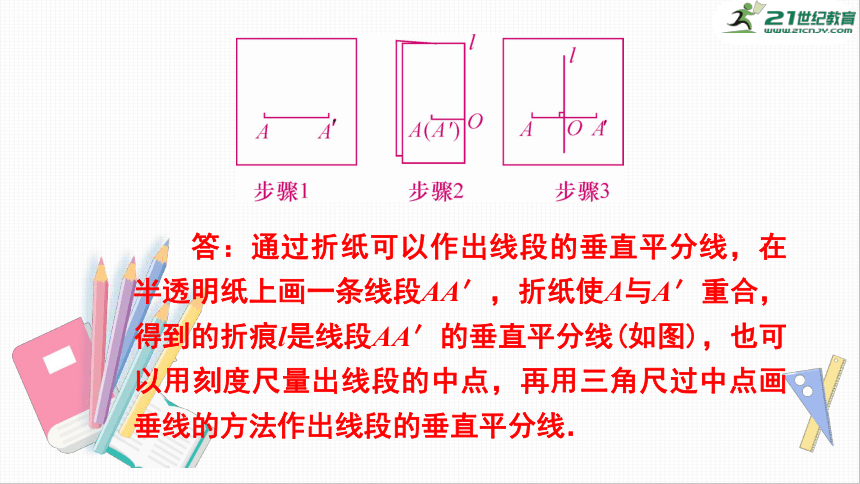
答:通过折纸可以作出线段的垂直平分线,在半透明纸上画一条线段AA′,折纸使A与A′重合,得到的折痕l是线段AA′的垂直平分线(如图),也可以用刻度尺量出线段的中点,再用三角尺过中点画垂线的方法作出线段的垂直平分线.
已知:线段AB,如图.
求作:线段AB的垂直平分线.
作法:
用尺规作线段的垂直平分线.
1.分别以点A,B为圆心,
大于
AB长为半径作弧,两弧交于点C和D.
A
B
C
D
2.
过点C,D作直线CD.
则直线CD就是线段AB的垂直平分线.
请你说明CD为什么是AB的垂直平分线,并与同伴进行交流.
注意:
因为直线CD与线段AB的交点就是AB的中点,所以我们也用这种方法作线段的中点.
A
B
PA=PB
P1
P1A=P1B
……
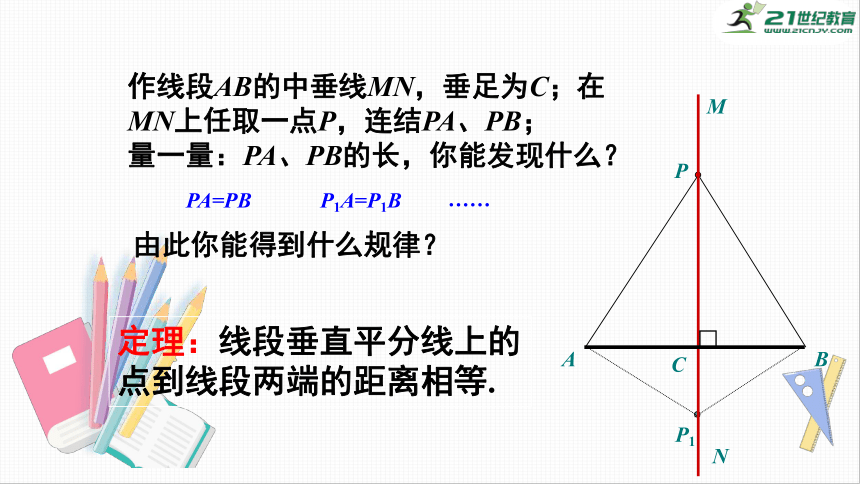
定理:线段垂直平分线上的点到线段两端的距离相等.
P
M
N
C
作线段AB的中垂线MN,垂足为C;在MN上任取一点P,连结PA、PB;
量一量:PA、PB的长,你能发现什么?
由此你能得到什么规律?
A
B
P
M
N
O
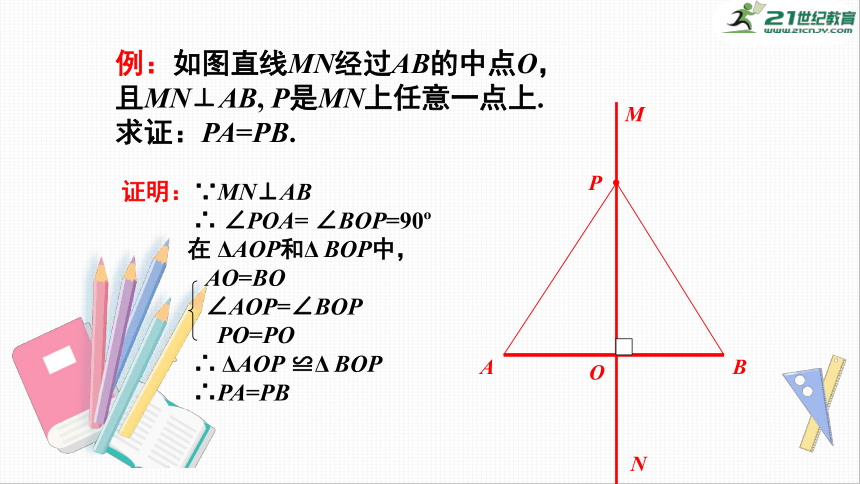
例:如图直线MN经过AB的中点O,且MN⊥AB,
P是MN上任意一点上.
求证:PA=PB.
证明:∵MN⊥AB
∴
∠POA=
∠BOP=90?
在
ΔAOP和Δ
BOP中,
AO=BO
∠AOP=∠BOP
PO=PO
∴
ΔAOP
≌Δ
BOP
∴PA=PB
探索发现
换一换:如果交换定理的题设和结论,会得到一个什么样的命题?它是真命题吗?
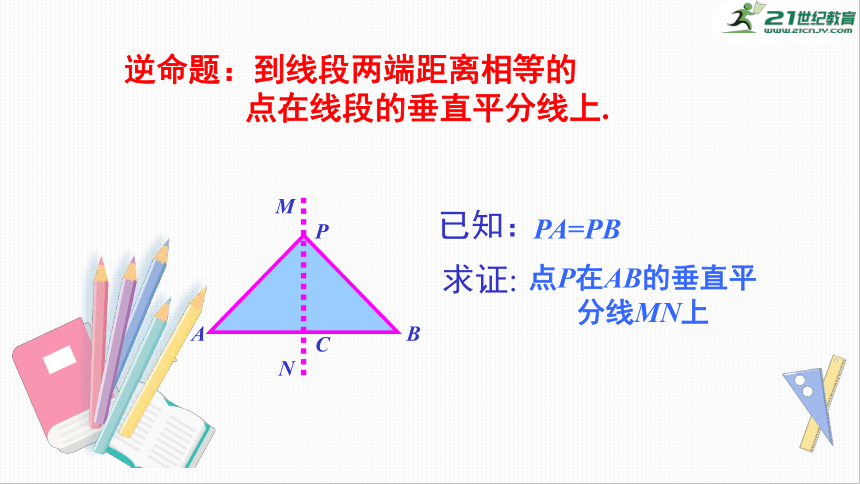
逆命题:到线段两端距离相等的
点在线段的垂直平分线上.
已知:
PA=PB
求证:
点P在AB的垂直平分线MN上
A
P
B
C
N
M
证明:(1)过P点画AB的垂线,交AB于点C.
P
A
B
C
M
N
(2)取AB中点C,过PC画直线MN
P
A
B
C
M
N
逆定理:到线段两端距离相等的点在
线段的垂直平分线上.
∵
PA=PB
∴
点P在AB的垂直平分线MN上
A
P
B
C
N
M
(已知)
(到线段两端距离相等的点在线段的垂直平分线上)
1.如图,直线CD是线段AB的垂直平分线,P为直线CD
上的一点,已知线段PA=5,则线段PB的长度为(
).
A.6
B.5
C.4
D.3
B
随堂练习
2.下列说法错误的是(
)
A.点D,E在线段AB垂直平分线上,则AD=BD,AE=BE
B.若AD=BD,AE=BE,则DE是线段AB的垂直平分线
C.若PA=PB,则点P在线段AB的垂直平分线上
D.若PA=PB,则过点P的直线是AB的垂直平分线
D
3.如图,OC是∠AOB的平分线,AC⊥AO,
BC⊥BO,则OC与AB的关系是(
).
A.
AB垂直平分OC
B.
OC垂直平分AB
C.
OC只平分AB但不平分
D.
OC只垂直AB但不平分
B
4.如图,△ABC中,AB=AC,∠A=36°,AC的垂直平分线交AB与E,D为垂足,连结EC.
(1)求∠ECD的度数;
(2)若CE=5,求BC的长.
解:(1)∵DE垂直平分AC,∴CE=AE,
∴∠ECD=∠A=36°.
(2)∵AB=AC,∠A=36°,
∴∠B=ACB=72°,
又∵∠ECD=36°,
∴∠BCE=∠ACB-∠ECD=36°,
∴∠BEC=72°=∠B,∴BC=EC=5.
本节课你学会了什么?有哪些收获?还有什么疑问?
课堂小结
1.从教材习题中选取完成习题;
2.完成练习册本课时的习题.
课后作业
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!
15.2
线段的垂直平分线
沪科版·八年级数学上册
上课课件
学习目标
【知识与技能】
掌握线段的垂直平分线以及它的逆定理的条件和结论,学会应用到证明中.
【过程与方法】
经历探索线段的垂直平分线定理、逆定理的过程,明确应用方法.
【情感与态度】
培养学生的合理推理能力.
【教学重点】
重点是线段的垂直平分线定理、逆定理的理解和应用.
【教学难点】
难点是线段的垂直平分线定理、逆定理的应用.
情景导入
用折纸的方法你能得到线段的垂直平分线吗?你还可以用什么方法得到线段的垂直平分线?
答:通过折纸可以作出线段的垂直平分线,在半透明纸上画一条线段AA′,折纸使A与A′重合,得到的折痕l是线段AA′的垂直平分线(如图),也可以用刻度尺量出线段的中点,再用三角尺过中点画垂线的方法作出线段的垂直平分线.
已知:线段AB,如图.
求作:线段AB的垂直平分线.
作法:
用尺规作线段的垂直平分线.
1.分别以点A,B为圆心,
大于
AB长为半径作弧,两弧交于点C和D.
A
B
C
D
2.
过点C,D作直线CD.
则直线CD就是线段AB的垂直平分线.
请你说明CD为什么是AB的垂直平分线,并与同伴进行交流.
注意:
因为直线CD与线段AB的交点就是AB的中点,所以我们也用这种方法作线段的中点.
A
B
PA=PB
P1
P1A=P1B
……
定理:线段垂直平分线上的点到线段两端的距离相等.
P
M
N
C
作线段AB的中垂线MN,垂足为C;在MN上任取一点P,连结PA、PB;
量一量:PA、PB的长,你能发现什么?
由此你能得到什么规律?
A
B
P
M
N
O
例:如图直线MN经过AB的中点O,且MN⊥AB,
P是MN上任意一点上.
求证:PA=PB.
证明:∵MN⊥AB
∴
∠POA=
∠BOP=90?
在
ΔAOP和Δ
BOP中,
AO=BO
∠AOP=∠BOP
PO=PO
∴
ΔAOP
≌Δ
BOP
∴PA=PB
探索发现
换一换:如果交换定理的题设和结论,会得到一个什么样的命题?它是真命题吗?
逆命题:到线段两端距离相等的
点在线段的垂直平分线上.
已知:
PA=PB
求证:
点P在AB的垂直平分线MN上
A
P
B
C
N
M
证明:(1)过P点画AB的垂线,交AB于点C.
P
A
B
C
M
N
(2)取AB中点C,过PC画直线MN
P
A
B
C
M
N
逆定理:到线段两端距离相等的点在
线段的垂直平分线上.
∵
PA=PB
∴
点P在AB的垂直平分线MN上
A
P
B
C
N
M
(已知)
(到线段两端距离相等的点在线段的垂直平分线上)
1.如图,直线CD是线段AB的垂直平分线,P为直线CD
上的一点,已知线段PA=5,则线段PB的长度为(
).
A.6
B.5
C.4
D.3
B
随堂练习
2.下列说法错误的是(
)
A.点D,E在线段AB垂直平分线上,则AD=BD,AE=BE
B.若AD=BD,AE=BE,则DE是线段AB的垂直平分线
C.若PA=PB,则点P在线段AB的垂直平分线上
D.若PA=PB,则过点P的直线是AB的垂直平分线
D
3.如图,OC是∠AOB的平分线,AC⊥AO,
BC⊥BO,则OC与AB的关系是(
).
A.
AB垂直平分OC
B.
OC垂直平分AB
C.
OC只平分AB但不平分
D.
OC只垂直AB但不平分
B
4.如图,△ABC中,AB=AC,∠A=36°,AC的垂直平分线交AB与E,D为垂足,连结EC.
(1)求∠ECD的度数;
(2)若CE=5,求BC的长.
解:(1)∵DE垂直平分AC,∴CE=AE,
∴∠ECD=∠A=36°.
(2)∵AB=AC,∠A=36°,
∴∠B=ACB=72°,
又∵∠ECD=36°,
∴∠BCE=∠ACB-∠ECD=36°,
∴∠BEC=72°=∠B,∴BC=EC=5.
本节课你学会了什么?有哪些收获?还有什么疑问?
课堂小结
1.从教材习题中选取完成习题;
2.完成练习册本课时的习题.
课后作业
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!
