15.3等腰三角形 第1课时 等腰三角形的性质 课件(共19张PPT)
文档属性
| 名称 | 15.3等腰三角形 第1课时 等腰三角形的性质 课件(共19张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-10 00:00:00 | ||
图片预览






文档简介
(共19张PPT)
15.3
等腰三角形
第1课时
等腰三角形的性质
沪科版·八年级数学上册
上课课件
学习目标
【知识与技能】
进一步认识等腰三角形的定义和性质.
【过程与方法】
通过观察、操作、想象、推理和交流活动,理解等腰三角形“三线合一”等有关性质、提高几何推理意识.
【情感与态度】
通过对问题的发现和解决,培养学生合作精神,树立学好教学的信心,形成有条理的表达.
【教学重点】
重点是掌握等腰三角形的性质.
【教学难点】
难点是对等腰三角形“三线合一”的理解.
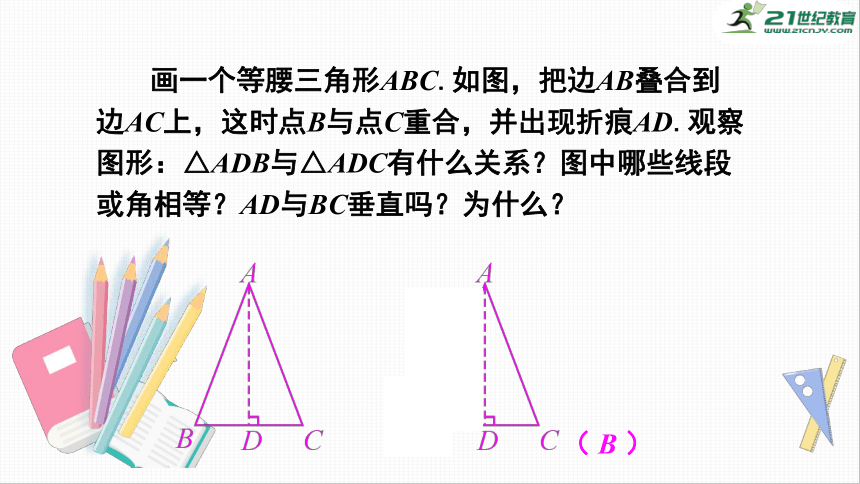
画一个等腰三角形ABC.如图,把边AB叠合到边AC上,这时点B与点C重合,并出现折痕AD.观察图形:△ADB与△ADC有什么关系?图中哪些线段或角相等?AD与BC垂直吗?为什么?
(
B
)
推进新课
定理1:等腰三角形两个底角相等,简称“等边对等角”.
定理2:等腰三角形顶角的平分线垂直平分底边.
等腰三角形顶角平分线、底边上的中线和底边上的高线三线合一.
推论:等边三角形三个内角相等,每一个内角都等于60°.
等腰三角形性质定理1的内容如何证明?
已知在△ABC中,AB=AC,求证:∠B=∠C.
证明:过A作AD⊥BC,垂足与于D,
∵AB=AC,AD=AD,∴Rt△ABD≌Rt△ACD(HL),
∴∠B=∠C.
例1
如图所示,在△ABC中,AB=AC,点D在AC上,且BD=BC=AD,求△ABC各角的度数.
【分析】首先应用等腰三角形的性质得到∠ABC=∠C=∠BDC,∠A=∠ABD,再运用三角形内角和定理求解得到∠A=36°,∠ABC=∠C=72°,这里可以运用代数的方法列式求解方程.
例2
如图所示,在△ABC中,AB=AC,∠BAC=120°,点D、E是底边上两点,且BD=AD,CE=AE,求∠DAE的度数.
解:∵AB=AC,
∴∠B=∠C.
∴∠B=∠C=
×(180°-120°)
=30°.
又∵BD=AD,
∴∠BAD=∠B=30°.
同理,∠CAE=∠C=30°
∴∠DAE=∠BAC-∠BAD-∠CAE
=120°-30°-30°=60°
巩固提升
1.如图,在下列等腰三角形中,分别求出它们的底角的度数.
解:图1中,∠B=∠C=
(180°-36°)=72°.
图2中,∠E=∠F=
(180°-120°)=30°.
2.如图,△ABC是等腰直角三角形,∠BAC=90°,AD是底边BC上的高,标∠B,∠C,∠BAD,∠DAC的度数,指出图中有哪些线段相等.
答:∠B=∠C=∠BAD=∠DAC=45°;
AB=AC,BD=DC=AD.
3.如图,在△ABC中,AB=AD=DC,∠BAD=26°,求∠B和∠C的度数.
解:AB=AD,∠BAD=26°,
∴∠B=∠ADB=
(180°-26°)=77°.
∴∠ADC=180°-77°=103°,
∴∠C=
(180°-103°)=38.5°
4.已知等腰三角形的腰长比底边多2cm,并且它的周长为16cm.求这个等腰三角形的边长.
解:设三角形的底边长为xcm,
则腰长为(x+2)cm,根据题意,
得x+2(x+2)=16,解得x=4.
∴等腰三角形的边长为4cm,6cm和6cm.
5.如图,在△ABC中,过C
作∠BAC的平分线AD的垂线,垂足为D,DE∥AB交AC于E.求证:AE=CE.
证明:延长CD交AB的延长线于P,
在△ADP和△ADC中,∠PAD=∠CAD,AD=AD,
∠PDA=∠CDA,∴△ADP?△ADC.
∴∠P=∠ACD.
又DE∥AP,∴∠CDE=∠P.∴∠CDE=ACD,
∴DE=EC.
同理可证,AE=DE,∴AE=CE.
6.已知:如图所示,△ABC是等腰直角三角形,∠A=90°,BD是∠ADE的平分线,DE⊥BC于E,若BC=10cm,求△DEC的周长.
解:∵△ABC为等腰三角形,且∠A=90°,
∴AB=AC,∠ABC=∠C=45°,
∵DE⊥BC,∴∠DEB=90°,
∵DB是∠ADE平分线,
∴∠BDA=∠BDE.
在△ADB与△EDB中,
∵
∴△BDA≌△BDE(AAS).
∴BA=BE,DA=DE.
∵△DEC的周长
=DE+DC+EC
=AD+DC+EC
=AC+EC=EB+EC=BC,
∴△DEC的周长为10cm.
(1)等腰三角形有哪些性质?
(2)你对本节课中等腰三角形与轴对称概念的联系有何体会?
课堂小结
1.从教材习题中选取完成练习;
2.完成练习册本课时的习题.
课后作业
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!
15.3
等腰三角形
第1课时
等腰三角形的性质
沪科版·八年级数学上册
上课课件
学习目标
【知识与技能】
进一步认识等腰三角形的定义和性质.
【过程与方法】
通过观察、操作、想象、推理和交流活动,理解等腰三角形“三线合一”等有关性质、提高几何推理意识.
【情感与态度】
通过对问题的发现和解决,培养学生合作精神,树立学好教学的信心,形成有条理的表达.
【教学重点】
重点是掌握等腰三角形的性质.
【教学难点】
难点是对等腰三角形“三线合一”的理解.
画一个等腰三角形ABC.如图,把边AB叠合到边AC上,这时点B与点C重合,并出现折痕AD.观察图形:△ADB与△ADC有什么关系?图中哪些线段或角相等?AD与BC垂直吗?为什么?
(
B
)
推进新课
定理1:等腰三角形两个底角相等,简称“等边对等角”.
定理2:等腰三角形顶角的平分线垂直平分底边.
等腰三角形顶角平分线、底边上的中线和底边上的高线三线合一.
推论:等边三角形三个内角相等,每一个内角都等于60°.
等腰三角形性质定理1的内容如何证明?
已知在△ABC中,AB=AC,求证:∠B=∠C.
证明:过A作AD⊥BC,垂足与于D,
∵AB=AC,AD=AD,∴Rt△ABD≌Rt△ACD(HL),
∴∠B=∠C.
例1
如图所示,在△ABC中,AB=AC,点D在AC上,且BD=BC=AD,求△ABC各角的度数.
【分析】首先应用等腰三角形的性质得到∠ABC=∠C=∠BDC,∠A=∠ABD,再运用三角形内角和定理求解得到∠A=36°,∠ABC=∠C=72°,这里可以运用代数的方法列式求解方程.
例2
如图所示,在△ABC中,AB=AC,∠BAC=120°,点D、E是底边上两点,且BD=AD,CE=AE,求∠DAE的度数.
解:∵AB=AC,
∴∠B=∠C.
∴∠B=∠C=
×(180°-120°)
=30°.
又∵BD=AD,
∴∠BAD=∠B=30°.
同理,∠CAE=∠C=30°
∴∠DAE=∠BAC-∠BAD-∠CAE
=120°-30°-30°=60°
巩固提升
1.如图,在下列等腰三角形中,分别求出它们的底角的度数.
解:图1中,∠B=∠C=
(180°-36°)=72°.
图2中,∠E=∠F=
(180°-120°)=30°.
2.如图,△ABC是等腰直角三角形,∠BAC=90°,AD是底边BC上的高,标∠B,∠C,∠BAD,∠DAC的度数,指出图中有哪些线段相等.
答:∠B=∠C=∠BAD=∠DAC=45°;
AB=AC,BD=DC=AD.
3.如图,在△ABC中,AB=AD=DC,∠BAD=26°,求∠B和∠C的度数.
解:AB=AD,∠BAD=26°,
∴∠B=∠ADB=
(180°-26°)=77°.
∴∠ADC=180°-77°=103°,
∴∠C=
(180°-103°)=38.5°
4.已知等腰三角形的腰长比底边多2cm,并且它的周长为16cm.求这个等腰三角形的边长.
解:设三角形的底边长为xcm,
则腰长为(x+2)cm,根据题意,
得x+2(x+2)=16,解得x=4.
∴等腰三角形的边长为4cm,6cm和6cm.
5.如图,在△ABC中,过C
作∠BAC的平分线AD的垂线,垂足为D,DE∥AB交AC于E.求证:AE=CE.
证明:延长CD交AB的延长线于P,
在△ADP和△ADC中,∠PAD=∠CAD,AD=AD,
∠PDA=∠CDA,∴△ADP?△ADC.
∴∠P=∠ACD.
又DE∥AP,∴∠CDE=∠P.∴∠CDE=ACD,
∴DE=EC.
同理可证,AE=DE,∴AE=CE.
6.已知:如图所示,△ABC是等腰直角三角形,∠A=90°,BD是∠ADE的平分线,DE⊥BC于E,若BC=10cm,求△DEC的周长.
解:∵△ABC为等腰三角形,且∠A=90°,
∴AB=AC,∠ABC=∠C=45°,
∵DE⊥BC,∴∠DEB=90°,
∵DB是∠ADE平分线,
∴∠BDA=∠BDE.
在△ADB与△EDB中,
∵
∴△BDA≌△BDE(AAS).
∴BA=BE,DA=DE.
∵△DEC的周长
=DE+DC+EC
=AD+DC+EC
=AC+EC=EB+EC=BC,
∴△DEC的周长为10cm.
(1)等腰三角形有哪些性质?
(2)你对本节课中等腰三角形与轴对称概念的联系有何体会?
课堂小结
1.从教材习题中选取完成练习;
2.完成练习册本课时的习题.
课后作业
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!
