15.3等腰三角形 第2课时 等腰三角形的判定 课件(共17张PPT)
文档属性
| 名称 | 15.3等腰三角形 第2课时 等腰三角形的判定 课件(共17张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-10 06:50:13 | ||
图片预览




文档简介
(共17张PPT)
第2课时
等腰三角形的判定
15.3
等腰三角形
沪科版·八年级数学上册
上课课件
学习目标
【知识与技能】
领会等腰三角形、等边三角形的判定方法,培养合情推理的能力.
【过程与方法】
通过探索等腰三角形、等边三角形判定方法的过程,学会对问题的解决,形成有条理的、清晰的表达能力.
【情感与态度】
通过对问题的发现和解决,培养学生空间思维,体会几何学的内涵和应用价值.
【教学重点】
重点是掌握等腰三角形、等边三角形的判定定理.
【教学难点】
难点是判定的应用,几何思维的形成.
新课导入
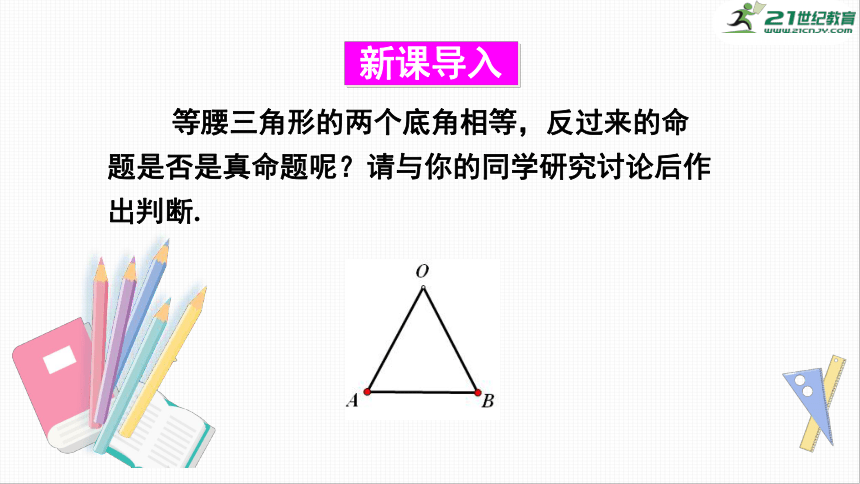
等腰三角形的两个底角相等,反过来的命题是否是真命题呢?请与你的同学研究讨论后作出判断.
定理有两个角相等的三角形是等腰三角形.(等角对等边)
新课讲解
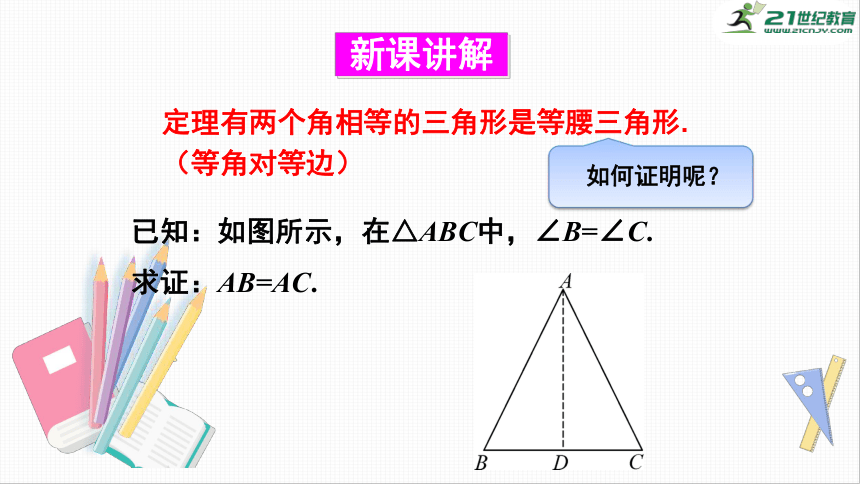
已知:如图所示,在△ABC中,∠B=∠C.
求证:AB=AC.
如何证明呢?
证明:过点A作AD⊥BC,D点为垂足,
∴∠ADB=∠ADC=90°.(垂直定义)
在△ADB和△ADC中,
∴△ADB≌△ADC.(AAS)
∴AB=AC(全等三角形的对应边相等)
由上述定理可得
推论1
三个角都相等的三角形是等边三角形.
推论2
有一个角是60°的等腰三角形是等边三角形.
定理
在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.
课堂演练
例1
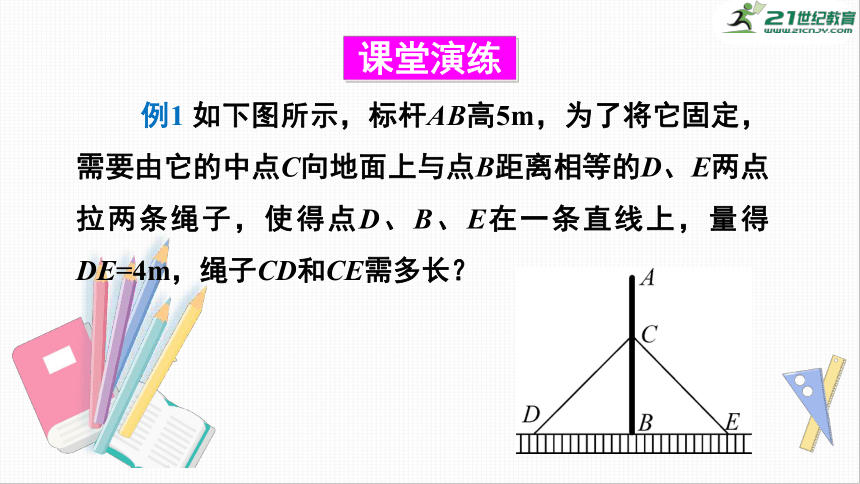
如下图所示,标杆AB高5m,为了将它固定,需要由它的中点C向地面上与点B距离相等的D、E两点拉两条绳子,使得点D、B、E在一条直线上,量得DE=4m,绳子CD和CE需多长?
解:∵AB=5m,C为AB中点,
∴AC=CB=2.5m
∵B为DE中点且DE=4
∴DB=BE=2m
∴CE=
m
在△CDB与△CEB中
∴△CDB≌△CEB(SAS)
∴CD=CE=
m
例2
如图,已知△ABC中,AB=AC,BD、CE分别是两腰上的中线.求证:BD=CE.
证明:AB=AC,∴∠ABC=∠ACB.
又CD=
AC,BE=
AB,
∴CD=BE.
在△BEC和△CDB中,
BE=CD,(已知)
∠ABC=∠ACB,(已证)
BC=CB,(公共边)
∴△BEC?△CDB(SAS).
∴BD=CE.
课后习题
1.如图,∠A=36°,∠DBC=36°,∠C=72°,分别计算∠1,∠2的度数,并说明图中有哪些等腰三角形.
答:∠1=72°,∠2=36°;
等腰三角形△ABC,△ABD,△BCD.
2.如图,AC和BD相交于点O,AB//DC,OA=OB.
求证:OC=OD.
证明:OA=OB,∴∠A=∠B,
又AB//DC,
∴∠A=∠C,∠B=∠D,
∴∠C=∠D,
∴OC=OD.
3.如图,在△ABD中,C是BD上的一点,且AC⊥BD,AC=BC=CD.求证:
(1)△ABD是等腰三角形.
(2)求∠BAD的度数.
(1)证明:∵AC⊥BD,
∴∠ACB=∠ACD=90°,
又AC=BC=CD,
∴△ABC?△ADC(SAS),
∴AB=AD,即△ABD是等腰三角形.
(2)由(1)可知,AB=AD,
∴∠B=∠D,又AC=BC=CD,
∴∠B=∠BAC,∠D=∠DAC.
在△ABD中,∠B+∠BAC+∠DAC+∠D=180°,
∴2(∠BAC+∠DAC)=180°,
∴∠BAC+∠DAC=90°,
∴∠BAD=∠BAC+∠DAC=90°.
1.本节课学习了哪些内容?这些内容在应用方面你有什么看法?
2.你能将等腰三角形的知识体系简单地说一说吗?
3.本节课中,你与同伴交流,学到了同伴的哪些优点?
课堂小结
1.从教材习题中选取完成练习;
2.完成练习册本课时的习题.
课后作业
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!
第2课时
等腰三角形的判定
15.3
等腰三角形
沪科版·八年级数学上册
上课课件
学习目标
【知识与技能】
领会等腰三角形、等边三角形的判定方法,培养合情推理的能力.
【过程与方法】
通过探索等腰三角形、等边三角形判定方法的过程,学会对问题的解决,形成有条理的、清晰的表达能力.
【情感与态度】
通过对问题的发现和解决,培养学生空间思维,体会几何学的内涵和应用价值.
【教学重点】
重点是掌握等腰三角形、等边三角形的判定定理.
【教学难点】
难点是判定的应用,几何思维的形成.
新课导入
等腰三角形的两个底角相等,反过来的命题是否是真命题呢?请与你的同学研究讨论后作出判断.
定理有两个角相等的三角形是等腰三角形.(等角对等边)
新课讲解
已知:如图所示,在△ABC中,∠B=∠C.
求证:AB=AC.
如何证明呢?
证明:过点A作AD⊥BC,D点为垂足,
∴∠ADB=∠ADC=90°.(垂直定义)
在△ADB和△ADC中,
∴△ADB≌△ADC.(AAS)
∴AB=AC(全等三角形的对应边相等)
由上述定理可得
推论1
三个角都相等的三角形是等边三角形.
推论2
有一个角是60°的等腰三角形是等边三角形.
定理
在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.
课堂演练
例1
如下图所示,标杆AB高5m,为了将它固定,需要由它的中点C向地面上与点B距离相等的D、E两点拉两条绳子,使得点D、B、E在一条直线上,量得DE=4m,绳子CD和CE需多长?
解:∵AB=5m,C为AB中点,
∴AC=CB=2.5m
∵B为DE中点且DE=4
∴DB=BE=2m
∴CE=
m
在△CDB与△CEB中
∴△CDB≌△CEB(SAS)
∴CD=CE=
m
例2
如图,已知△ABC中,AB=AC,BD、CE分别是两腰上的中线.求证:BD=CE.
证明:AB=AC,∴∠ABC=∠ACB.
又CD=
AC,BE=
AB,
∴CD=BE.
在△BEC和△CDB中,
BE=CD,(已知)
∠ABC=∠ACB,(已证)
BC=CB,(公共边)
∴△BEC?△CDB(SAS).
∴BD=CE.
课后习题
1.如图,∠A=36°,∠DBC=36°,∠C=72°,分别计算∠1,∠2的度数,并说明图中有哪些等腰三角形.
答:∠1=72°,∠2=36°;
等腰三角形△ABC,△ABD,△BCD.
2.如图,AC和BD相交于点O,AB//DC,OA=OB.
求证:OC=OD.
证明:OA=OB,∴∠A=∠B,
又AB//DC,
∴∠A=∠C,∠B=∠D,
∴∠C=∠D,
∴OC=OD.
3.如图,在△ABD中,C是BD上的一点,且AC⊥BD,AC=BC=CD.求证:
(1)△ABD是等腰三角形.
(2)求∠BAD的度数.
(1)证明:∵AC⊥BD,
∴∠ACB=∠ACD=90°,
又AC=BC=CD,
∴△ABC?△ADC(SAS),
∴AB=AD,即△ABD是等腰三角形.
(2)由(1)可知,AB=AD,
∴∠B=∠D,又AC=BC=CD,
∴∠B=∠BAC,∠D=∠DAC.
在△ABD中,∠B+∠BAC+∠DAC+∠D=180°,
∴2(∠BAC+∠DAC)=180°,
∴∠BAC+∠DAC=90°,
∴∠BAD=∠BAC+∠DAC=90°.
1.本节课学习了哪些内容?这些内容在应用方面你有什么看法?
2.你能将等腰三角形的知识体系简单地说一说吗?
3.本节课中,你与同伴交流,学到了同伴的哪些优点?
课堂小结
1.从教材习题中选取完成练习;
2.完成练习册本课时的习题.
课后作业
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!
