13.2命题与证明 第2课时 证明 课件(共30张PPT)
文档属性
| 名称 | 13.2命题与证明 第2课时 证明 课件(共30张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-10 00:00:00 | ||
图片预览








文档简介
(共21张PPT)
第2课时
证明
沪科版·八年级数学上册
上课课件
13.2
命题与证明
学习目标
【知识与技能】
了解公理、定理、证明的内涵,会进行简单的推理.
【过程与方法】
经历探索证明的过程,弄清证明的基本方法以及书写格式,体会演绎推理的意义.
【情感与态度】
培养严谨的推理能力和表述能力,感受证明的几何价值.
【教学重点】
重点是掌握推理方法.
【教学难点】
难点是培养演绎推理意识.
新课导入
在日常生活、实践中,大家常常把公认的并且长期检验所取得的真命题作为论证其它命题的根据,这样的最原始的真命题我们称之为公理.
思
考
你能举出几个前面已学过的公理吗?
(1)两点确定一条直线.
(2)经过直线外一点,有且只有一条直线平行于已知直线.
(3)两点之间,线段最短
.
有些命题,如:“对顶角相等”,“三角形三个内角的和等于180°”等,它们的正确性已经经过推理得到证实,并被作为判断其他命题真假的依据,这样的真命题称为定理。
从已知条件出发,根据定义、基本事实、已证定理,并按照逻辑规则,推导出结论的方法叫“演绎推理”。推理的过程叫做证明.
回顾我们学过的命题,哪些是定理?
平行线判定定理:内错角相等,两直线平行.
同旁内角互补,两直线平行.
平行线性质定理:两直线平行,内错角相等.
两直线平行,同旁内角互补.
三角形内角和定理:三角形内角和等于180度.
思
考
证
明
证明的步骤:(1)________________;
(2)________________
(3)________________
根据题意画出图形
根据题设、结论,结合图形,写出已知、求证;
经过分析,找出已知条件推出结论的途径,写出证明过程;
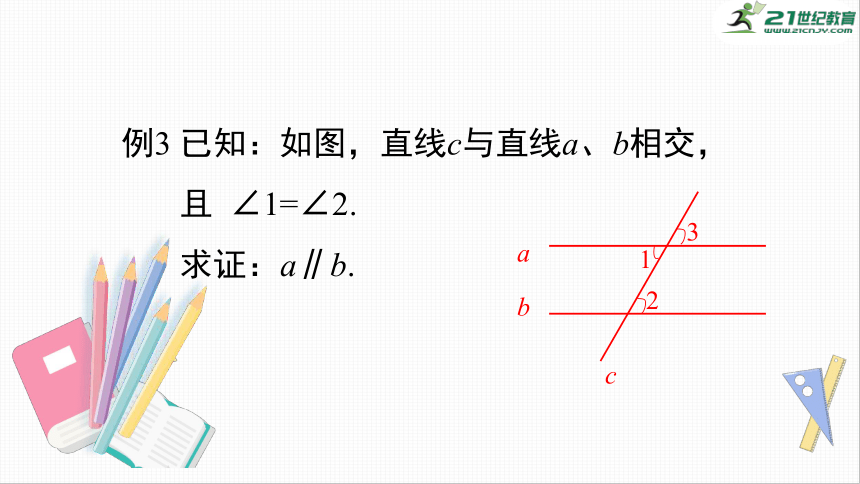
例3
已知:如图,直线c与直线a、b相交,
且
∠1=∠2.
求证:a∥b.
a
b
c
3
1
2
证明:
∵
∠1=∠2,
(
)
又∵
∠1=∠3,(
)
∴∠2=∠3,
(
)
∴
a∥b,
(
)
已知
对顶角相等
等量代换
同位角相等,两直线平行
练
习
在下列各题的括号内,填上推理的依据:
1.已知:如图,点B、A、E在一条直线上,∠1=∠B.
求证:∠2=∠C.
A
B
C
D
E
1
2
A
B
C
D
E
1
2
证明
∵∠1=∠B(
)
∴AD∥BC(
)
∴∠2=∠C(
)
已知
同位角相等,两直线平行
两直线平行,内错角相等
2.
已知,如图,∠1=∠2.
求证:AB∥CD
A
B
C
D
E
F
1
2
3
A
B
C
D
E
F
1
2
3
证明
∵∠1=∠2(
)
又∵∠2∥∠3(
)
∴∠1=∠3(
)
∴AB//CD(
)
已知
对顶角相等
等量代换
同位角相等,两直线平行
例4
已知:如图,∠AOB+∠BOC=180°,OE
平分∠AOB,OF平分∠BOC.
求证:OE⊥OF.
A
O
C
B
E
F
1
2
证明
∵OE平分∠AOB,OF平分∠BOC,(已知)
∴∠1=
∠AOB,∠2=
∠BOC.(角平分线定义)
又∵∠AOB+∠BOC=180°,(已知)
∴∠1+∠2=
(∠AOB+∠BOC)
=90°.(等式性质)
∴OE⊥OF.(垂直的定义)
A
O
C
B
E
F
1
2
A
B
C
D
E
F
1
2
已知:如图,DC//AB,DF平分∠CDB,BE平分∠ABD.
求证:∠1
=
∠2.
练
习
证明
∵DC//AB(
)
∴∠ABD=∠CDB.(
)
又
∵DF平分∠CDB,(
)
BE平分∠ABD,(
)
∴∠1=
∠
,(
)
∠2=
∠
.(
)
∴∠1=∠2.(
)
已知
两直线平行,内错角相等
已知
已知
CDB
角平分线的定义
ABD
角平分线的定义
等量代换
A
B
C
D
E
F
1
2
1.从教材习题中选取,
2.完成练习册本课时的习题.
课后作业
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!
第2课时
证明
沪科版·八年级数学上册
上课课件
13.2
命题与证明
学习目标
【知识与技能】
了解公理、定理、证明的内涵,会进行简单的推理.
【过程与方法】
经历探索证明的过程,弄清证明的基本方法以及书写格式,体会演绎推理的意义.
【情感与态度】
培养严谨的推理能力和表述能力,感受证明的几何价值.
【教学重点】
重点是掌握推理方法.
【教学难点】
难点是培养演绎推理意识.
新课导入
在日常生活、实践中,大家常常把公认的并且长期检验所取得的真命题作为论证其它命题的根据,这样的最原始的真命题我们称之为公理.
思
考
你能举出几个前面已学过的公理吗?
(1)两点确定一条直线.
(2)经过直线外一点,有且只有一条直线平行于已知直线.
(3)两点之间,线段最短
.
有些命题,如:“对顶角相等”,“三角形三个内角的和等于180°”等,它们的正确性已经经过推理得到证实,并被作为判断其他命题真假的依据,这样的真命题称为定理。
从已知条件出发,根据定义、基本事实、已证定理,并按照逻辑规则,推导出结论的方法叫“演绎推理”。推理的过程叫做证明.
回顾我们学过的命题,哪些是定理?
平行线判定定理:内错角相等,两直线平行.
同旁内角互补,两直线平行.
平行线性质定理:两直线平行,内错角相等.
两直线平行,同旁内角互补.
三角形内角和定理:三角形内角和等于180度.
思
考
证
明
证明的步骤:(1)________________;
(2)________________
(3)________________
根据题意画出图形
根据题设、结论,结合图形,写出已知、求证;
经过分析,找出已知条件推出结论的途径,写出证明过程;
例3
已知:如图,直线c与直线a、b相交,
且
∠1=∠2.
求证:a∥b.
a
b
c
3
1
2
证明:
∵
∠1=∠2,
(
)
又∵
∠1=∠3,(
)
∴∠2=∠3,
(
)
∴
a∥b,
(
)
已知
对顶角相等
等量代换
同位角相等,两直线平行
练
习
在下列各题的括号内,填上推理的依据:
1.已知:如图,点B、A、E在一条直线上,∠1=∠B.
求证:∠2=∠C.
A
B
C
D
E
1
2
A
B
C
D
E
1
2
证明
∵∠1=∠B(
)
∴AD∥BC(
)
∴∠2=∠C(
)
已知
同位角相等,两直线平行
两直线平行,内错角相等
2.
已知,如图,∠1=∠2.
求证:AB∥CD
A
B
C
D
E
F
1
2
3
A
B
C
D
E
F
1
2
3
证明
∵∠1=∠2(
)
又∵∠2∥∠3(
)
∴∠1=∠3(
)
∴AB//CD(
)
已知
对顶角相等
等量代换
同位角相等,两直线平行
例4
已知:如图,∠AOB+∠BOC=180°,OE
平分∠AOB,OF平分∠BOC.
求证:OE⊥OF.
A
O
C
B
E
F
1
2
证明
∵OE平分∠AOB,OF平分∠BOC,(已知)
∴∠1=
∠AOB,∠2=
∠BOC.(角平分线定义)
又∵∠AOB+∠BOC=180°,(已知)
∴∠1+∠2=
(∠AOB+∠BOC)
=90°.(等式性质)
∴OE⊥OF.(垂直的定义)
A
O
C
B
E
F
1
2
A
B
C
D
E
F
1
2
已知:如图,DC//AB,DF平分∠CDB,BE平分∠ABD.
求证:∠1
=
∠2.
练
习
证明
∵DC//AB(
)
∴∠ABD=∠CDB.(
)
又
∵DF平分∠CDB,(
)
BE平分∠ABD,(
)
∴∠1=
∠
,(
)
∠2=
∠
.(
)
∴∠1=∠2.(
)
已知
两直线平行,内错角相等
已知
已知
CDB
角平分线的定义
ABD
角平分线的定义
等量代换
A
B
C
D
E
F
1
2
1.从教材习题中选取,
2.完成练习册本课时的习题.
课后作业
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!
