第13章 三角形中的边角关系、命题与证明 本章复习 课件(共30张PPT)
文档属性
| 名称 | 第13章 三角形中的边角关系、命题与证明 本章复习 课件(共30张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-10 07:30:01 | ||
图片预览








文档简介
(共30张PPT)
本章复习
沪科版·八年级数学上册
上课课件
第13章
三角形中的边角关系、命题与证明
学习目标
【知识与技能】
1.理解并掌握三角形及三角形的重要线段的概念;
2.掌握三角形的三边间的关系;
3.会利用三角形的内角和定理及外角公式计算角度.
4.掌握证明命题的一般步骤.
【过程与方法】
理解并掌握三角形及三角形的重要线段的概念;掌握三角形的三边间的关系;会利用三角形的内角和定理及外角公式计算角度.
掌握证明命题的一般步骤,经历知识的形成过程,增强学生的逻辑思维能力.
【情感与态度】
培养合作交流、探索求实的思想.
【教学重点】
重点是会灵活运用内角和定理及外角公式计算角度.
【教学难点】
难点是证明命题推理分析的过程.
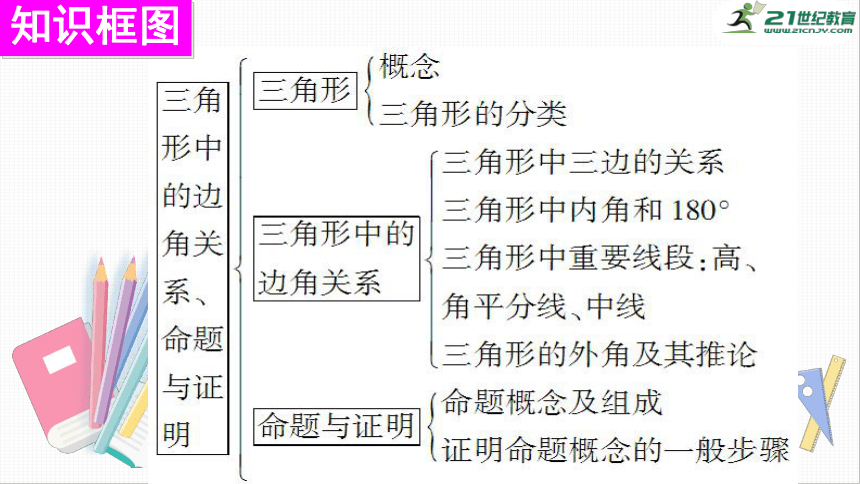
知识框图
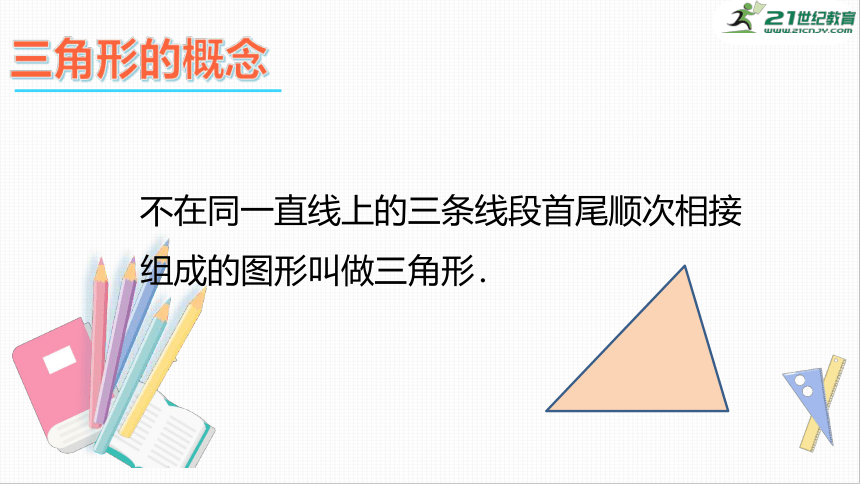
三角形的概念
不在同一直线上的三条线段首尾顺次相接组成的图形叫做三角形.
①三角形有三条边,三个内角,三个顶点.
②组成三角形的线段叫做三角形的边;
③相邻两边所组成的角叫做三角形内角,简称角;
④相邻两边的公共端点是三角形的顶点,
三角形ABC用符号表示为△ABC;
⑤三角形ABC的边AB可用边AB所对的角C的小写字母c
表示,AC可用b表示,BC可用a表示.
三角形的三边关系
三角形的任意两边之和大于第三边;
三角形的任意两边之差小于第三边.
判断三条线段能否构成三角形的方法:只要满足较小的两条线段之和大于第三条线段,便可构成三角形;若不满足,则不能构成三角形.
三角形的高、中线、角平分线
(1)三角形的高:从三角形的一个顶点向它的对边所在的直线作垂线,顶点和垂足之间的线段
注意:
①
三角形的高是线段;
②
锐角三角形三条高全在三角形的内部;
直角三角形有两条高是直角边,另一条在内部;
钝角三角形有两条高在三角形外,另一条在内部。
③
三角形三条高所在直线交于一点.
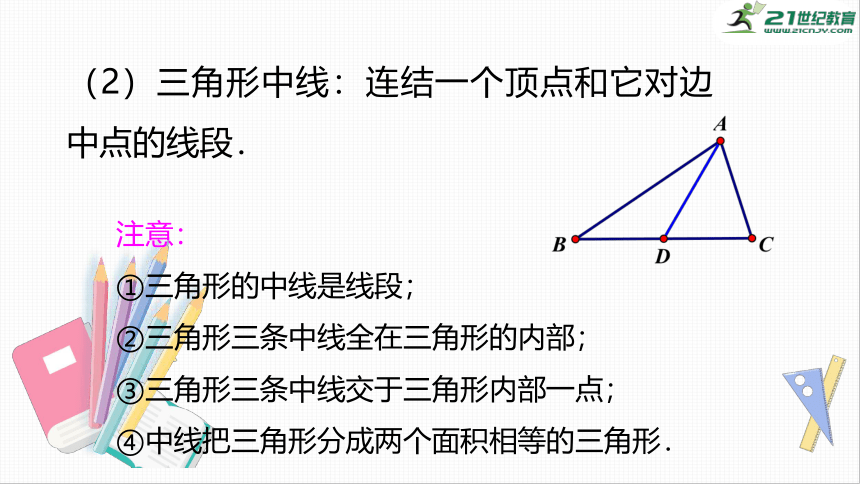
(2)三角形中线:连结一个顶点和它对边中点的线段.
注意:
①三角形的中线是线段;
②三角形三条中线全在三角形的内部;
③三角形三条中线交于三角形内部一点;
④中线把三角形分成两个面积相等的三角形.
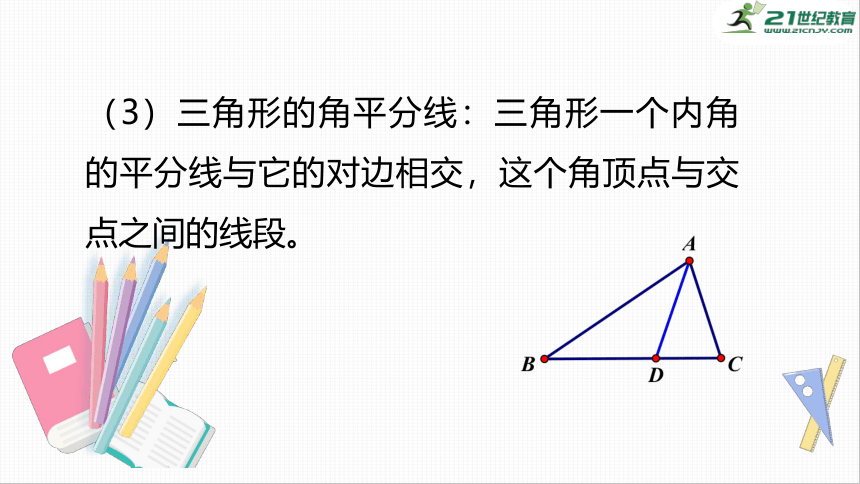
(3)三角形的角平分线:三角形一个内角的平分线与它的对边相交,这个角顶点与交点之间的线段。
注意:
①三角形的角平分线是线段;
②三角形三条角平分线全在三角形的内部;
③三角形三条角平分线交于三角形内部一点;
④用量角器画三角形的角平分线.
有关“命题”的概念
对某一事件作出正确或不正确判断的语句叫做命题。
注意:
①
命题有真命题和假命题两种,
②
命题由题设和结论两部分组成的.
前一部分,也称之为条件,后一部分称之为结论。
③
命题通常是用“如果……,
那么…….”的形式给出.
④
“如果p,那么q.”中的题设与结论互换,得一个新命题:
“如果q,那么p.”这两个命题称为互逆命题.其中一个命题叫原命题,另一个命题叫做逆命题.
⑤
当一个命题是真命题时它的逆命题不一定是真命题.
⑥
符合命题的题设,但不满足命题的结论的例子,称之为反例.
要说明一个命题是假命题,只要举一个反例即可.
有关“公理、定理、证明、推论、演绎推理、辅助线”等概念
(1)公理:从长期实践中总结出来的,不需要再作证明的真命题.
(2)定理:从公理或其他真命题出发,用推理方法证明为正确的,并被选作判断命题真假的依据的真命题.
(3)推论:由公理、定理直接得出的真命题。
(4)演绎推理:从已知条件出发,依据定义、公理、定理,并按照逻辑规则,推导出结论的方法。
(5)证明:演绎推理的过程就是演绎证明,简称“证明”.
(6)辅助线:为了证明的需要,在原来的图形上添画的线段或直线.
三角形的内角和等于180°.
三角形的内角和定理
三角形一边与另一边的延长线组成的角,叫做三角形的外角.
三角形的外角
1.三角形的一个外角与它相邻的内角互补;
2.三角形的一个外角等于它不相邻的两个内角的和;
3.三角形的一个外角大于任何一个与它不相邻的内角.
4.三角形的外角和为360°.
三角形的外角与内角的关系:
考点一:数三角形的个数
例1
图中三角形的个数是(
)
A.8
B.9
C.10
D.11
B
考点二:三角形三边关系
例2
已知四组线段的长分别如下,以各组线段为边,能组成三角形的是(
)
A.1,2,3
B.2,5,8
C.3,4,5
D.4,5,10
C
例3
下列各组条件中,不能组成三角形的是(
)
A.
a+1、a+2、a+3
(a>3)
B.
3cm、8cm、10
cm
C.
三条线段之比为1:2:3
D.
3a、5a、2a+1
(a>1)
C
考点三:三角形的三线
例4
下列说法错误的是(
)
A、三角形的三条中线都在三角形内。
B、直角三角形的高线只有一条。
C、三角形的三条角平分线都在三角形内。
D、钝角三角形内只有一条高线。
B
例5
在三条边都不相等的三角形中,同一条
边上的中线,高和这边所对角的角平分线,最短的是(
)
A.
中线.
B.
高线.
C.
角平分线.
D.
不能确定.
B
考点四
三角形内角和定理:
例6
△ABC中,∠B=
∠A=
∠C,求
△ABC的三个内角度数.
解:设∠B=x?
,则∠A=3x?,∠C=4x?
,
从而:x+3x+4x=180?,解得x=22.5?.
即:∠B=22.5?,∠A=67.5?,∠C=90?.
例7
如图,点O是△ABC内一点,∠A=80°,∠1=15°,∠2=40°,则∠BOC等于(
)
A.
95°
B.
120°
C.
135°
D.
65°
C
1.从教材习题中选取,
2.完成练习册本课时的习题.
课后作业
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!
本章复习
沪科版·八年级数学上册
上课课件
第13章
三角形中的边角关系、命题与证明
学习目标
【知识与技能】
1.理解并掌握三角形及三角形的重要线段的概念;
2.掌握三角形的三边间的关系;
3.会利用三角形的内角和定理及外角公式计算角度.
4.掌握证明命题的一般步骤.
【过程与方法】
理解并掌握三角形及三角形的重要线段的概念;掌握三角形的三边间的关系;会利用三角形的内角和定理及外角公式计算角度.
掌握证明命题的一般步骤,经历知识的形成过程,增强学生的逻辑思维能力.
【情感与态度】
培养合作交流、探索求实的思想.
【教学重点】
重点是会灵活运用内角和定理及外角公式计算角度.
【教学难点】
难点是证明命题推理分析的过程.
知识框图
三角形的概念
不在同一直线上的三条线段首尾顺次相接组成的图形叫做三角形.
①三角形有三条边,三个内角,三个顶点.
②组成三角形的线段叫做三角形的边;
③相邻两边所组成的角叫做三角形内角,简称角;
④相邻两边的公共端点是三角形的顶点,
三角形ABC用符号表示为△ABC;
⑤三角形ABC的边AB可用边AB所对的角C的小写字母c
表示,AC可用b表示,BC可用a表示.
三角形的三边关系
三角形的任意两边之和大于第三边;
三角形的任意两边之差小于第三边.
判断三条线段能否构成三角形的方法:只要满足较小的两条线段之和大于第三条线段,便可构成三角形;若不满足,则不能构成三角形.
三角形的高、中线、角平分线
(1)三角形的高:从三角形的一个顶点向它的对边所在的直线作垂线,顶点和垂足之间的线段
注意:
①
三角形的高是线段;
②
锐角三角形三条高全在三角形的内部;
直角三角形有两条高是直角边,另一条在内部;
钝角三角形有两条高在三角形外,另一条在内部。
③
三角形三条高所在直线交于一点.
(2)三角形中线:连结一个顶点和它对边中点的线段.
注意:
①三角形的中线是线段;
②三角形三条中线全在三角形的内部;
③三角形三条中线交于三角形内部一点;
④中线把三角形分成两个面积相等的三角形.
(3)三角形的角平分线:三角形一个内角的平分线与它的对边相交,这个角顶点与交点之间的线段。
注意:
①三角形的角平分线是线段;
②三角形三条角平分线全在三角形的内部;
③三角形三条角平分线交于三角形内部一点;
④用量角器画三角形的角平分线.
有关“命题”的概念
对某一事件作出正确或不正确判断的语句叫做命题。
注意:
①
命题有真命题和假命题两种,
②
命题由题设和结论两部分组成的.
前一部分,也称之为条件,后一部分称之为结论。
③
命题通常是用“如果……,
那么…….”的形式给出.
④
“如果p,那么q.”中的题设与结论互换,得一个新命题:
“如果q,那么p.”这两个命题称为互逆命题.其中一个命题叫原命题,另一个命题叫做逆命题.
⑤
当一个命题是真命题时它的逆命题不一定是真命题.
⑥
符合命题的题设,但不满足命题的结论的例子,称之为反例.
要说明一个命题是假命题,只要举一个反例即可.
有关“公理、定理、证明、推论、演绎推理、辅助线”等概念
(1)公理:从长期实践中总结出来的,不需要再作证明的真命题.
(2)定理:从公理或其他真命题出发,用推理方法证明为正确的,并被选作判断命题真假的依据的真命题.
(3)推论:由公理、定理直接得出的真命题。
(4)演绎推理:从已知条件出发,依据定义、公理、定理,并按照逻辑规则,推导出结论的方法。
(5)证明:演绎推理的过程就是演绎证明,简称“证明”.
(6)辅助线:为了证明的需要,在原来的图形上添画的线段或直线.
三角形的内角和等于180°.
三角形的内角和定理
三角形一边与另一边的延长线组成的角,叫做三角形的外角.
三角形的外角
1.三角形的一个外角与它相邻的内角互补;
2.三角形的一个外角等于它不相邻的两个内角的和;
3.三角形的一个外角大于任何一个与它不相邻的内角.
4.三角形的外角和为360°.
三角形的外角与内角的关系:
考点一:数三角形的个数
例1
图中三角形的个数是(
)
A.8
B.9
C.10
D.11
B
考点二:三角形三边关系
例2
已知四组线段的长分别如下,以各组线段为边,能组成三角形的是(
)
A.1,2,3
B.2,5,8
C.3,4,5
D.4,5,10
C
例3
下列各组条件中,不能组成三角形的是(
)
A.
a+1、a+2、a+3
(a>3)
B.
3cm、8cm、10
cm
C.
三条线段之比为1:2:3
D.
3a、5a、2a+1
(a>1)
C
考点三:三角形的三线
例4
下列说法错误的是(
)
A、三角形的三条中线都在三角形内。
B、直角三角形的高线只有一条。
C、三角形的三条角平分线都在三角形内。
D、钝角三角形内只有一条高线。
B
例5
在三条边都不相等的三角形中,同一条
边上的中线,高和这边所对角的角平分线,最短的是(
)
A.
中线.
B.
高线.
C.
角平分线.
D.
不能确定.
B
考点四
三角形内角和定理:
例6
△ABC中,∠B=
∠A=
∠C,求
△ABC的三个内角度数.
解:设∠B=x?
,则∠A=3x?,∠C=4x?
,
从而:x+3x+4x=180?,解得x=22.5?.
即:∠B=22.5?,∠A=67.5?,∠C=90?.
例7
如图,点O是△ABC内一点,∠A=80°,∠1=15°,∠2=40°,则∠BOC等于(
)
A.
95°
B.
120°
C.
135°
D.
65°
C
1.从教材习题中选取,
2.完成练习册本课时的习题.
课后作业
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!
