北师大版八年级数学上册《4.1 函数》同步练习(Word版 含答案)
文档属性
| 名称 | 北师大版八年级数学上册《4.1 函数》同步练习(Word版 含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 89.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-09 15:13:13 | ||
图片预览


文档简介
4.1 函数
一.选择题
1.下列图象中,y不是x的函数的是( )
A. B.
C. D.
2.下列式子中,y不是x的函数的是( )
A.y=x2 B.y= C.y= D.y=±
3.在行进路程s、速度v和时间t的相关计算中,若保持行驶的路程不变,则下列说法正确的是( )
A.速度v是变量
B.时间t是变量
C.速度v和时间t都是变量
D.速度v、时间t、路程s都是常量
4.已知声音在空气中的传播速度与空气的温度有关,在一定范围内,其关系如表所示,下列说法错误的是( )
温度/℃ ﹣20 ﹣10 0 10 20 30
传播速度/m/s 318 324 330 336 342 348
A.自变量是温度,因变量是传播速度
B.温度越高,传播速度越快
C.当温度为10℃时,声音5s可以传播1650m
D.温度每升高10℃,传播速度增加6m/s
5.函数y=中自变量x的取值范围是( )
A.x≠0 B.x≥2或x≠0 C.x≥2 D.x≤﹣2且x≠0
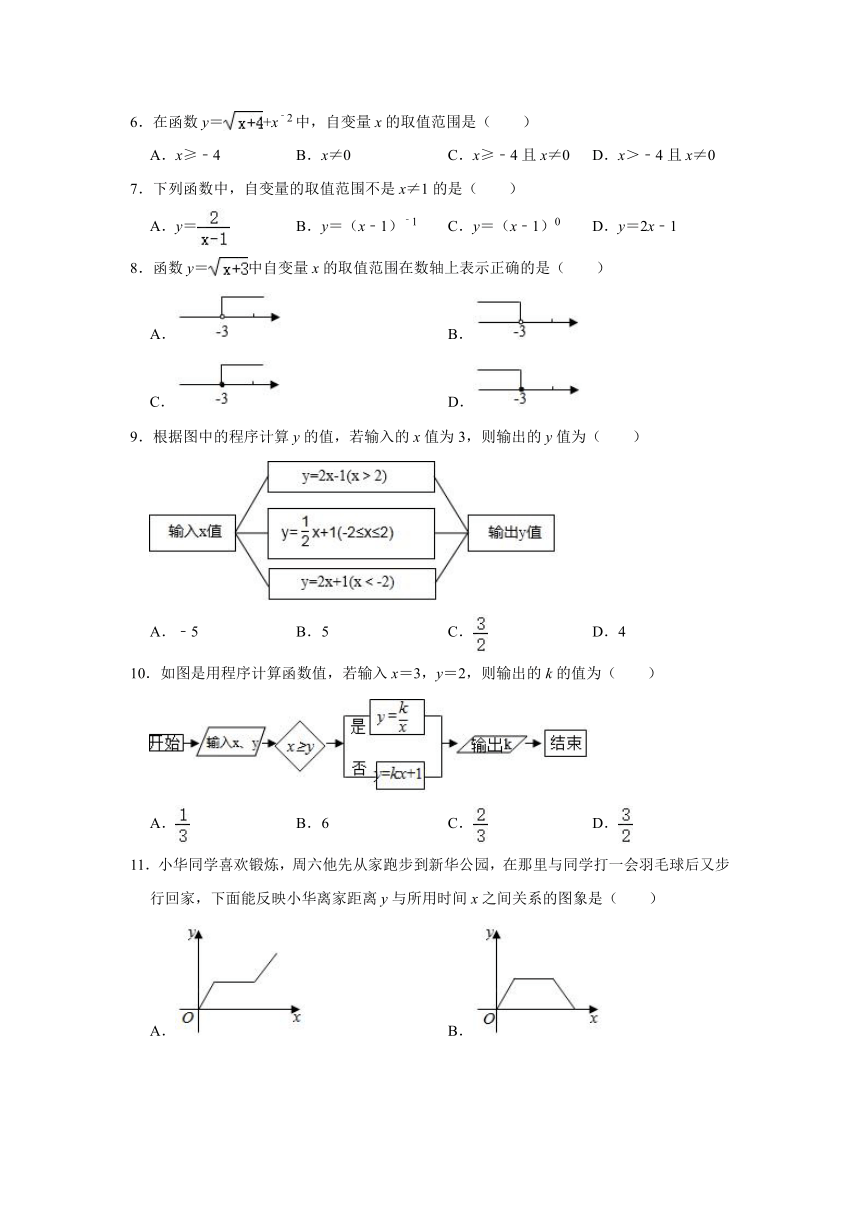
6.在函数y=+x﹣2中,自变量x的取值范围是( )
A.x≥﹣4 B.x≠0 C.x≥﹣4且x≠0 D.x>﹣4且x≠0
7.下列函数中,自变量的取值范围不是x≠1的是( )
A.y= B.y=(x﹣1)﹣1 C.y=(x﹣1)0 D.y=2x﹣1
8.函数y=中自变量x的取值范围在数轴上表示正确的是( )
A. B.
C. D.
9.根据图中的程序计算y的值,若输入的x值为3,则输出的y值为( )
A.﹣5 B.5 C. D.4
10.如图是用程序计算函数值,若输入x=3,y=2,则输出的k的值为( )
A. B.6 C. D.
11.小华同学喜欢锻炼,周六他先从家跑步到新华公园,在那里与同学打一会羽毛球后又步行回家,下面能反映小华离家距离y与所用时间x之间关系的图象是( )
A. B.
C. D.
12.某地区用电量与应缴电费之间的关系如下表:则下列叙述错误的是( )
用电量(千瓦?时) 1 2 3 4 …
应缴电费(元) 0.55 1.10 1.65 2.20 …
A.用电量每增加1千瓦?时,电费增加0.55元
B.若用电量为8千瓦?时,则应缴电费4.4元
C.若应缴电费为2.75元,则用电量为6千瓦?时
D.应缴电费随用电量的增加而增加
二.填空题
13.已知y=kx+b,其中y,k,x均不等于零,用y,b,x表示k,则k= .
14.下列:①y=x2;②y=2x+1;③y2=2x(x≥0);④y=(x≥0),具有函数关系(自变量为x)的是 .
15.小亮拿15元钱去文具店买签字笔,每支1.5元,小亮买签字笔后所剩钱数y(元)与买签字笔的支数x(支)之间的关系式为 .
16.函数y=中,自变量的取值范围是 .
17.下表中y与x的数据满足我们初中学过的某种函数关系.其函数表达式为 .
x … ﹣1 0 1 3 …
y … 0 3 4 0 …
三.解答题
18.在一次实验中,小强把一根弹簧的上端固定,在其下端悬挂物体.下面是他测得的弹簧的长度y与所挂物体的质量x的一组对应值:
所挂物体的质量x/kg 0 1 2 3 4 5
弹簧的长度y/cm 20 22 24 26 28 30
(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)填空:
①当所挂的物体为3kg时,弹簧长是 .不挂重物时,弹簧长是 .
②当所挂物体的质量为8kg(在弹簧的弹性限度范围内)时,弹簧长度是 .
19.如图所示,在△ABC中,底边BC=8cm,高AD=6cm,E为AD上一动点,当点E从点D向点A运动时,△BEC的面积发生了变化.
(1)在这个变化过程中,自变量和因变量各是什么?
(2)若设DE长为x(cm),△BEC的面积为y,求y与x之间的关系式.
(3)当DE长度为3cm时,△BEC的面积y是多少?
20.求下列函数中自变量x的取值范围.
(1)y=3x﹣1;
(2)y=+;
(3)y=.
21.已知y=(a﹣1)x+2a﹣4,当x=﹣1时,y=0.
(1)求a的值;
(2)当x=1时,求y的值.
22.某公交车每月的支出费用为4000元,每月的乘车人数x(人)与每月利润(利润=收入费用﹣支出费用)y(元)的变化关系如下表所示(每位乘客的公交票价是固定不变的):
x(人) 500 1000 1500 2000 2500 3000 …
y(元) ﹣3000 ﹣2000 ﹣1000 0 1000 2000 …
(1)在这个变化过程中, 是自变量, 是因变量;
(2)观察表中数据可知,每月乘客量达到 人以上时,该公交车才不会亏损;
(3)请你估计当每月乘车人数为3500人时,每月利润为多少元?
(4)若5月份想获得利润5000元,则请你估计5月份的乘客量需达 人.
参考答案
一.选择题
1. C.
2. D.
3. C.
4. C.
5. C.
6. C.
7. D.
8. C.
9. B.
10. B.
11. B.
12. C.
二.填空题
13. .
14.①②.
15. y=15﹣1.5x.
16. x≥1且x≠3.
17. y=﹣x2+2x+3.
三.解答题
18.(1)反映了弹簧长度y与所挂物体质量x之间的关系,所挂物体的质量是自变量,弹簧的长度是因变量;
(2)①根据表格可知:当所挂物体重量为3千克时,弹簧长度为26cm;不挂重物时,弹簧长度为10cm;
故答案为:26cm 20cm.
②根据表格可知:所挂重物每增加1千克,弹簧增长2cm,根据弹簧的长度=弹簧原来的长度+弹簧伸长的长度可知当所挂物体的重量为x千克时,弹簧长度y=2x+20,将x=8代入得y=2×8+20=36.
故答案为:36cm.
19.(1)在这个变化过程中,自变量为DE的长,因变量是△BEC的面积;
(2)y=×BC×DE=4x(0≤x≤6);
(3)当x=3时,y=4×3=12(cm2).
20.(1)x是任意实数;
(2)根据题意得:,
解得:x≥2且x≠3;
(3)根据题意得:x﹣1≠0,
解得:x≠1.
21.(1)由y=(a﹣1)x+2a﹣4,当x=﹣1时,y=0,得
﹣(a﹣1)+2a﹣4=0,
解得a=3;
(2)函数解析式为y=2x+2,
当x=1时,y=2+2=4.
22.(1)在这个变化过程中,每月的乘车人数x是自变量,每月的利润y是因变量;
故答案为每月的乘车人数x,每月的利润y;
(2)观察表中数据可知,每月乘客量达到观察表中数据可知,每月乘客量达到2000人以上时,该公交车才不会亏损;
故答案为2000;
(3)由表中数据可知,每月的乘车人数每增加500人,每月的利润可增加1000元,
当每月的乘车人数为2000人时,每月利润为0元,则当每月乘车人数为3500人时,每月利润为3000元;
(4)由表中数据可知,每月的乘车人数每增加500人,每月的利润可增加1000元,
当每月的乘车人数为2000人时,每月利润为0元,则当每月利润为5000元时,每月乘车人数为4500人,
故答案为4500.
一.选择题
1.下列图象中,y不是x的函数的是( )
A. B.
C. D.
2.下列式子中,y不是x的函数的是( )
A.y=x2 B.y= C.y= D.y=±
3.在行进路程s、速度v和时间t的相关计算中,若保持行驶的路程不变,则下列说法正确的是( )
A.速度v是变量
B.时间t是变量
C.速度v和时间t都是变量
D.速度v、时间t、路程s都是常量
4.已知声音在空气中的传播速度与空气的温度有关,在一定范围内,其关系如表所示,下列说法错误的是( )
温度/℃ ﹣20 ﹣10 0 10 20 30
传播速度/m/s 318 324 330 336 342 348
A.自变量是温度,因变量是传播速度
B.温度越高,传播速度越快
C.当温度为10℃时,声音5s可以传播1650m
D.温度每升高10℃,传播速度增加6m/s
5.函数y=中自变量x的取值范围是( )
A.x≠0 B.x≥2或x≠0 C.x≥2 D.x≤﹣2且x≠0
6.在函数y=+x﹣2中,自变量x的取值范围是( )
A.x≥﹣4 B.x≠0 C.x≥﹣4且x≠0 D.x>﹣4且x≠0
7.下列函数中,自变量的取值范围不是x≠1的是( )
A.y= B.y=(x﹣1)﹣1 C.y=(x﹣1)0 D.y=2x﹣1
8.函数y=中自变量x的取值范围在数轴上表示正确的是( )
A. B.
C. D.
9.根据图中的程序计算y的值,若输入的x值为3,则输出的y值为( )
A.﹣5 B.5 C. D.4
10.如图是用程序计算函数值,若输入x=3,y=2,则输出的k的值为( )
A. B.6 C. D.
11.小华同学喜欢锻炼,周六他先从家跑步到新华公园,在那里与同学打一会羽毛球后又步行回家,下面能反映小华离家距离y与所用时间x之间关系的图象是( )
A. B.
C. D.
12.某地区用电量与应缴电费之间的关系如下表:则下列叙述错误的是( )
用电量(千瓦?时) 1 2 3 4 …
应缴电费(元) 0.55 1.10 1.65 2.20 …
A.用电量每增加1千瓦?时,电费增加0.55元
B.若用电量为8千瓦?时,则应缴电费4.4元
C.若应缴电费为2.75元,则用电量为6千瓦?时
D.应缴电费随用电量的增加而增加
二.填空题
13.已知y=kx+b,其中y,k,x均不等于零,用y,b,x表示k,则k= .
14.下列:①y=x2;②y=2x+1;③y2=2x(x≥0);④y=(x≥0),具有函数关系(自变量为x)的是 .
15.小亮拿15元钱去文具店买签字笔,每支1.5元,小亮买签字笔后所剩钱数y(元)与买签字笔的支数x(支)之间的关系式为 .
16.函数y=中,自变量的取值范围是 .
17.下表中y与x的数据满足我们初中学过的某种函数关系.其函数表达式为 .
x … ﹣1 0 1 3 …
y … 0 3 4 0 …
三.解答题
18.在一次实验中,小强把一根弹簧的上端固定,在其下端悬挂物体.下面是他测得的弹簧的长度y与所挂物体的质量x的一组对应值:
所挂物体的质量x/kg 0 1 2 3 4 5
弹簧的长度y/cm 20 22 24 26 28 30
(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)填空:
①当所挂的物体为3kg时,弹簧长是 .不挂重物时,弹簧长是 .
②当所挂物体的质量为8kg(在弹簧的弹性限度范围内)时,弹簧长度是 .
19.如图所示,在△ABC中,底边BC=8cm,高AD=6cm,E为AD上一动点,当点E从点D向点A运动时,△BEC的面积发生了变化.
(1)在这个变化过程中,自变量和因变量各是什么?
(2)若设DE长为x(cm),△BEC的面积为y,求y与x之间的关系式.
(3)当DE长度为3cm时,△BEC的面积y是多少?
20.求下列函数中自变量x的取值范围.
(1)y=3x﹣1;
(2)y=+;
(3)y=.
21.已知y=(a﹣1)x+2a﹣4,当x=﹣1时,y=0.
(1)求a的值;
(2)当x=1时,求y的值.
22.某公交车每月的支出费用为4000元,每月的乘车人数x(人)与每月利润(利润=收入费用﹣支出费用)y(元)的变化关系如下表所示(每位乘客的公交票价是固定不变的):
x(人) 500 1000 1500 2000 2500 3000 …
y(元) ﹣3000 ﹣2000 ﹣1000 0 1000 2000 …
(1)在这个变化过程中, 是自变量, 是因变量;
(2)观察表中数据可知,每月乘客量达到 人以上时,该公交车才不会亏损;
(3)请你估计当每月乘车人数为3500人时,每月利润为多少元?
(4)若5月份想获得利润5000元,则请你估计5月份的乘客量需达 人.
参考答案
一.选择题
1. C.
2. D.
3. C.
4. C.
5. C.
6. C.
7. D.
8. C.
9. B.
10. B.
11. B.
12. C.
二.填空题
13. .
14.①②.
15. y=15﹣1.5x.
16. x≥1且x≠3.
17. y=﹣x2+2x+3.
三.解答题
18.(1)反映了弹簧长度y与所挂物体质量x之间的关系,所挂物体的质量是自变量,弹簧的长度是因变量;
(2)①根据表格可知:当所挂物体重量为3千克时,弹簧长度为26cm;不挂重物时,弹簧长度为10cm;
故答案为:26cm 20cm.
②根据表格可知:所挂重物每增加1千克,弹簧增长2cm,根据弹簧的长度=弹簧原来的长度+弹簧伸长的长度可知当所挂物体的重量为x千克时,弹簧长度y=2x+20,将x=8代入得y=2×8+20=36.
故答案为:36cm.
19.(1)在这个变化过程中,自变量为DE的长,因变量是△BEC的面积;
(2)y=×BC×DE=4x(0≤x≤6);
(3)当x=3时,y=4×3=12(cm2).
20.(1)x是任意实数;
(2)根据题意得:,
解得:x≥2且x≠3;
(3)根据题意得:x﹣1≠0,
解得:x≠1.
21.(1)由y=(a﹣1)x+2a﹣4,当x=﹣1时,y=0,得
﹣(a﹣1)+2a﹣4=0,
解得a=3;
(2)函数解析式为y=2x+2,
当x=1时,y=2+2=4.
22.(1)在这个变化过程中,每月的乘车人数x是自变量,每月的利润y是因变量;
故答案为每月的乘车人数x,每月的利润y;
(2)观察表中数据可知,每月乘客量达到观察表中数据可知,每月乘客量达到2000人以上时,该公交车才不会亏损;
故答案为2000;
(3)由表中数据可知,每月的乘车人数每增加500人,每月的利润可增加1000元,
当每月的乘车人数为2000人时,每月利润为0元,则当每月乘车人数为3500人时,每月利润为3000元;
(4)由表中数据可知,每月的乘车人数每增加500人,每月的利润可增加1000元,
当每月的乘车人数为2000人时,每月利润为0元,则当每月利润为5000元时,每月乘车人数为4500人,
故答案为4500.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
