正态分布
图片预览


文档简介
(共26张PPT)
蒋瑞源 105012007126
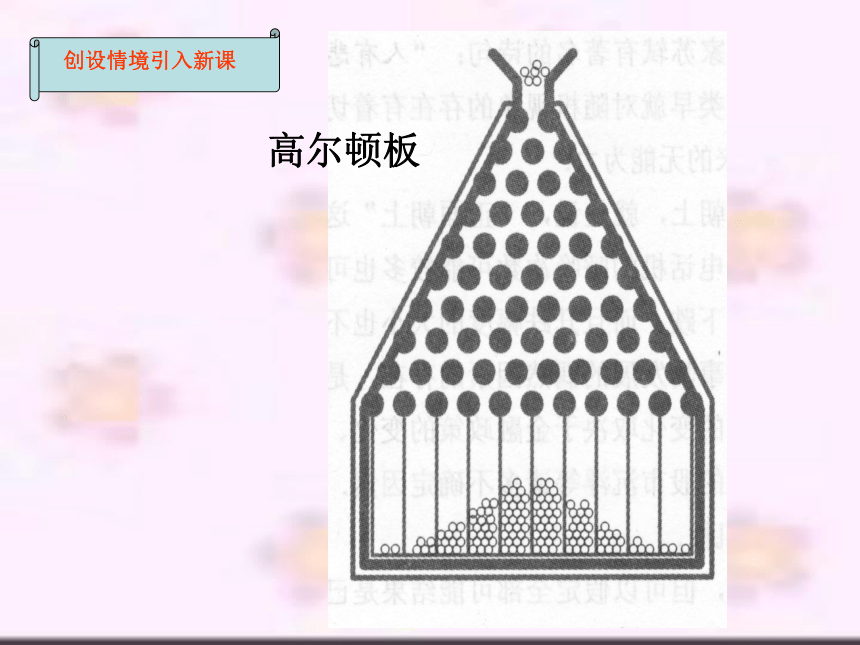
高尔顿板
创设情境引入新课
11
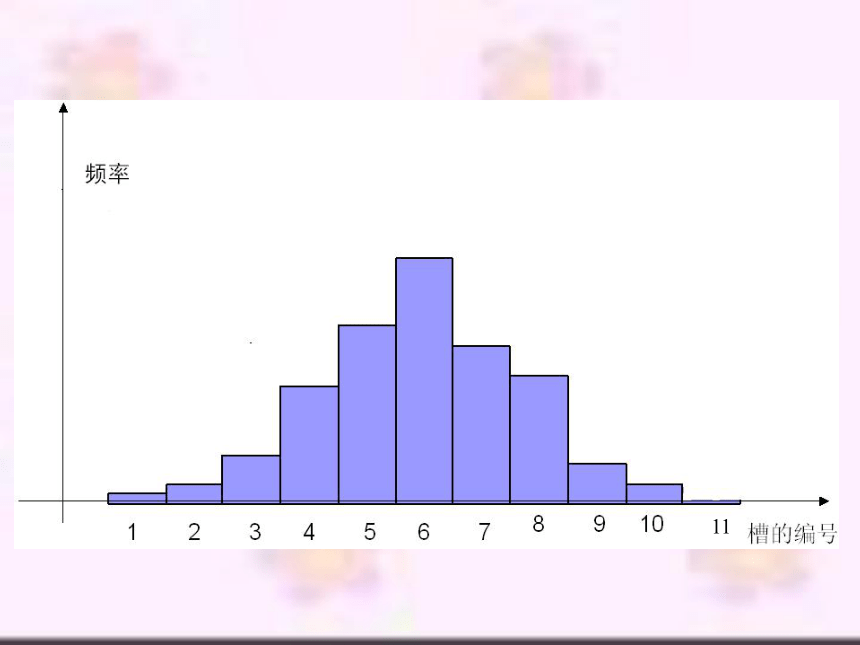
频率
槽的编号
a
b
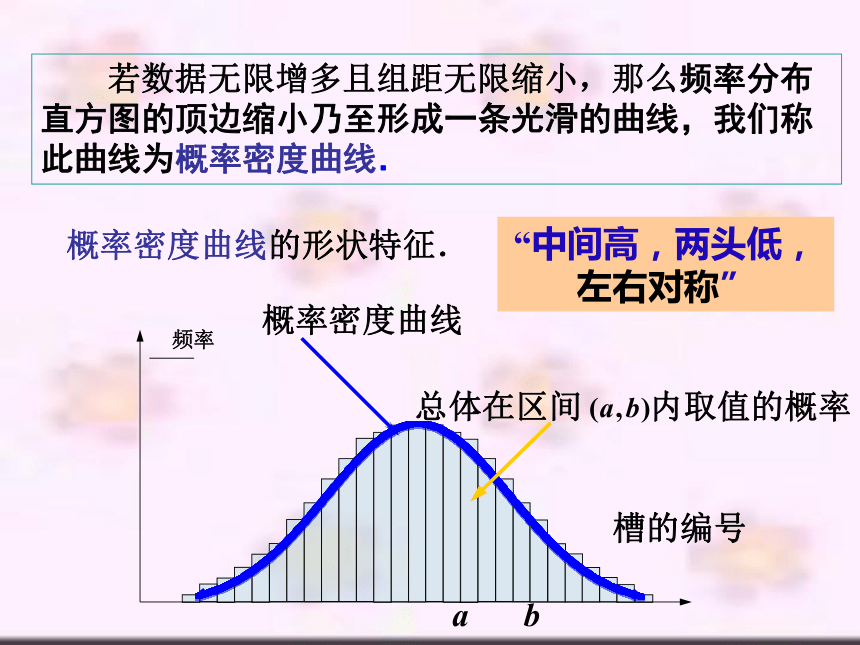
若数据无限增多且组距无限缩小,那么频率分布直方图的顶边缩小乃至形成一条光滑的曲线,我们称此曲线为概率密度曲线.
总体在区间 内取值的概率
概率密度曲线
概率密度曲线的形状特征.
“中间高,两头低,
左右对称”
上图中概率密度曲线具有“中间高,两头低”的特征,像这种类型的概率密度曲线,叫做“正态密度曲线”,它的函数表达式是
式中的实数 、 是参数,分别表示总体的平均数与标准差.不同的 对应着不同的正态密度曲线
)
0
(
>
s
s
知识点一:正态密度曲线的概念
探究新知
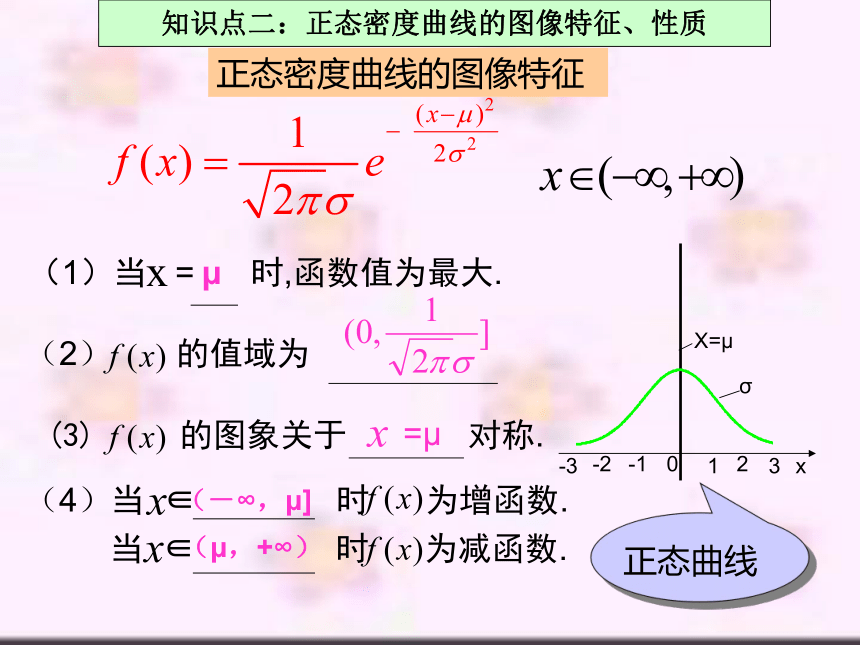
(1)当 = 时,函数值为最大.
(3) 的图象关于 对称.
(2) 的值域为
(4)当 ∈ 时 为增函数.
当 ∈ 时 为减函数.
正态密度曲线的图像特征
μ
(-∞,μ]
(μ,+∞)
0
1
2
-1
-2
x
-3
3
X=μ
σ
正态曲线
=μ
知识点二:正态密度曲线的图像特征、性质
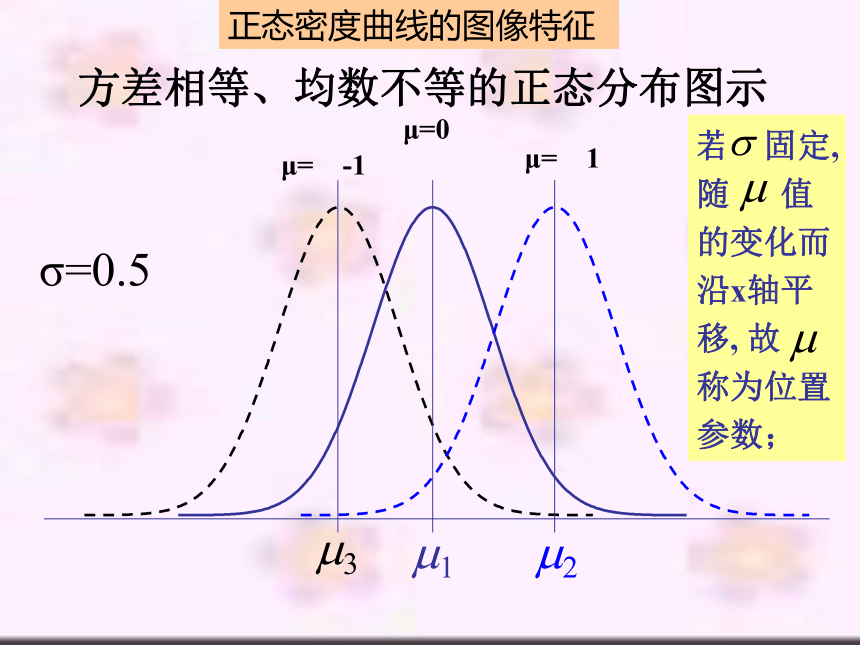
方差相等、均数不等的正态分布图示
3
1
2
σ=0.5
μ= -1
μ=0
μ= 1
若 固定, 随 值的变化而沿x轴平移, 故 称为位置参数;
正态密度曲线的图像特征
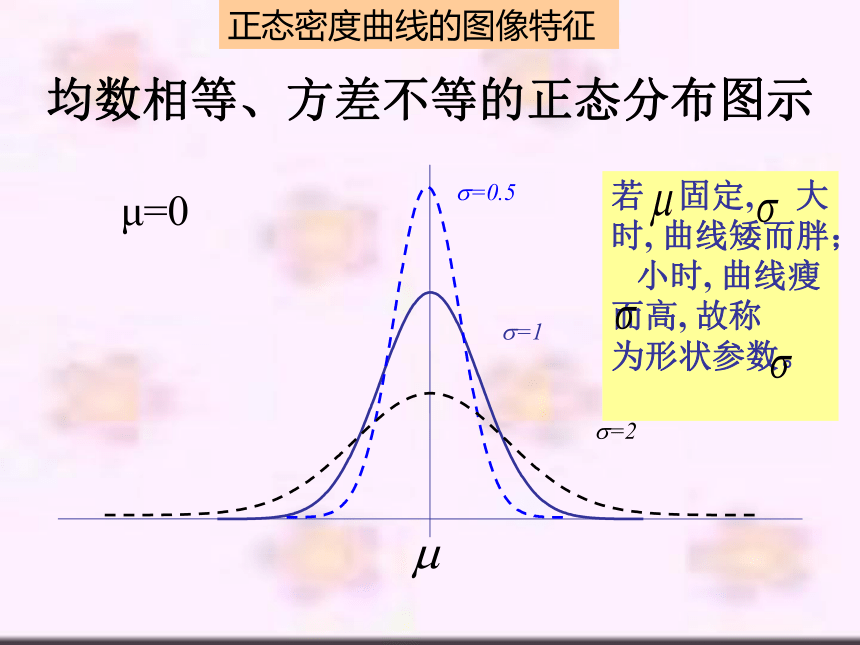
均数相等、方差不等的正态分布图示
=0.5
=1
=2
μ=0
若 固定, 大时, 曲线矮而胖;
小时, 曲线瘦而高, 故称
为形状参数。
正态密度曲线的图像特征
0
1
2
-1
-2
x
y
-3
μ= -1
σ=0.5
0
1
2
-1
-2
x
y
-3
3
μ=0
σ=1
0
1
2
-1
-2
x
y
-3
3
4
μ=1
σ=2
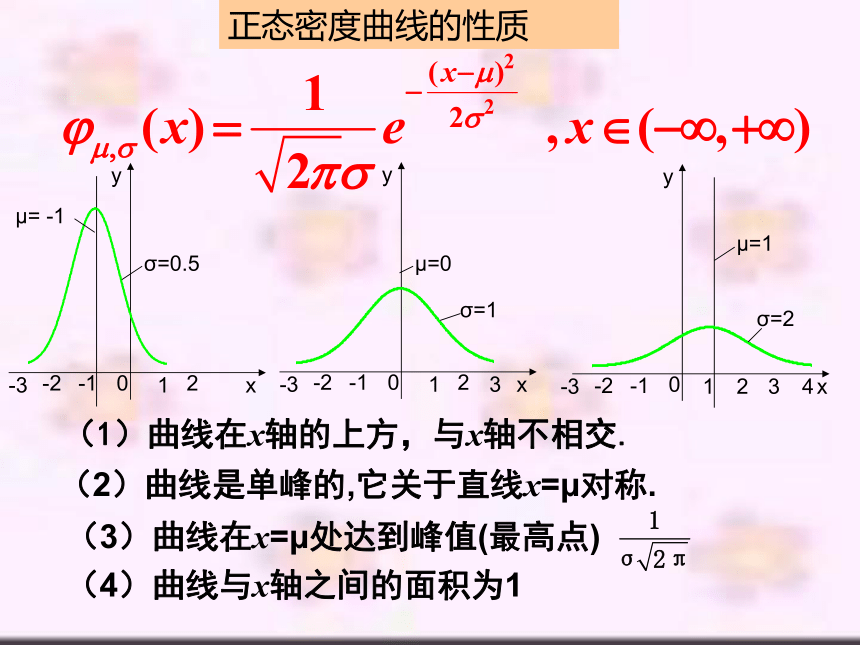
(1)曲线在x轴的上方,与x轴不相交.
(2)曲线是单峰的,它关于直线x=μ对称.
(4)曲线与x轴之间的面积为1
(3)曲线在x=μ处达到峰值(最高点)
正态密度曲线的性质
σ=0.5
0
1
2
-1
-2
x
y
-3
3
X=μ
σ=1
σ=2
(6)当μ一定时,曲线的形状由σ确定 .
σ越大,曲线越“矮胖”,表示总体的分布越分散;
σ越小,曲线越“瘦高”,表示总体的分布越集中.
(5)当 x<μ时,曲线上升;当x>μ时,曲线下降.并且当曲线向左、右两边无限延伸时,以x轴为渐近线,向它无限靠近.
正态密度曲线的性质
1、正态曲线下面积的分布规律
正态曲线下面积的意义:正态曲线下一定区间内的面积代表变量值落在该区间的概率。整个曲线下的面积为1,代表总概率为1。
曲线下面积的求法:定积分法和标准正态分布法
知识点三:正态分布
2.正态分布的定义:
如果对于任何实数 a则称为X 的正态分布. 正态分布由参数μ、σ唯一确定.正态分布记作N( μ,σ2).其图象称为正态曲线.
如果随机变量X服从正态分布,
则记作 X~ N( μ,σ2)
a
b
X
Y
当μ=0,σ=1时,正态总体称为标准正态总体,其相应的函数表达式是
其相应的曲线称为标准正态曲线。标准正态总体N(0,1)在正态总体的研究中占有重要地位。任何正态分布的问题均可转化成标准总体分布的概率问题。
知识点四:标准正态曲线
m-a
m+a
x=μ
特别地有
知识点五: 原则
若X~N ,则对于任何实数a>0,概率
为如图中的阴影部分的面积,对于固定的 和 而言,该面积随着 的减少而变大。这说明 越小, 落在区间 的概率越大,即X集中在 周围概率越大。
我们从上图看到,正态总体在 以外取值的概率只有4.6%,在 以外取值的概率只有0.3 %。
由于这些概率值很小(一般不超过5 % ),通常称这些情况 发生为小概率事件。
原则概念
区 间 取值概率
(μ-σ,μ+σ) 68.3%
(μ-2σ,μ+2σ) 95.4%
(μ-3σ,μ+3σ) 99.7%
小概率事件的含义:
发生概率一般不超过5%的事件,即事件在一次试验中几乎不可能发生
小概率事件的含义
在实际遇到的许多随机现象都服从或近似服从正态分布:
在生产中,在正常生产条件下各种产品的质量指标一般都服
从正态分布;
在测量中,测量结果、测量的随机误差都服从正态分布;
在生物学中,同一群体的某一特征都服从正态分布;
……;
在气象中,某地每年七月份的平均气温、平均湿度、降
雨量等,水文中的水位都服从正态分布。
总之,正态分布广泛存在于自然界、生产及科学技术的许多领域中。
正态分布在概率和统计中占有重要地位。
知识点六:正态分布的意义
例1、把一个正态曲线a沿着横轴方向向右移动2个单位,得到新的一条曲线b。下列说法中不正确的是( )
A.曲线b仍然是正态曲线;
B.曲线a和曲线b的最高点的纵坐标相等;
C.以曲线b为概率密度曲线的总体的期望比以曲线a为概率密度曲线的总体的期望大2;
D.以曲线b为概率密度曲线的总体的方差比以曲线a为概率密度曲线的总体的方差大2。
C
例题讲解
例题2 某地区数学考试的成绩服从正态分布,其密度函数曲线如下图:
写出的分布密度函数;
求成绩位于区间 的概率是多少?
求成绩位于区间 的概率是多少?
若该地区有10000名学生参加考试,从理论上讲成绩在76分以上的考生有多少人?
20 40 60 80 100
y
x
O
例题讲解
例3 设正态总体落在区间 和区间 内的概率相等,落在区间 内的概率 为,求该正态总体对应的正态曲线的最高点的坐标。
例题讲解
归纳小结
1 正态总体函数解析式:
0
1
2
-1
-2
x
y
-3
μ= -1
σ=0.5
0
1
2
-1
-2
x
y
-3
3
μ=0
σ=1
0
1
2
-1
-2
x
y
-3
3
4
μ=1
σ=2
2 正态曲线
归纳小结
3 正态曲线的性质
(1)曲线在x轴的上方,与x轴不相交.
(2)曲线关于直线x=μ对称.
(3)曲线在x=μ时位于最高点.
(4)当 x<μ时,曲线上升;当x>μ时,曲线下降.
并且当曲线向左、右两边无限延伸时,以轴为渐近线,
向它无限靠近.
(5)当μ一定时,曲线的形状由σ确定 .
σ越大,曲线越“矮胖”,表示总体的分布越分散;
σ越小,曲线越“瘦高”,表示总体的分布越集中.
归纳小结
4.标准正态分布
a
b
X
Y
(2)“标准正态分布表”
一、 课本75页 A组 第1题
B组 第2题
二、 在某校举行的数学竞赛中,全体参赛学生的竞赛成绩近似服从正态分布 ,已知成绩在90分以上(含90分)的学生有12名。试问此次参赛的学生总数约有多少人?
课外思考:请尝试从解析式角度分析正态
曲线的对称性与最值。
布置作业
谢谢!
蒋瑞源 105012007126
高尔顿板
创设情境引入新课
11
频率
槽的编号
a
b
若数据无限增多且组距无限缩小,那么频率分布直方图的顶边缩小乃至形成一条光滑的曲线,我们称此曲线为概率密度曲线.
总体在区间 内取值的概率
概率密度曲线
概率密度曲线的形状特征.
“中间高,两头低,
左右对称”
上图中概率密度曲线具有“中间高,两头低”的特征,像这种类型的概率密度曲线,叫做“正态密度曲线”,它的函数表达式是
式中的实数 、 是参数,分别表示总体的平均数与标准差.不同的 对应着不同的正态密度曲线
)
0
(
>
s
s
知识点一:正态密度曲线的概念
探究新知
(1)当 = 时,函数值为最大.
(3) 的图象关于 对称.
(2) 的值域为
(4)当 ∈ 时 为增函数.
当 ∈ 时 为减函数.
正态密度曲线的图像特征
μ
(-∞,μ]
(μ,+∞)
0
1
2
-1
-2
x
-3
3
X=μ
σ
正态曲线
=μ
知识点二:正态密度曲线的图像特征、性质
方差相等、均数不等的正态分布图示
3
1
2
σ=0.5
μ= -1
μ=0
μ= 1
若 固定, 随 值的变化而沿x轴平移, 故 称为位置参数;
正态密度曲线的图像特征
均数相等、方差不等的正态分布图示
=0.5
=1
=2
μ=0
若 固定, 大时, 曲线矮而胖;
小时, 曲线瘦而高, 故称
为形状参数。
正态密度曲线的图像特征
0
1
2
-1
-2
x
y
-3
μ= -1
σ=0.5
0
1
2
-1
-2
x
y
-3
3
μ=0
σ=1
0
1
2
-1
-2
x
y
-3
3
4
μ=1
σ=2
(1)曲线在x轴的上方,与x轴不相交.
(2)曲线是单峰的,它关于直线x=μ对称.
(4)曲线与x轴之间的面积为1
(3)曲线在x=μ处达到峰值(最高点)
正态密度曲线的性质
σ=0.5
0
1
2
-1
-2
x
y
-3
3
X=μ
σ=1
σ=2
(6)当μ一定时,曲线的形状由σ确定 .
σ越大,曲线越“矮胖”,表示总体的分布越分散;
σ越小,曲线越“瘦高”,表示总体的分布越集中.
(5)当 x<μ时,曲线上升;当x>μ时,曲线下降.并且当曲线向左、右两边无限延伸时,以x轴为渐近线,向它无限靠近.
正态密度曲线的性质
1、正态曲线下面积的分布规律
正态曲线下面积的意义:正态曲线下一定区间内的面积代表变量值落在该区间的概率。整个曲线下的面积为1,代表总概率为1。
曲线下面积的求法:定积分法和标准正态分布法
知识点三:正态分布
2.正态分布的定义:
如果对于任何实数 a
如果随机变量X服从正态分布,
则记作 X~ N( μ,σ2)
a
b
X
Y
当μ=0,σ=1时,正态总体称为标准正态总体,其相应的函数表达式是
其相应的曲线称为标准正态曲线。标准正态总体N(0,1)在正态总体的研究中占有重要地位。任何正态分布的问题均可转化成标准总体分布的概率问题。
知识点四:标准正态曲线
m-a
m+a
x=μ
特别地有
知识点五: 原则
若X~N ,则对于任何实数a>0,概率
为如图中的阴影部分的面积,对于固定的 和 而言,该面积随着 的减少而变大。这说明 越小, 落在区间 的概率越大,即X集中在 周围概率越大。
我们从上图看到,正态总体在 以外取值的概率只有4.6%,在 以外取值的概率只有0.3 %。
由于这些概率值很小(一般不超过5 % ),通常称这些情况 发生为小概率事件。
原则概念
区 间 取值概率
(μ-σ,μ+σ) 68.3%
(μ-2σ,μ+2σ) 95.4%
(μ-3σ,μ+3σ) 99.7%
小概率事件的含义:
发生概率一般不超过5%的事件,即事件在一次试验中几乎不可能发生
小概率事件的含义
在实际遇到的许多随机现象都服从或近似服从正态分布:
在生产中,在正常生产条件下各种产品的质量指标一般都服
从正态分布;
在测量中,测量结果、测量的随机误差都服从正态分布;
在生物学中,同一群体的某一特征都服从正态分布;
……;
在气象中,某地每年七月份的平均气温、平均湿度、降
雨量等,水文中的水位都服从正态分布。
总之,正态分布广泛存在于自然界、生产及科学技术的许多领域中。
正态分布在概率和统计中占有重要地位。
知识点六:正态分布的意义
例1、把一个正态曲线a沿着横轴方向向右移动2个单位,得到新的一条曲线b。下列说法中不正确的是( )
A.曲线b仍然是正态曲线;
B.曲线a和曲线b的最高点的纵坐标相等;
C.以曲线b为概率密度曲线的总体的期望比以曲线a为概率密度曲线的总体的期望大2;
D.以曲线b为概率密度曲线的总体的方差比以曲线a为概率密度曲线的总体的方差大2。
C
例题讲解
例题2 某地区数学考试的成绩服从正态分布,其密度函数曲线如下图:
写出的分布密度函数;
求成绩位于区间 的概率是多少?
求成绩位于区间 的概率是多少?
若该地区有10000名学生参加考试,从理论上讲成绩在76分以上的考生有多少人?
20 40 60 80 100
y
x
O
例题讲解
例3 设正态总体落在区间 和区间 内的概率相等,落在区间 内的概率 为,求该正态总体对应的正态曲线的最高点的坐标。
例题讲解
归纳小结
1 正态总体函数解析式:
0
1
2
-1
-2
x
y
-3
μ= -1
σ=0.5
0
1
2
-1
-2
x
y
-3
3
μ=0
σ=1
0
1
2
-1
-2
x
y
-3
3
4
μ=1
σ=2
2 正态曲线
归纳小结
3 正态曲线的性质
(1)曲线在x轴的上方,与x轴不相交.
(2)曲线关于直线x=μ对称.
(3)曲线在x=μ时位于最高点.
(4)当 x<μ时,曲线上升;当x>μ时,曲线下降.
并且当曲线向左、右两边无限延伸时,以轴为渐近线,
向它无限靠近.
(5)当μ一定时,曲线的形状由σ确定 .
σ越大,曲线越“矮胖”,表示总体的分布越分散;
σ越小,曲线越“瘦高”,表示总体的分布越集中.
归纳小结
4.标准正态分布
a
b
X
Y
(2)“标准正态分布表”
一、 课本75页 A组 第1题
B组 第2题
二、 在某校举行的数学竞赛中,全体参赛学生的竞赛成绩近似服从正态分布 ,已知成绩在90分以上(含90分)的学生有12名。试问此次参赛的学生总数约有多少人?
课外思考:请尝试从解析式角度分析正态
曲线的对称性与最值。
布置作业
谢谢!
