二分法求函数零点的近似值
图片预览


文档简介
§2.4.2用二分法求函数的零点
[教学目标]
(1)知识与技能
通过具体实例理解二分法的概念及其适用条件、实施步骤,了解二分法是求函数零点近似解的常用方法,从中体会函数与方程之间的联系及其在实际问题中的应用.
(2)过程与方法
通过对例题的探究、解法展示与交流,体会函数单调性、值域、图象在函数零点的定性研究中的运用;
在二分法概念的形成过程中,巩固函数零点判定定理(布尔查诺定理);
能借助计算器,用二分法求函数零点的近似解,并感受其中所蕴含的的算法思想.
(3)情感、态度、价值观
从生活经验上升到数学方法,感受数学与自然、社会的和谐与美妙;
体会数学逼近过程,感受精确与近似的相对统一.
[重点] 学会用二分法求函数的零点
[难点] 理解用二分法求函数零点的原理
[教学方式]合作探究、启发式、课后自主探究
[教学媒体]多功能展示台,几何画板4.06中文版、Microsoft Excel
[教学流程]
→
[教学过程]
一、创设情境
问题1:有新款手机价格在4000~8000元之间,请你猜其价格?
投影打出问题,链接展示小课件
问题1的设计意图:互动,兴趣引入,领会“逐步缩小区间,逼近准确值”的朴素的想法.
问题2:解方程
思路1:着眼于“数”,进行等式变形,如因式分解,配方
思路2:着眼于“数”,试图代公式或者寻求公式,模式识别
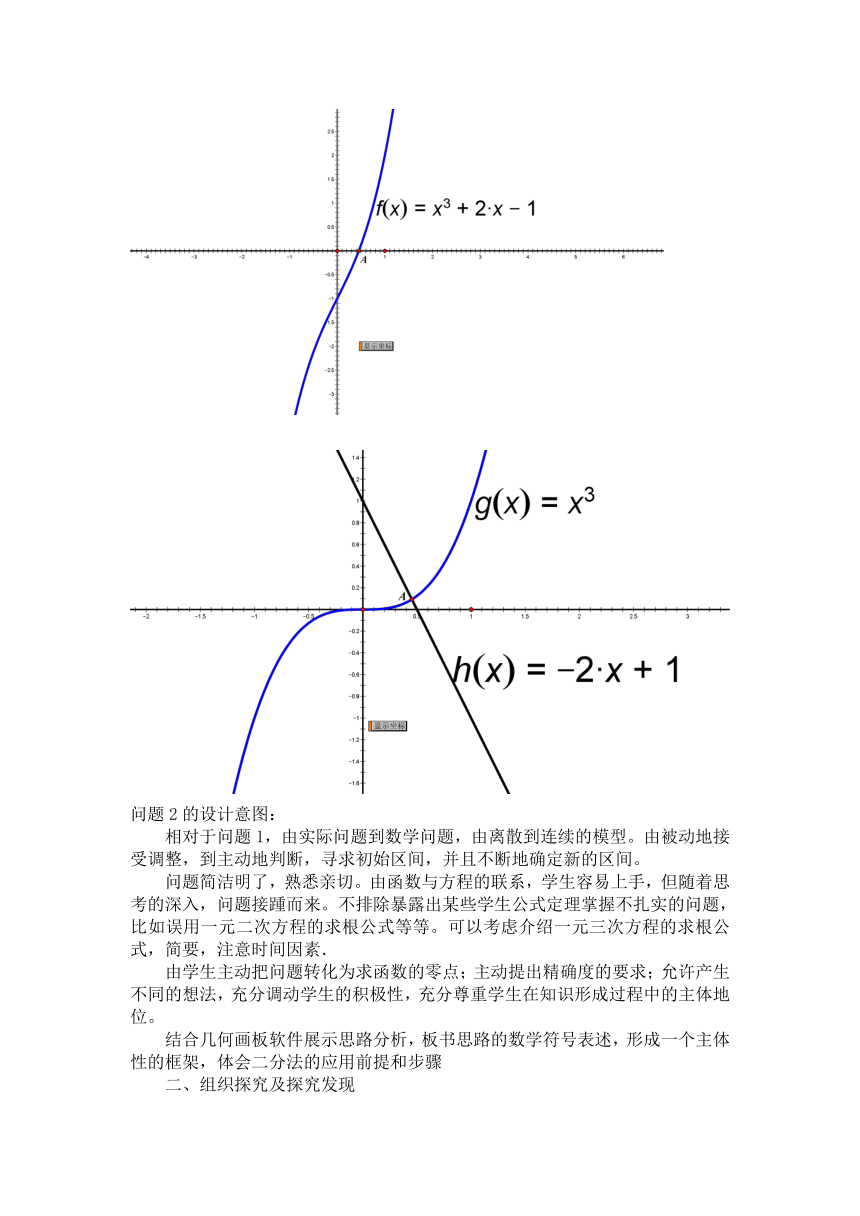
思路3:着眼于“形”,形数结合,转化为函数的零点,运用函数的性质进行根的存在性探索,并且,进一步地, 从定性研究到定量的细致入微的研究
问题2的设计意图:
相对于问题1,由实际问题到数学问题,由离散到连续的模型。由被动地接受调整,到主动地判断,寻求初始区间,并且不断地确定新的区间。
问题简洁明了,熟悉亲切。由函数与方程的联系,学生容易上手,但随着思考的深入,问题接踵而来。不排除暴露出某些学生公式定理掌握不扎实的问题,比如误用一元二次方程的求根公式等等。可以考虑介绍一元三次方程的求根公式,简要,注意时间因素.
由学生主动把问题转化为求函数的零点;主动提出精确度的要求;允许产生不同的想法,充分调动学生的积极性,充分尊重学生在知识形成过程中的主体地位。
结合几何画板软件展示思路分析,板书思路的数学符号表述,形成一个主体性的框架,体会二分法的应用前提和步骤
二、组织探究及探究发现
探究问题1:前面问题求解方法,称为二分法,归纳较为严格的表述.
二分法:对于在区间,上连续不断,且满足·的函数,通过不断地把函数的零点所在的区间一分为二,使区间的两个端点逐步逼近零点,进而得到零点近似值的方法叫做二分法.
探究问题2:二分法的一般步骤是什么
给定精度,用二分法求函数的零点近似值的步骤如下:
1.确定区间,,验证·,给定精度;
2.求区间,的中点;
3.计算:
若=,则就是函数的零点;
若·<,则令=(此时零点);
若·<,则令=(此时零点);
4.判断是否达到精度;
即若,则得到零点值(或);否则重复步骤2~4.
练习1、用二分法求函数的一个正的零点,可以作为计算的初始区间的是( C )
(A) [,1] (B)[0,1] (C)[1,2] (D)[2,3]
练习2、用二分法求函数的一个零点时,若取区间[2,3]为计算的初始区间,则下一个区间应取为_______________答:
练习1,2的设计意图:以上两个小题的思考难度小,但是有利于学生形成或者是顺应规范的二分法步骤,题目也有检查二分法使用的前提条件的功用.
例.求函数的零点的近似值(精确到0.1)
先分析,再求解
小组协作,借助计算器完成
逐步计算,完成表格
端点或中点横坐标 计算端点或中点的函数值 确定区间
a=0,b=1 f(0)=-1<0,f(1)=2>0 [0,1]
c=(0+1)/2=0.5
由上表的计算可知,所求的近似值是______.
三、问题的反思与发展
上面的问题中,如果精确度要求更高,比如精确到0.001,必然要接着算好多步,面对这些渐渐不可爱的数字,我们很容易想到,能不能把以上大量的重复计算这些力气活交给机器完成?那么,怎样给计算工具交待任务?——把问题的算法步骤提炼出来→编写程序→机器执行→分析、利用结果进行进一步的研究
探究问题3:能否根据二分法的步骤列出图解示意图(渗透算法思想)
四、学习小结:1、知识方面:二分法(适用范围、步骤)
2、思想方法:数形结合、无限逼近、算法思想
3、疑惑:
五、课后实践
练习1:在利用二分法求的近似解过程中,有,, 则其近似解落在区间 .
练习2:求函数的一个正实数零点(精确到0.1).
练习3:已知函数的图象如下,能否用二分法求零点的近似值?
练习4:有12个大小相同的小球,其中有11个小球质量相等,另有一个小球稍重,用天平称几次就可以找出这个稍重的球?
课外拓展1:利用网络或书籍查找有关高次方程的研究史料.
课外拓展2:利用二分法的图解示意图,结合所学的计算机语言编出求解函数零点的程序(对数学基础较好和计算机较好的同学提出要求).
巩固与发展
课外实践
探索发现
组织探究
创设情境
[教学目标]
(1)知识与技能
通过具体实例理解二分法的概念及其适用条件、实施步骤,了解二分法是求函数零点近似解的常用方法,从中体会函数与方程之间的联系及其在实际问题中的应用.
(2)过程与方法
通过对例题的探究、解法展示与交流,体会函数单调性、值域、图象在函数零点的定性研究中的运用;
在二分法概念的形成过程中,巩固函数零点判定定理(布尔查诺定理);
能借助计算器,用二分法求函数零点的近似解,并感受其中所蕴含的的算法思想.
(3)情感、态度、价值观
从生活经验上升到数学方法,感受数学与自然、社会的和谐与美妙;
体会数学逼近过程,感受精确与近似的相对统一.
[重点] 学会用二分法求函数的零点
[难点] 理解用二分法求函数零点的原理
[教学方式]合作探究、启发式、课后自主探究
[教学媒体]多功能展示台,几何画板4.06中文版、Microsoft Excel
[教学流程]
→
[教学过程]
一、创设情境
问题1:有新款手机价格在4000~8000元之间,请你猜其价格?
投影打出问题,链接展示小课件
问题1的设计意图:互动,兴趣引入,领会“逐步缩小区间,逼近准确值”的朴素的想法.
问题2:解方程
思路1:着眼于“数”,进行等式变形,如因式分解,配方
思路2:着眼于“数”,试图代公式或者寻求公式,模式识别
思路3:着眼于“形”,形数结合,转化为函数的零点,运用函数的性质进行根的存在性探索,并且,进一步地, 从定性研究到定量的细致入微的研究
问题2的设计意图:
相对于问题1,由实际问题到数学问题,由离散到连续的模型。由被动地接受调整,到主动地判断,寻求初始区间,并且不断地确定新的区间。
问题简洁明了,熟悉亲切。由函数与方程的联系,学生容易上手,但随着思考的深入,问题接踵而来。不排除暴露出某些学生公式定理掌握不扎实的问题,比如误用一元二次方程的求根公式等等。可以考虑介绍一元三次方程的求根公式,简要,注意时间因素.
由学生主动把问题转化为求函数的零点;主动提出精确度的要求;允许产生不同的想法,充分调动学生的积极性,充分尊重学生在知识形成过程中的主体地位。
结合几何画板软件展示思路分析,板书思路的数学符号表述,形成一个主体性的框架,体会二分法的应用前提和步骤
二、组织探究及探究发现
探究问题1:前面问题求解方法,称为二分法,归纳较为严格的表述.
二分法:对于在区间,上连续不断,且满足·的函数,通过不断地把函数的零点所在的区间一分为二,使区间的两个端点逐步逼近零点,进而得到零点近似值的方法叫做二分法.
探究问题2:二分法的一般步骤是什么
给定精度,用二分法求函数的零点近似值的步骤如下:
1.确定区间,,验证·,给定精度;
2.求区间,的中点;
3.计算:
若=,则就是函数的零点;
若·<,则令=(此时零点);
若·<,则令=(此时零点);
4.判断是否达到精度;
即若,则得到零点值(或);否则重复步骤2~4.
练习1、用二分法求函数的一个正的零点,可以作为计算的初始区间的是( C )
(A) [,1] (B)[0,1] (C)[1,2] (D)[2,3]
练习2、用二分法求函数的一个零点时,若取区间[2,3]为计算的初始区间,则下一个区间应取为_______________答:
练习1,2的设计意图:以上两个小题的思考难度小,但是有利于学生形成或者是顺应规范的二分法步骤,题目也有检查二分法使用的前提条件的功用.
例.求函数的零点的近似值(精确到0.1)
先分析,再求解
小组协作,借助计算器完成
逐步计算,完成表格
端点或中点横坐标 计算端点或中点的函数值 确定区间
a=0,b=1 f(0)=-1<0,f(1)=2>0 [0,1]
c=(0+1)/2=0.5
由上表的计算可知,所求的近似值是______.
三、问题的反思与发展
上面的问题中,如果精确度要求更高,比如精确到0.001,必然要接着算好多步,面对这些渐渐不可爱的数字,我们很容易想到,能不能把以上大量的重复计算这些力气活交给机器完成?那么,怎样给计算工具交待任务?——把问题的算法步骤提炼出来→编写程序→机器执行→分析、利用结果进行进一步的研究
探究问题3:能否根据二分法的步骤列出图解示意图(渗透算法思想)
四、学习小结:1、知识方面:二分法(适用范围、步骤)
2、思想方法:数形结合、无限逼近、算法思想
3、疑惑:
五、课后实践
练习1:在利用二分法求的近似解过程中,有,, 则其近似解落在区间 .
练习2:求函数的一个正实数零点(精确到0.1).
练习3:已知函数的图象如下,能否用二分法求零点的近似值?
练习4:有12个大小相同的小球,其中有11个小球质量相等,另有一个小球稍重,用天平称几次就可以找出这个稍重的球?
课外拓展1:利用网络或书籍查找有关高次方程的研究史料.
课外拓展2:利用二分法的图解示意图,结合所学的计算机语言编出求解函数零点的程序(对数学基础较好和计算机较好的同学提出要求).
巩固与发展
课外实践
探索发现
组织探究
创设情境
