2012优化方案数学精品课件(新人教A版选修2-3):第1章优化总结
文档属性
| 名称 | 2012优化方案数学精品课件(新人教A版选修2-3):第1章优化总结 |

|
|
| 格式 | rar | ||
| 文件大小 | 347.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-10-20 00:00:00 | ||
图片预览







文档简介
(共26张PPT)
本章优化总结
专题探究精讲
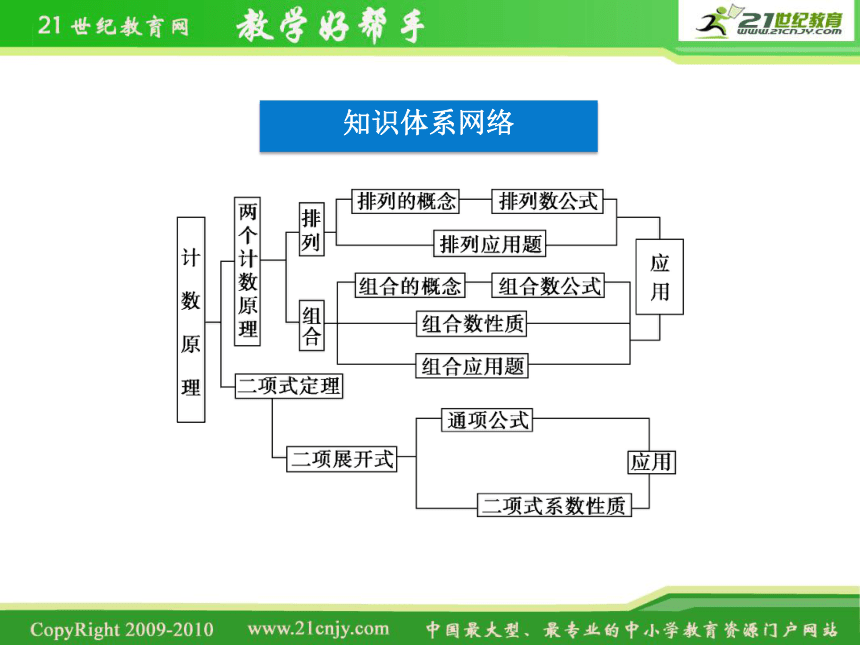
知识体系网络
本章优化总结
知识体系网络
专题探究精讲
基本原理的应用技巧
基本原理提供了“完成某件事情”是“分类”进行,还是“分步”进行.在分类或分步中,针对具体问题考虑是与“顺序”有关,还是无关,来确定排列与组合.
优 化
方 案
现有4种不同颜色要对如图所示的四个部分进行着色,要求有公共边界的两部分不能用同一种颜色,则不同的着色方法共有
( )
A.144种 B.72种
C.64种 D.84种
例1
【思路点拨】 涂色问题,一般分类中再分步,此题可按所用颜色的种类分类,也可按不相邻区域的涂法分类.
【答案】 D
【误区警示】 此题易错选为B,其算法为4×3×3×2=72,其原因是分类不清.
排列与组合应用题的技巧
在解决一个实际问题的过程中,常常遇到排列、组合的综合性问题.而解决问题的第一步是审题,只有认真审题,才能把握问题的实质,分清是排列问题、组合问题,还是综合问题,分清分类与分步的标准和方式,并且要遵循两个原则:一是按元素的性质进行分类;二是按事情发生的过程进行分步.
解决排列组合应用题的常用方法:
(1)合理分类,准确分步;
(2)特殊优先,一般在后;
(3)先取后排,间接排除;
(4)集团捆绑,间隔插空;
(5)抽象问题,构造模型;
(6)均分除序,定序除序.
用数字1,2,3,4,5组成没有重复数字的五位数,则其中数字2,3相邻的偶数有________个.(用数字作答)
例2
【解析】 数字2和3相邻的偶数有两种情况.第一种情况,当数字2在个位上时,则3必定在十位上,此时这样的五位数共有6个;第二种情况,当数字4在个位上时,且2,3必须相邻,此时满足要求的五位数有AA=12(个),则一共有6+12=18(个).
【答案】 18
【题后小结】 “个位”是特殊位置或“偶数数字”是特殊元素,应优先考虑.
从1,3,5,7,9五个数字中选2个,0,2,4,6,8五个数字中选3个,能组成多少个无重复数字的五位数?
例3
【题后小结】 对于组合、排列的综合问题,一般采取先取元素后排列的方法.
某校高二年级共有六个班级,现从外地转入4名学生,要安排到该年级的两个班级且每班安排2名,则不同的安排方案种数为( )
A.80 B.90
C.100 D.120
例4
【答案】 B
【题后小结】 本题是平均分组再分配问题.平均分组是组合数除以“组数”的排列数,分配就是排列.
二项式定理的解题技巧
对于二项式定理的考查常有两类问题:第一类,直接运用通项公式求特定项或解决与系数有关的问题;第二类,需运用转化思想化归为二项式定理来处理的问题.
二项式(2+x)n的展开式中,前三项的系数依次为等差数列,则展开式的第8项的系数为________.(用数字作答)
例5
【答案】 16
【题后小结】 本题是用展开式的通项求特定项的系数,区分系数和二项式系数是关键.
已知(1+x)6(1-2x)5=a0+a1x+a2x2+…+a11x11,那么a1+a2+a3+…+a11=________.
【解析】 令x=0,得a0=1;
令x=1,得a0+a1+a2+…+a11=-64;
∴a1+a2+…+a11=-65.
【答案】 -65
【题后小结】 赋值法是求二项式系数和的主要方法.
例6
例7
【答案】 C
【题后小结】 本题各项系数的变化,除注意负号外,还要注意i的运算性质,各项系数的绝对值为二项式系数.
本章优化总结
专题探究精讲
知识体系网络
本章优化总结
知识体系网络
专题探究精讲
基本原理的应用技巧
基本原理提供了“完成某件事情”是“分类”进行,还是“分步”进行.在分类或分步中,针对具体问题考虑是与“顺序”有关,还是无关,来确定排列与组合.
优 化
方 案
现有4种不同颜色要对如图所示的四个部分进行着色,要求有公共边界的两部分不能用同一种颜色,则不同的着色方法共有
( )
A.144种 B.72种
C.64种 D.84种
例1
【思路点拨】 涂色问题,一般分类中再分步,此题可按所用颜色的种类分类,也可按不相邻区域的涂法分类.
【答案】 D
【误区警示】 此题易错选为B,其算法为4×3×3×2=72,其原因是分类不清.
排列与组合应用题的技巧
在解决一个实际问题的过程中,常常遇到排列、组合的综合性问题.而解决问题的第一步是审题,只有认真审题,才能把握问题的实质,分清是排列问题、组合问题,还是综合问题,分清分类与分步的标准和方式,并且要遵循两个原则:一是按元素的性质进行分类;二是按事情发生的过程进行分步.
解决排列组合应用题的常用方法:
(1)合理分类,准确分步;
(2)特殊优先,一般在后;
(3)先取后排,间接排除;
(4)集团捆绑,间隔插空;
(5)抽象问题,构造模型;
(6)均分除序,定序除序.
用数字1,2,3,4,5组成没有重复数字的五位数,则其中数字2,3相邻的偶数有________个.(用数字作答)
例2
【解析】 数字2和3相邻的偶数有两种情况.第一种情况,当数字2在个位上时,则3必定在十位上,此时这样的五位数共有6个;第二种情况,当数字4在个位上时,且2,3必须相邻,此时满足要求的五位数有AA=12(个),则一共有6+12=18(个).
【答案】 18
【题后小结】 “个位”是特殊位置或“偶数数字”是特殊元素,应优先考虑.
从1,3,5,7,9五个数字中选2个,0,2,4,6,8五个数字中选3个,能组成多少个无重复数字的五位数?
例3
【题后小结】 对于组合、排列的综合问题,一般采取先取元素后排列的方法.
某校高二年级共有六个班级,现从外地转入4名学生,要安排到该年级的两个班级且每班安排2名,则不同的安排方案种数为( )
A.80 B.90
C.100 D.120
例4
【答案】 B
【题后小结】 本题是平均分组再分配问题.平均分组是组合数除以“组数”的排列数,分配就是排列.
二项式定理的解题技巧
对于二项式定理的考查常有两类问题:第一类,直接运用通项公式求特定项或解决与系数有关的问题;第二类,需运用转化思想化归为二项式定理来处理的问题.
二项式(2+x)n的展开式中,前三项的系数依次为等差数列,则展开式的第8项的系数为________.(用数字作答)
例5
【答案】 16
【题后小结】 本题是用展开式的通项求特定项的系数,区分系数和二项式系数是关键.
已知(1+x)6(1-2x)5=a0+a1x+a2x2+…+a11x11,那么a1+a2+a3+…+a11=________.
【解析】 令x=0,得a0=1;
令x=1,得a0+a1+a2+…+a11=-64;
∴a1+a2+…+a11=-65.
【答案】 -65
【题后小结】 赋值法是求二项式系数和的主要方法.
例6
例7
【答案】 C
【题后小结】 本题各项系数的变化,除注意负号外,还要注意i的运算性质,各项系数的绝对值为二项式系数.
