湘教版 九年级数学下册 第3章 投影与视图 单元达标测试卷(word版 含答案)
文档属性
| 名称 | 湘教版 九年级数学下册 第3章 投影与视图 单元达标测试卷(word版 含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 126.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-09 00:00:00 | ||
图片预览


文档简介
第3章达标测试卷
一、选择题(每题3分,共24分)
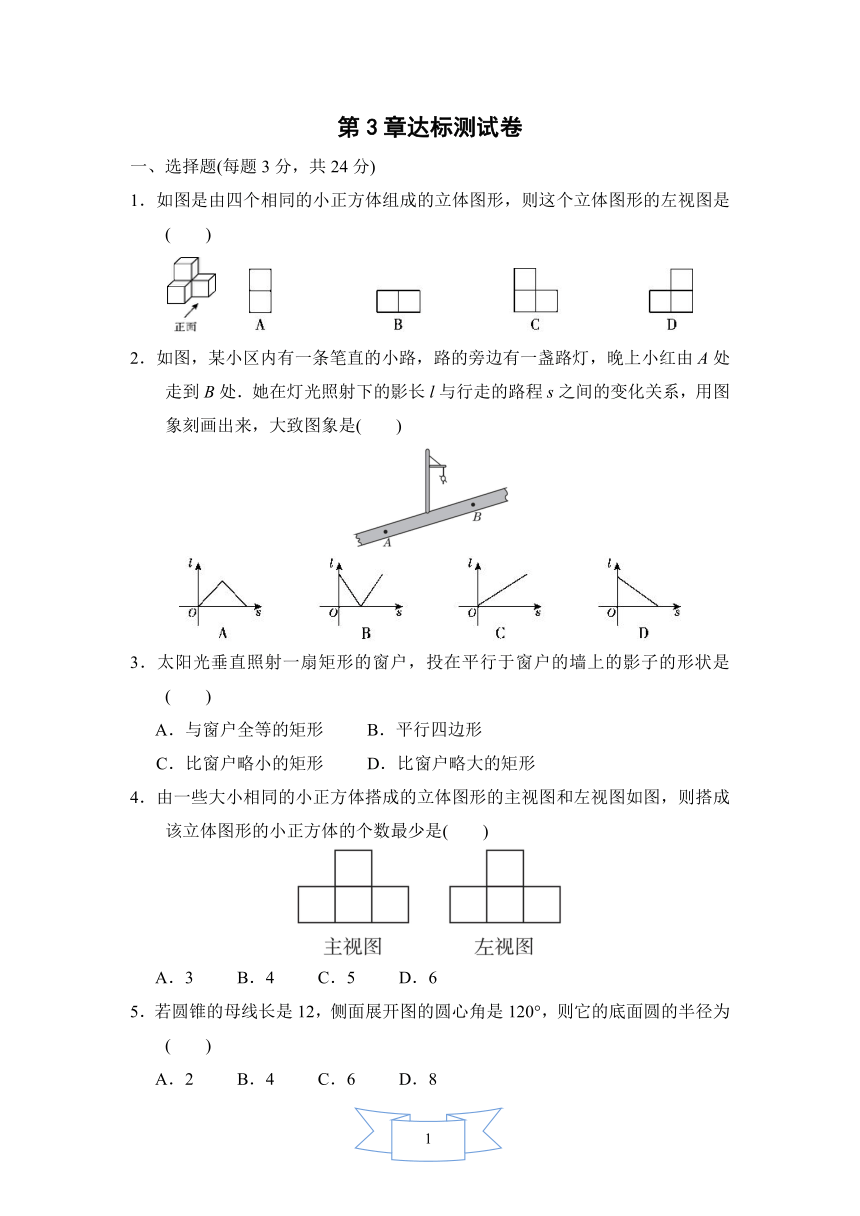
1.如图是由四个相同的小正方体组成的立体图形,则这个立体图形的左视图是( )
2.如图,某小区内有一条笔直的小路,路的旁边有一盏路灯,晚上小红由A处走到B处.她在灯光照射下的影长l与行走的路程s之间的变化关系,用图象刻画出来,大致图象是( )
3.太阳光垂直照射一扇矩形的窗户,投在平行于窗户的墙上的影子的形状是( )
A.与窗户全等的矩形 B.平行四边形
C.比窗户略小的矩形 D.比窗户略大的矩形
4.由一些大小相同的小正方体搭成的立体图形的主视图和左视图如图,则搭成该立体图形的小正方体的个数最少是( )
A.3 B.4 C.5 D.6
5.若圆锥的母线长是12,侧面展开图的圆心角是120°,则它的底面圆的半径为( )
A.2 B.4 C.6 D.8
6.如图,某剧院舞台上的照明灯P射出的光线成“锥体”,其“锥体”面图的“锥角”是60°.已知舞台ABCD是边长为6 m的正方形,O是“锥体”底面圆的圆心.要使灯光能照射到整个舞台,则灯P的悬挂高度是( )
A.3 m B.3 m C.4 m D. m
7.路边有一根电线杆AB和一块正方形广告牌CDFH,在某一时刻,小明发现在太阳光照射下,电线杆顶端A的影子刚好落在HF的中点G处,而正方形广告牌顶端上的F点的影子刚好落在地面上的E点(如图),已知BC=5米,正方形边长为3米,DE=4米,则电线杆的高度约是( )
A.8米 B.7米 C.6米 D.7.9米
8.如图,从一块直径为24 cm的圆形纸片上剪出一个圆心角为90°的扇形ABC,使点A,B,C在圆周上.将剪下的扇形作为一个圆锥的侧面,则这个圆锥的底面圆的半径是( )
A.12 cm B.6 cm
C.3 cm D.2 cm
二、填空题(每题4分,共32分)
9.若一个几何体的主视图、左视图、俯视图都相同,这个几何体可能是________.(写一个即可)
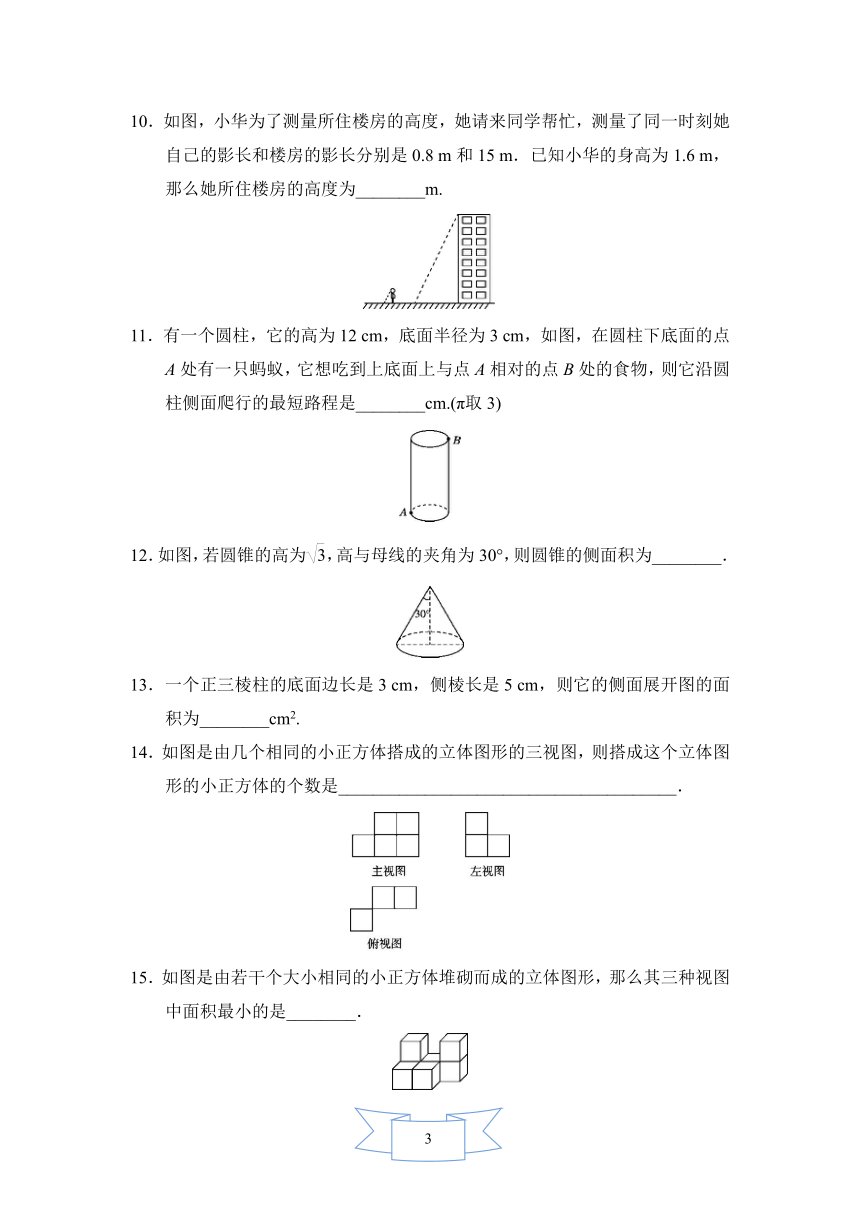
10.如图,小华为了测量所住楼房的高度,她请来同学帮忙,测量了同一时刻她自己的影长和楼房的影长分别是0.8 m和15 m.已知小华的身高为1.6 m,那么她所住楼房的高度为________m.
11.有一个圆柱,它的高为12 cm,底面半径为3 cm,如图,在圆柱下底面的点A处有一只蚂蚁,它想吃到上底面上与点A相对的点B处的食物,则它沿圆柱侧面爬行的最短路程是________cm.(π取3)
12.如图,若圆锥的高为,高与母线的夹角为30°,则圆锥的侧面积为________.
13.一个正三棱柱的底面边长是3 cm,侧棱长是5 cm,则它的侧面展开图的面积为________cm2.
14.如图是由几个相同的小正方体搭成的立体图形的三视图,则搭成这个立体图形的小正方体的个数是_______________________________________.
15.如图是由若干个大小相同的小正方体堆砌而成的立体图形,那么其三种视图中面积最小的是________.
16.如图是一个用来盛爆米花的圆锥形纸杯,纸杯开口圆的直径EF长为10 cm,母线OE(OF)长为10 cm,在母线OF上的点A处有一块爆米花残渣,且FA=2 cm,一只蚂蚁从杯口的点E处沿圆锥表面爬行到A点,则此蚂蚁爬行的最短路程为________cm.
三、解答题(21题12分,其余每题8分,共44分)
17.画出如图所示的立体图形的三视图.
18.一个圆锥从正面看到的形状为一个边长为2 cm的等边三角形,求其从上面看到的图形的面积.
19.《孙子算经》中有道歌谣算题:“今有竿不知其长,量得影长一丈五尺,立一标杆,长一尺五寸,影长五寸.问竿长几何?”
友情提醒:①歌谣的意思:有一根竹竿不知道有多长,量出它在太阳下的影长为一丈五尺,同时立一根一尺五寸的标杆,它的影长为五寸.请你算一算竹竿的长度是多少.
②丈和尺是古代的长度单位,1丈=10尺,1尺=10寸.
20.蒙古包可以近似地看成是圆锥和圆柱组成的立体图形,如图①所示.
(1)请画出这个立体图形的俯视图;
(2)图②是这个立体图形的正面示意图,已知蒙古包的顶部离地面的高度EO1=6 m,圆柱部分的高OO1=4 m,底面圆的直径BC=8 m,求∠EAO的度数(结果精确到0.1°).
21.学习投影后,小明和小颖利用灯光下自己的影子长度来测量一路灯的高度,并探究影子长度的变化规律.如图,在同一时刻,身高为1.6 m的小明(AB)的影子BC长是3 m,而小颖(EH)刚好在路灯灯泡的正下方H点,并测得HB=6 m.
(1)请在图中画出形成影子的光线,并确定路灯灯泡所在的位置G;
(2)求路灯灯泡的垂直高度GH;
(3)如果小明沿线段BH向小颖(点H)走去,当小明走到BH的中点B1处时,求他的影子B1C1的长;当小明继续走剩下路程的到B2处时,求他的影子B2C2的长;当小明继续走剩下路程的到B3处时……按此规律继续走下去,当小明走剩下路程的到Bn处时,他的影子BnCn的长为多少(直接用含n的代数式表示)?
答案
一、1.C 2.B 3.A
4.B 点拨:根据左视图和主视图可知这个立体图形的底层最少有1+1+1=3(个)小正方体,第二层最少有1个小正方体,因此搭成这个立体图形的小正方体最少有3+1=4(个).
5.B 点拨:圆锥的侧面展开图的弧长==8π,即圆锥的底面圆的周长为8π,∴它的底面圆的半径为=4.
6.A 点拨:连接AC,PO,易知AC经过O点,PO⊥AC.∵∠APC=60°,PA=PC,∴∠PAC=∠PCA=60°.∵四边形ABCD是边长为6 m的正方形,∴AC=6 m,∴OC=3 m,∴PO=OC·tan 60°=3 m.
7.D 点拨:过点G作GQ⊥BE于点Q,GP⊥AB于点P,
易知四边形BQGP是矩形,∴BP=GQ=3米,
∵G是HF的中点,∴HG=1.5米.
由题意知△APG∽△FDE,∴=,∴=,
∴AP=4.875米,∴AB=4.875+3=7.875≈7.9(米).
8.C 点拨:连接BC.由题意可知△ABC是等腰直角三角形,∴BC是⊙O的直径.∴AB=BC×=12 cm,∴扇形ABC的弧长为=6 π(cm),∴圆锥的底面圆的半径是6 π÷2π=3 (cm).
二、9.球体(或正方体)
10.30 11.15 12.2π 13.45 14.5
15.左视图 16.2
三、17.解:如图.
18.解:由题意得圆锥的底面圆的半径为1 cm,∴π×12=π(cm2).
答:该圆锥从上面看到的图形的面积为π cm2.
19.解:竹竿的影长为一丈五尺=15尺,标杆长为一尺五寸=1.5尺,影长为五寸=0.5尺,设竹竿的长度为x尺,
根据题意,得x∶15 =1.5∶0.5 ,解得x=45.
答:竹竿的长度是45尺.
20.解:(1)俯视图如图所示.
(2)∵EO1=6 m,OO1=4 m,
∴EO=EO1-OO1=6-4=2(m),
∵AD=BC=8 m,
∴OA=OD=4 m,
在Rt△AOE中,tan ∠EAO===,则∠EAO≈26.6°.
21.解:(1)如图.
(2)由题意得△ABC∽△GHC.
∴=,即=.∴GH=4.8 m.
(3)如图,由题意可得△A1B1C1∽△GHC1,
∴=.设B1C1长为x m,则=,解得x=,即B1C1= m.
同理=,
∴B2C2=1 m.
∴按此规律可得BnCn= m.
一、选择题(每题3分,共24分)
1.如图是由四个相同的小正方体组成的立体图形,则这个立体图形的左视图是( )
2.如图,某小区内有一条笔直的小路,路的旁边有一盏路灯,晚上小红由A处走到B处.她在灯光照射下的影长l与行走的路程s之间的变化关系,用图象刻画出来,大致图象是( )
3.太阳光垂直照射一扇矩形的窗户,投在平行于窗户的墙上的影子的形状是( )
A.与窗户全等的矩形 B.平行四边形
C.比窗户略小的矩形 D.比窗户略大的矩形
4.由一些大小相同的小正方体搭成的立体图形的主视图和左视图如图,则搭成该立体图形的小正方体的个数最少是( )
A.3 B.4 C.5 D.6
5.若圆锥的母线长是12,侧面展开图的圆心角是120°,则它的底面圆的半径为( )
A.2 B.4 C.6 D.8
6.如图,某剧院舞台上的照明灯P射出的光线成“锥体”,其“锥体”面图的“锥角”是60°.已知舞台ABCD是边长为6 m的正方形,O是“锥体”底面圆的圆心.要使灯光能照射到整个舞台,则灯P的悬挂高度是( )
A.3 m B.3 m C.4 m D. m
7.路边有一根电线杆AB和一块正方形广告牌CDFH,在某一时刻,小明发现在太阳光照射下,电线杆顶端A的影子刚好落在HF的中点G处,而正方形广告牌顶端上的F点的影子刚好落在地面上的E点(如图),已知BC=5米,正方形边长为3米,DE=4米,则电线杆的高度约是( )
A.8米 B.7米 C.6米 D.7.9米
8.如图,从一块直径为24 cm的圆形纸片上剪出一个圆心角为90°的扇形ABC,使点A,B,C在圆周上.将剪下的扇形作为一个圆锥的侧面,则这个圆锥的底面圆的半径是( )
A.12 cm B.6 cm
C.3 cm D.2 cm
二、填空题(每题4分,共32分)
9.若一个几何体的主视图、左视图、俯视图都相同,这个几何体可能是________.(写一个即可)
10.如图,小华为了测量所住楼房的高度,她请来同学帮忙,测量了同一时刻她自己的影长和楼房的影长分别是0.8 m和15 m.已知小华的身高为1.6 m,那么她所住楼房的高度为________m.
11.有一个圆柱,它的高为12 cm,底面半径为3 cm,如图,在圆柱下底面的点A处有一只蚂蚁,它想吃到上底面上与点A相对的点B处的食物,则它沿圆柱侧面爬行的最短路程是________cm.(π取3)
12.如图,若圆锥的高为,高与母线的夹角为30°,则圆锥的侧面积为________.
13.一个正三棱柱的底面边长是3 cm,侧棱长是5 cm,则它的侧面展开图的面积为________cm2.
14.如图是由几个相同的小正方体搭成的立体图形的三视图,则搭成这个立体图形的小正方体的个数是_______________________________________.
15.如图是由若干个大小相同的小正方体堆砌而成的立体图形,那么其三种视图中面积最小的是________.
16.如图是一个用来盛爆米花的圆锥形纸杯,纸杯开口圆的直径EF长为10 cm,母线OE(OF)长为10 cm,在母线OF上的点A处有一块爆米花残渣,且FA=2 cm,一只蚂蚁从杯口的点E处沿圆锥表面爬行到A点,则此蚂蚁爬行的最短路程为________cm.
三、解答题(21题12分,其余每题8分,共44分)
17.画出如图所示的立体图形的三视图.
18.一个圆锥从正面看到的形状为一个边长为2 cm的等边三角形,求其从上面看到的图形的面积.
19.《孙子算经》中有道歌谣算题:“今有竿不知其长,量得影长一丈五尺,立一标杆,长一尺五寸,影长五寸.问竿长几何?”
友情提醒:①歌谣的意思:有一根竹竿不知道有多长,量出它在太阳下的影长为一丈五尺,同时立一根一尺五寸的标杆,它的影长为五寸.请你算一算竹竿的长度是多少.
②丈和尺是古代的长度单位,1丈=10尺,1尺=10寸.
20.蒙古包可以近似地看成是圆锥和圆柱组成的立体图形,如图①所示.
(1)请画出这个立体图形的俯视图;
(2)图②是这个立体图形的正面示意图,已知蒙古包的顶部离地面的高度EO1=6 m,圆柱部分的高OO1=4 m,底面圆的直径BC=8 m,求∠EAO的度数(结果精确到0.1°).
21.学习投影后,小明和小颖利用灯光下自己的影子长度来测量一路灯的高度,并探究影子长度的变化规律.如图,在同一时刻,身高为1.6 m的小明(AB)的影子BC长是3 m,而小颖(EH)刚好在路灯灯泡的正下方H点,并测得HB=6 m.
(1)请在图中画出形成影子的光线,并确定路灯灯泡所在的位置G;
(2)求路灯灯泡的垂直高度GH;
(3)如果小明沿线段BH向小颖(点H)走去,当小明走到BH的中点B1处时,求他的影子B1C1的长;当小明继续走剩下路程的到B2处时,求他的影子B2C2的长;当小明继续走剩下路程的到B3处时……按此规律继续走下去,当小明走剩下路程的到Bn处时,他的影子BnCn的长为多少(直接用含n的代数式表示)?
答案
一、1.C 2.B 3.A
4.B 点拨:根据左视图和主视图可知这个立体图形的底层最少有1+1+1=3(个)小正方体,第二层最少有1个小正方体,因此搭成这个立体图形的小正方体最少有3+1=4(个).
5.B 点拨:圆锥的侧面展开图的弧长==8π,即圆锥的底面圆的周长为8π,∴它的底面圆的半径为=4.
6.A 点拨:连接AC,PO,易知AC经过O点,PO⊥AC.∵∠APC=60°,PA=PC,∴∠PAC=∠PCA=60°.∵四边形ABCD是边长为6 m的正方形,∴AC=6 m,∴OC=3 m,∴PO=OC·tan 60°=3 m.
7.D 点拨:过点G作GQ⊥BE于点Q,GP⊥AB于点P,
易知四边形BQGP是矩形,∴BP=GQ=3米,
∵G是HF的中点,∴HG=1.5米.
由题意知△APG∽△FDE,∴=,∴=,
∴AP=4.875米,∴AB=4.875+3=7.875≈7.9(米).
8.C 点拨:连接BC.由题意可知△ABC是等腰直角三角形,∴BC是⊙O的直径.∴AB=BC×=12 cm,∴扇形ABC的弧长为=6 π(cm),∴圆锥的底面圆的半径是6 π÷2π=3 (cm).
二、9.球体(或正方体)
10.30 11.15 12.2π 13.45 14.5
15.左视图 16.2
三、17.解:如图.
18.解:由题意得圆锥的底面圆的半径为1 cm,∴π×12=π(cm2).
答:该圆锥从上面看到的图形的面积为π cm2.
19.解:竹竿的影长为一丈五尺=15尺,标杆长为一尺五寸=1.5尺,影长为五寸=0.5尺,设竹竿的长度为x尺,
根据题意,得x∶15 =1.5∶0.5 ,解得x=45.
答:竹竿的长度是45尺.
20.解:(1)俯视图如图所示.
(2)∵EO1=6 m,OO1=4 m,
∴EO=EO1-OO1=6-4=2(m),
∵AD=BC=8 m,
∴OA=OD=4 m,
在Rt△AOE中,tan ∠EAO===,则∠EAO≈26.6°.
21.解:(1)如图.
(2)由题意得△ABC∽△GHC.
∴=,即=.∴GH=4.8 m.
(3)如图,由题意可得△A1B1C1∽△GHC1,
∴=.设B1C1长为x m,则=,解得x=,即B1C1= m.
同理=,
∴B2C2=1 m.
∴按此规律可得BnCn= m.
