沪科版 九年级数学下册 第26章 概率初步 单元达标测试卷(word版 含答案)
文档属性
| 名称 | 沪科版 九年级数学下册 第26章 概率初步 单元达标测试卷(word版 含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 152.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-09 19:09:24 | ||
图片预览



文档简介
第26章达标测试卷
一、选择题(每题3分,共30分)
1.下列所给事件中,是必然事件的是( )
A.如果|a|=|b|,那么a=b
B.平分弦的直径垂直于弦,并且平分弦所对的两条弧
C.抛出的篮球会下落
D.五边形的内角和是360°
2.下列事件中,是不可能事件的是( )
A.抛掷2枚正方体骰子,都是6点朝上
B.抛掷2枚硬币,朝上的都是反面
C.从只装有红球的袋子中摸出白球
D.从只装有红、蓝球的袋子中摸出蓝球
3.下列说法中,正确的是( )
A.随机事件发生的概率为1
B.发生概率很小的事件不可能发生
C.不可能事件发生的概率为0
D.抛掷一枚质地均匀的硬币1 000次,正面朝上的次数一定是500
4.某校学生小亮每天骑自行车上学时都要经过一个十字路口,该十字路口有红、黄、绿三色交通信号灯,他在路口遇到红灯的概率为,遇到绿灯的概率为,那么他遇到黄灯的概率为( )
A. B. C. D.
5.5张大小、厚度、颜色相同的卡片上分别画有线段、等边三角形、正方形、正五边形、圆.在看不见图形的条件下任意摸出1张,则这张卡片上的图形是中心对称图形的概率是( )
A. B. C. D.
6.在一个不透明的口袋中装有若干个除颜色不同外其余都相同的球,如果口袋中装有4个红球且摸到红球的概率为,那么口袋中的球共有( )
A.12个 B.9个 C.6个 D.3个
7.如图是两个可以自由转动的转盘,转盘都被等分成三个扇形,分别标上1、2、3和6、7、8这6个数字,如果同时转动这两个转盘各一次(指针落在等分线上重转),转盘停止后,指针指向数字之和为偶数的概率是( )
A. B. C. D.
8.在一个口袋中有4个完全相同的小球.它们的标号分别为1,2,3,4,从中随机摸出一个小球记下标号后放回,再从中随机摸出一个小球,则两次摸出的小球的标号之和大于4的概率为( )
A. B. C. D.
9.在平面直角坐标系中给定以下五个点:A(-2,0)、B(1,0)、C(4,0)、D、E(0,-6),在五个形状、颜色、质量完全相同的乒乓球上标上A、B、C、D、E代表以上五个点.玩摸球游戏,每次摸三个球,摸一次,三球代表的点恰好能确定一条抛物线(对称轴平行于y轴)的概率是( )
A. B. C. D.
10.如图,正方形ABCD的边长为2,将长为2的线段QR的两端放在正方形的相邻的两边上同时滑动.如果点Q从点A出发,沿图中所示方向(A→B→C→D→A)滑动到A停止,同时点R从点B出发,沿图中所示方向(B→C→D→A→B)滑动到B停止,在这个过程中,线段QR的中点M所经过的路线围成的图形的面积记为S.点N是正方形ABCD内任一点,把N点到四个顶点A,B,C,D的距离均不小于1的概率记为P,则S等于( )
A.(4-π)P B.4(1-P) C.4P D.(π-1)P
二、填空题(每题3分,共18分)
11.农科所在相同条件下进行某作物种子发芽率的试验,结果如下表:
种子个数 200 300 500 700 800 900 1 000
发芽种子个数 187 282 435 624 718 814 901
发芽频率 0.935 0.940 0.870 0.891 0.898 0.904 0.901
根据试验所得数据,估计种子发芽的概率是________.(结果保留小数点后一位)
12.如图(1),用八个同样大小的小正方体搭成一个大正方体,小明从上面的四个小正方体(①、②、③、④)中取走任意两个后,得到的新几何体的三视图如图(2)所示的概率为__________.
13.将四张花纹面相同的扑克牌的花纹面都朝上,两张一叠放成两堆不变.若每次可任选一堆的最上面的一张翻看(看后不放回),并全部看完,则共有________种不同的翻牌方式.
14.小明准备买一条毛巾和一条浴巾,此时商店仅剩四条颜色分别是白、黄、蓝、红的毛巾和两条颜色分别为蓝和红的浴巾,如果营业员随机抽取一条毛巾和一条浴巾,那么抽到同一颜色的毛巾和浴巾的概率是____________.
15.如图,△ABC是一块绿化区域,将阴影部分修建为花圃,已知AB=15,AC=9,BC=12,阴影部分是△ABC的内切圆,一只自由飞翔的小鸟将随机落在这块绿化区域上,则小鸟落在花圃上的概率为________.
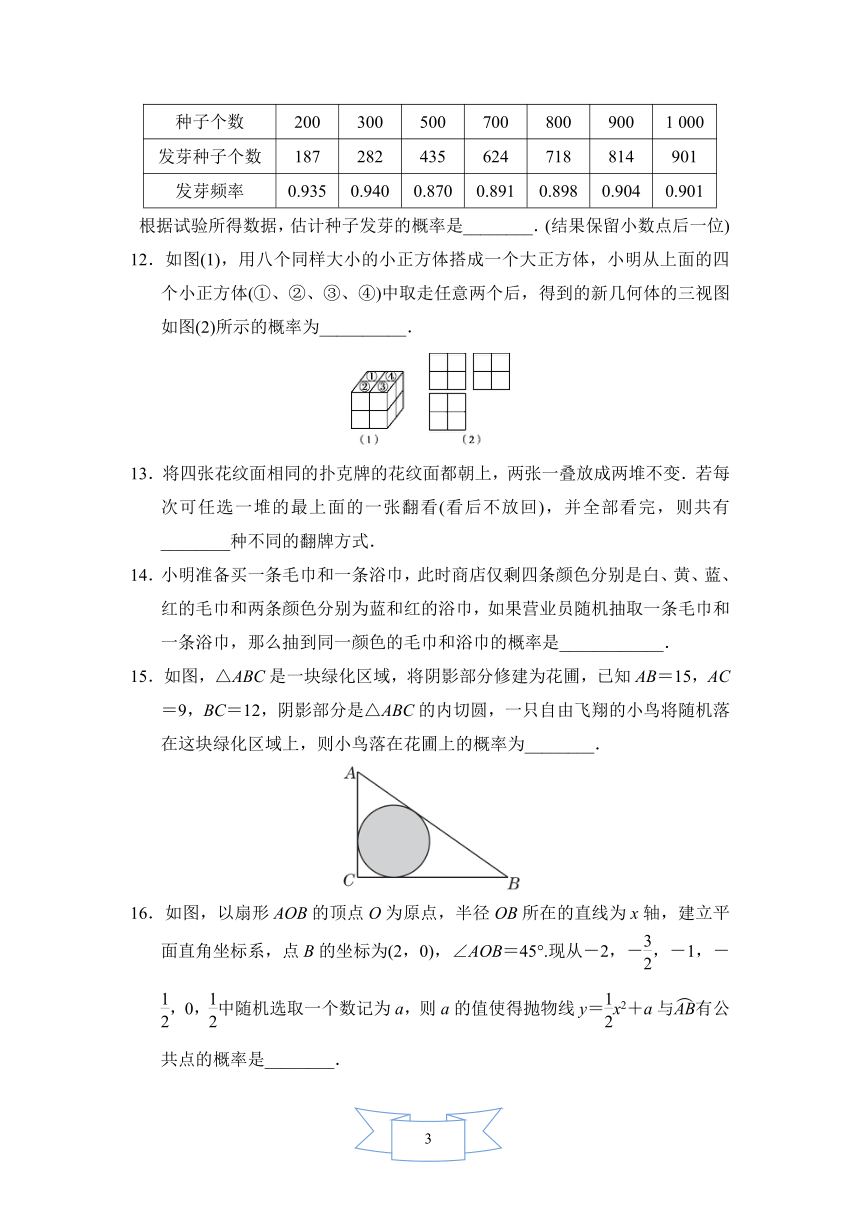
16.如图,以扇形AOB的顶点O为原点,半径OB所在的直线为x轴,建立平面直角坐标系,点B的坐标为(2,0),∠AOB=45°.现从-2,-,-1,-,0,中随机选取一个数记为a,则a的值使得抛物线y=x2+a与有公共点的概率是________.
三、解答题(21,22题每题10分,其余每题8分,共52分)
17.一个不透明的口袋中装有6个红球、9个黄球、3个绿球,这些球除颜色外没有任何区别,从中任意摸出一个球.
(1)求摸到绿球的概率;
(2)再向口袋中放入几个绿球,才能使摸到绿球的概率为?
18.将图中的A型(正方形)、B型(菱形)、C型(等腰直角三角形)纸片分别放在3个盒子中,盒子的形状、大小、质地都相同,再将这3个盒子装入一个不透明的袋子中.
(1)搅匀后从中摸出1个盒子,盒中的纸片既是轴对称图形又是中心对称图形的概率是__________;
(2)搅匀后先从中摸出1个盒子(不放回),再从余下的2个盒子中摸出1个盒子,把摸出的2个盒中的纸片长度相等的边拼在一起,求拼成的图形是轴对称图形的概率.(不重叠无缝隙拼接)
19.一个盒里有标号分别为1,2,3,4,5,6的六个小球,这些小球除标号数字外都相同.
(1)从盒中随机摸出一个小球,求摸到标号数字为奇数的小球的概率;
(2)甲、乙两人用这六个小球玩摸球游戏,规则:甲从盒中随机摸出一个小球,记下标号数字后放回盒中,充分摇匀后,乙再从盒中随机摸出一个小球,并记下标号数字.若两次摸到小球的标号数字同为奇数或同为偶数,则判甲赢;若两次摸到小球的标号数字为一奇一偶,则判乙赢.请用列表法或画树状图法说明这个游戏对甲、乙两人是否公平.
20.有四张正面分别标有数字1,2,3,4的不透明卡片,它们除数字外其余全部相同,现将它们背面朝上洗匀.
(1)随机抽取一张卡片,求抽到数字“2”的概率;
(2)随机抽取一张卡片,然后不放回,再随机抽取一张卡片,请用列表或画树状图的方法求出第一次抽到数字“1”且第二次抽到数字“2”的概率.
21.如图,小晗家客厅装有一种三位单极开关,分别控制着A(楼梯)、B(客厅)、C(走廊)三盏电灯,在正常情况下,小晗按下任意一个开关均可打开对应的一盏电灯,既可三盏、两盏齐开,也可分别单盏开.因刚搬进新房不久,不熟悉情况.
(1)若小晗任意按下一个开关,则正好楼梯灯亮的概率是多少?
(2)若任意按下一个开关后,再按下另两个开关中的一个,则正好客厅灯和走廊灯亮的概率是多少?(请用画树状图法或列表法求解)
22.锐锐参加某市电视台组织的“牡丹杯”智力竞答节目,答对最后两道单选题就顺利通关.第一道单选题有3个选项,第二道单选题有4个选项,这两道题锐锐都不会,不过锐锐还有两个“求助”可以用(使用“求助”一次可以让主持人去掉其中一题的一个错误选项).
(1)如果锐锐两次“求助”都在第一道题中使用,那么锐锐通关的概率是________;
(2)如果锐锐两次“求助”都在第二道题中使用,那么锐锐通关的概率是________;
(3)如果锐锐每道题各用一次“求助”,请用画树状图法或列表法求出他顺利通关的概率.
答案
一、1.C 2.C 3.C
4.D 5.C
6.A 7.C
8.C 点拨:画树状图如图所示.
共有16种等可能的结果,其中两次摸出的小球的标号之和大于4的结果有10种,∴两次摸出的小球的标号之和大于4的概率是=.
9.B
10.C 点拨:连接BM,当Q在A,B之间滑动时,△QBR始终是直角三角形.
∵M为QR的中点,
∴BM=QR=1,
∴M点的运动轨迹是以点B为圆心,1为半径的四分之一圆.
同理,当Q在B,C之间滑动时,M点的运动轨迹是以点C为圆心,1为半径的四分之一圆;
当Q在C,D之间滑动时,M点的运动轨迹是以点D为圆心,1为半径的四分之一圆;当Q在D,A之间滑动时,M点的运动轨迹是以点A为圆心,1为半径的四分之一圆.
∴P=,
∴S=4P.
二、11.0.9 12. 13.6 14. 15. 16.
三、17.解:(1)∵口袋中共有6+9+3=18(个)球,
∴P(摸到绿球)==.
(2)设再向口袋中放入x个绿球,则依题意得=,
解得x=2.经检验,x=2是原方程的解且符合题意.故再向口袋中放入2个绿球,才能使摸到绿球的概率为.
18.解:(1) 点拨:搅匀后从中摸出1个盒子,可能为A型(正方形)、B型(菱形)或C型(等腰直角三角形),共3种等可能结果,其中既是轴对称图形又是中心对称图形的有2种,
∴盒中的纸片既是轴对称图形又是中心对称图形的概率是.
(2)画树状图如下:
共有6种等可能的情况,其中拼成的图形是轴对称图形的情况有2种:A和C,C和A,
∴拼成的图形是轴对称图形的概率为=.
19.解:(1)∵盒里有标号分别为1,2,3,4,5,6的六个小球,标号数字为奇数的小球有三个,
∴摸到标号数字为奇数的小球的概率为=.
(2)画树状图如图.
由树状图可知共有36种等可能的情况,两次摸到小球的标号数字同为奇数或同为偶数的有18种,
两次摸到小球的标号数字为一奇一偶的有18种,
∴P(甲赢)==,P(乙赢)==.
∴P(甲赢)=P(乙赢).
∴这个游戏对甲、乙两人是公平的.
20.解:(1)随机抽取一张卡片,抽到数字“2”的概率为.
(2)画树状图如图.
由树状图可知,共有12种等可能的结果,其中第一次抽到数字“1”且第二次抽到数字“2”的有1种,
故第一次抽到数字“1”且第二次抽到数字“2”的概率为.
21.解:(1)∵小晗家客厅装有一种三位单极开关,分别控制着A(楼梯)、B(客厅)、C(走廊)三盏电灯,
∴小晗任意按下一个开关,正好楼梯灯亮的概率是.
(2)画树状图如图.
∵共有6种等可能的结果,其中正好客厅灯和走廊灯亮的有2种结果,
∴正好客厅灯和走廊灯亮的概率是=.
22.解:(1)
(2)
(3)如果锐锐每道题各用一次“求助”,那么第一道题还有一错一对两个选项,第二道题还有两错一对三个选项.用“对”与“错”分别表示两道题各选项的正误,列表如下:
错 错 对
错 (错,错) (错,错) (错,对)
对 (对,错) (对,错) (对,对)
∵共有6种等可能的结果,其中全部答对的情况有1种,
∴锐锐两道题全部答对的概率为,即他顺利通关的概率是.
一、选择题(每题3分,共30分)
1.下列所给事件中,是必然事件的是( )
A.如果|a|=|b|,那么a=b
B.平分弦的直径垂直于弦,并且平分弦所对的两条弧
C.抛出的篮球会下落
D.五边形的内角和是360°
2.下列事件中,是不可能事件的是( )
A.抛掷2枚正方体骰子,都是6点朝上
B.抛掷2枚硬币,朝上的都是反面
C.从只装有红球的袋子中摸出白球
D.从只装有红、蓝球的袋子中摸出蓝球
3.下列说法中,正确的是( )
A.随机事件发生的概率为1
B.发生概率很小的事件不可能发生
C.不可能事件发生的概率为0
D.抛掷一枚质地均匀的硬币1 000次,正面朝上的次数一定是500
4.某校学生小亮每天骑自行车上学时都要经过一个十字路口,该十字路口有红、黄、绿三色交通信号灯,他在路口遇到红灯的概率为,遇到绿灯的概率为,那么他遇到黄灯的概率为( )
A. B. C. D.
5.5张大小、厚度、颜色相同的卡片上分别画有线段、等边三角形、正方形、正五边形、圆.在看不见图形的条件下任意摸出1张,则这张卡片上的图形是中心对称图形的概率是( )
A. B. C. D.
6.在一个不透明的口袋中装有若干个除颜色不同外其余都相同的球,如果口袋中装有4个红球且摸到红球的概率为,那么口袋中的球共有( )
A.12个 B.9个 C.6个 D.3个
7.如图是两个可以自由转动的转盘,转盘都被等分成三个扇形,分别标上1、2、3和6、7、8这6个数字,如果同时转动这两个转盘各一次(指针落在等分线上重转),转盘停止后,指针指向数字之和为偶数的概率是( )
A. B. C. D.
8.在一个口袋中有4个完全相同的小球.它们的标号分别为1,2,3,4,从中随机摸出一个小球记下标号后放回,再从中随机摸出一个小球,则两次摸出的小球的标号之和大于4的概率为( )
A. B. C. D.
9.在平面直角坐标系中给定以下五个点:A(-2,0)、B(1,0)、C(4,0)、D、E(0,-6),在五个形状、颜色、质量完全相同的乒乓球上标上A、B、C、D、E代表以上五个点.玩摸球游戏,每次摸三个球,摸一次,三球代表的点恰好能确定一条抛物线(对称轴平行于y轴)的概率是( )
A. B. C. D.
10.如图,正方形ABCD的边长为2,将长为2的线段QR的两端放在正方形的相邻的两边上同时滑动.如果点Q从点A出发,沿图中所示方向(A→B→C→D→A)滑动到A停止,同时点R从点B出发,沿图中所示方向(B→C→D→A→B)滑动到B停止,在这个过程中,线段QR的中点M所经过的路线围成的图形的面积记为S.点N是正方形ABCD内任一点,把N点到四个顶点A,B,C,D的距离均不小于1的概率记为P,则S等于( )
A.(4-π)P B.4(1-P) C.4P D.(π-1)P
二、填空题(每题3分,共18分)
11.农科所在相同条件下进行某作物种子发芽率的试验,结果如下表:
种子个数 200 300 500 700 800 900 1 000
发芽种子个数 187 282 435 624 718 814 901
发芽频率 0.935 0.940 0.870 0.891 0.898 0.904 0.901
根据试验所得数据,估计种子发芽的概率是________.(结果保留小数点后一位)
12.如图(1),用八个同样大小的小正方体搭成一个大正方体,小明从上面的四个小正方体(①、②、③、④)中取走任意两个后,得到的新几何体的三视图如图(2)所示的概率为__________.
13.将四张花纹面相同的扑克牌的花纹面都朝上,两张一叠放成两堆不变.若每次可任选一堆的最上面的一张翻看(看后不放回),并全部看完,则共有________种不同的翻牌方式.
14.小明准备买一条毛巾和一条浴巾,此时商店仅剩四条颜色分别是白、黄、蓝、红的毛巾和两条颜色分别为蓝和红的浴巾,如果营业员随机抽取一条毛巾和一条浴巾,那么抽到同一颜色的毛巾和浴巾的概率是____________.
15.如图,△ABC是一块绿化区域,将阴影部分修建为花圃,已知AB=15,AC=9,BC=12,阴影部分是△ABC的内切圆,一只自由飞翔的小鸟将随机落在这块绿化区域上,则小鸟落在花圃上的概率为________.
16.如图,以扇形AOB的顶点O为原点,半径OB所在的直线为x轴,建立平面直角坐标系,点B的坐标为(2,0),∠AOB=45°.现从-2,-,-1,-,0,中随机选取一个数记为a,则a的值使得抛物线y=x2+a与有公共点的概率是________.
三、解答题(21,22题每题10分,其余每题8分,共52分)
17.一个不透明的口袋中装有6个红球、9个黄球、3个绿球,这些球除颜色外没有任何区别,从中任意摸出一个球.
(1)求摸到绿球的概率;
(2)再向口袋中放入几个绿球,才能使摸到绿球的概率为?
18.将图中的A型(正方形)、B型(菱形)、C型(等腰直角三角形)纸片分别放在3个盒子中,盒子的形状、大小、质地都相同,再将这3个盒子装入一个不透明的袋子中.
(1)搅匀后从中摸出1个盒子,盒中的纸片既是轴对称图形又是中心对称图形的概率是__________;
(2)搅匀后先从中摸出1个盒子(不放回),再从余下的2个盒子中摸出1个盒子,把摸出的2个盒中的纸片长度相等的边拼在一起,求拼成的图形是轴对称图形的概率.(不重叠无缝隙拼接)
19.一个盒里有标号分别为1,2,3,4,5,6的六个小球,这些小球除标号数字外都相同.
(1)从盒中随机摸出一个小球,求摸到标号数字为奇数的小球的概率;
(2)甲、乙两人用这六个小球玩摸球游戏,规则:甲从盒中随机摸出一个小球,记下标号数字后放回盒中,充分摇匀后,乙再从盒中随机摸出一个小球,并记下标号数字.若两次摸到小球的标号数字同为奇数或同为偶数,则判甲赢;若两次摸到小球的标号数字为一奇一偶,则判乙赢.请用列表法或画树状图法说明这个游戏对甲、乙两人是否公平.
20.有四张正面分别标有数字1,2,3,4的不透明卡片,它们除数字外其余全部相同,现将它们背面朝上洗匀.
(1)随机抽取一张卡片,求抽到数字“2”的概率;
(2)随机抽取一张卡片,然后不放回,再随机抽取一张卡片,请用列表或画树状图的方法求出第一次抽到数字“1”且第二次抽到数字“2”的概率.
21.如图,小晗家客厅装有一种三位单极开关,分别控制着A(楼梯)、B(客厅)、C(走廊)三盏电灯,在正常情况下,小晗按下任意一个开关均可打开对应的一盏电灯,既可三盏、两盏齐开,也可分别单盏开.因刚搬进新房不久,不熟悉情况.
(1)若小晗任意按下一个开关,则正好楼梯灯亮的概率是多少?
(2)若任意按下一个开关后,再按下另两个开关中的一个,则正好客厅灯和走廊灯亮的概率是多少?(请用画树状图法或列表法求解)
22.锐锐参加某市电视台组织的“牡丹杯”智力竞答节目,答对最后两道单选题就顺利通关.第一道单选题有3个选项,第二道单选题有4个选项,这两道题锐锐都不会,不过锐锐还有两个“求助”可以用(使用“求助”一次可以让主持人去掉其中一题的一个错误选项).
(1)如果锐锐两次“求助”都在第一道题中使用,那么锐锐通关的概率是________;
(2)如果锐锐两次“求助”都在第二道题中使用,那么锐锐通关的概率是________;
(3)如果锐锐每道题各用一次“求助”,请用画树状图法或列表法求出他顺利通关的概率.
答案
一、1.C 2.C 3.C
4.D 5.C
6.A 7.C
8.C 点拨:画树状图如图所示.
共有16种等可能的结果,其中两次摸出的小球的标号之和大于4的结果有10种,∴两次摸出的小球的标号之和大于4的概率是=.
9.B
10.C 点拨:连接BM,当Q在A,B之间滑动时,△QBR始终是直角三角形.
∵M为QR的中点,
∴BM=QR=1,
∴M点的运动轨迹是以点B为圆心,1为半径的四分之一圆.
同理,当Q在B,C之间滑动时,M点的运动轨迹是以点C为圆心,1为半径的四分之一圆;
当Q在C,D之间滑动时,M点的运动轨迹是以点D为圆心,1为半径的四分之一圆;当Q在D,A之间滑动时,M点的运动轨迹是以点A为圆心,1为半径的四分之一圆.
∴P=,
∴S=4P.
二、11.0.9 12. 13.6 14. 15. 16.
三、17.解:(1)∵口袋中共有6+9+3=18(个)球,
∴P(摸到绿球)==.
(2)设再向口袋中放入x个绿球,则依题意得=,
解得x=2.经检验,x=2是原方程的解且符合题意.故再向口袋中放入2个绿球,才能使摸到绿球的概率为.
18.解:(1) 点拨:搅匀后从中摸出1个盒子,可能为A型(正方形)、B型(菱形)或C型(等腰直角三角形),共3种等可能结果,其中既是轴对称图形又是中心对称图形的有2种,
∴盒中的纸片既是轴对称图形又是中心对称图形的概率是.
(2)画树状图如下:
共有6种等可能的情况,其中拼成的图形是轴对称图形的情况有2种:A和C,C和A,
∴拼成的图形是轴对称图形的概率为=.
19.解:(1)∵盒里有标号分别为1,2,3,4,5,6的六个小球,标号数字为奇数的小球有三个,
∴摸到标号数字为奇数的小球的概率为=.
(2)画树状图如图.
由树状图可知共有36种等可能的情况,两次摸到小球的标号数字同为奇数或同为偶数的有18种,
两次摸到小球的标号数字为一奇一偶的有18种,
∴P(甲赢)==,P(乙赢)==.
∴P(甲赢)=P(乙赢).
∴这个游戏对甲、乙两人是公平的.
20.解:(1)随机抽取一张卡片,抽到数字“2”的概率为.
(2)画树状图如图.
由树状图可知,共有12种等可能的结果,其中第一次抽到数字“1”且第二次抽到数字“2”的有1种,
故第一次抽到数字“1”且第二次抽到数字“2”的概率为.
21.解:(1)∵小晗家客厅装有一种三位单极开关,分别控制着A(楼梯)、B(客厅)、C(走廊)三盏电灯,
∴小晗任意按下一个开关,正好楼梯灯亮的概率是.
(2)画树状图如图.
∵共有6种等可能的结果,其中正好客厅灯和走廊灯亮的有2种结果,
∴正好客厅灯和走廊灯亮的概率是=.
22.解:(1)
(2)
(3)如果锐锐每道题各用一次“求助”,那么第一道题还有一错一对两个选项,第二道题还有两错一对三个选项.用“对”与“错”分别表示两道题各选项的正误,列表如下:
错 错 对
错 (错,错) (错,错) (错,对)
对 (对,错) (对,错) (对,对)
∵共有6种等可能的结果,其中全部答对的情况有1种,
∴锐锐两道题全部答对的概率为,即他顺利通关的概率是.
