六年级上册数学导学案 用圆的面积解决实际问题 人教版 无答案
文档属性
| 名称 | 六年级上册数学导学案 用圆的面积解决实际问题 人教版 无答案 |
|
|
| 格式 | doc | ||
| 文件大小 | 36.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-10 00:00:00 | ||
图片预览

文档简介
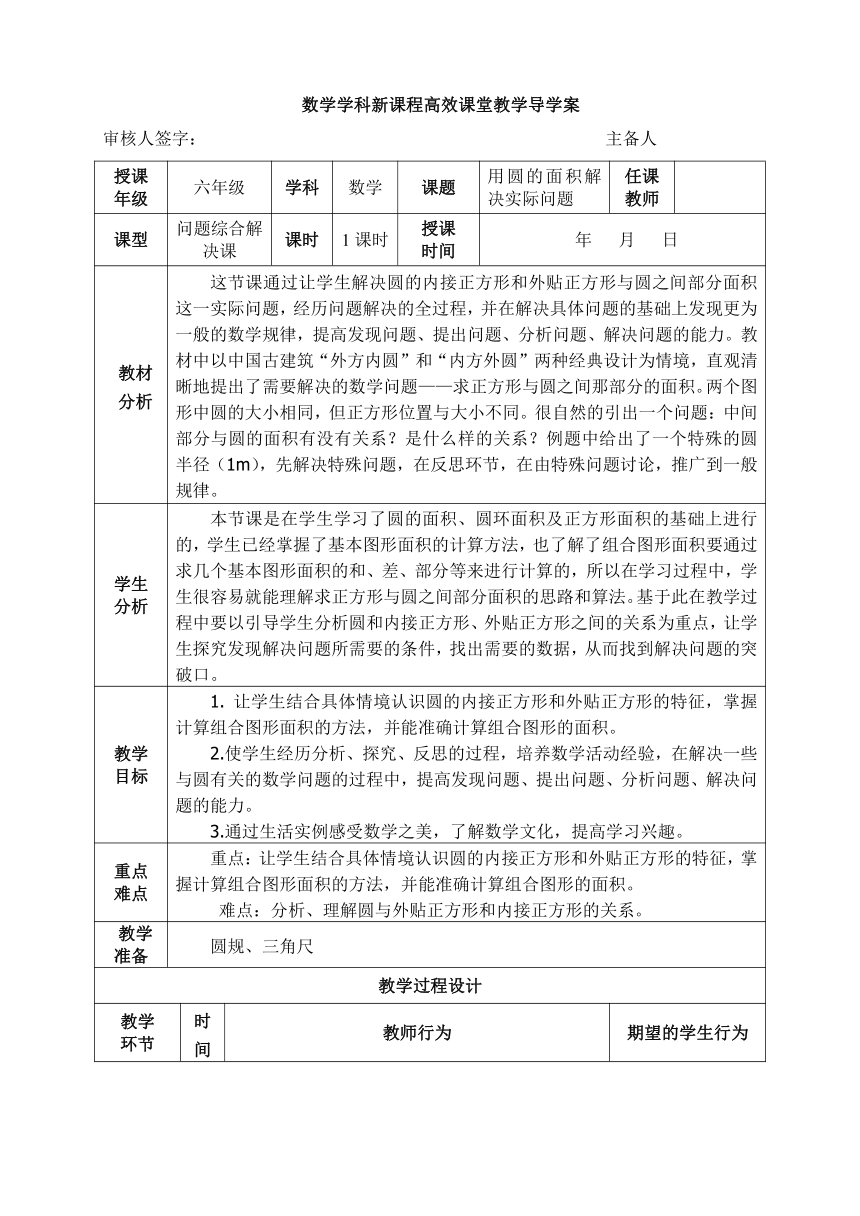
数学学科新课程高效课堂教学导学案
审核人签字: 主备人
授课 年级 六年级 学科 数学 课题 用圆的面积解决实际问题 任课
教师
课型 问题综合解决课 课时 1课时 授课
时间 年 月 日
教材 分析 这节课通过让学生解决圆的内接正方形和外贴正方形与圆之间部分面积这一实际问题,经历问题解决的全过程,并在解决具体问题的基础上发现更为一般的数学规律,提高发现问题、提出问题、分析问题、解决问题的能力。教材中以中国古建筑“外方内圆”和“内方外圆”两种经典设计为情境,直观清晰地提出了需要解决的数学问题——求正方形与圆之间那部分的面积。两个图形中圆的大小相同,但正方形位置与大小不同。很自然的引出一个问题:中间部分与圆的面积有没有关系?是什么样的关系?例题中给出了一个特殊的圆半径(1m),先解决特殊问题,在反思环节,在由特殊问题讨论,推广到一般规律。
学生 分析 本节课是在学生学习了圆的面积、圆环面积及正方形面积的基础上进行的,学生已经掌握了基本图形面积的计算方法,也了解了组合图形面积要通过求几个基本图形面积的和、差、部分等来进行计算的,所以在学习过程中,学生很容易就能理解求正方形与圆之间部分面积的思路和算法。基于此在教学过程中要以引导学生分析圆和内接正方形、外贴正方形之间的关系为重点,让学生探究发现解决问题所需要的条件,找出需要的数据,从而找到解决问题的突破口。
教学 目标 1. 让学生结合具体情境认识圆的内接正方形和外贴正方形的特征,掌握计算组合图形面积的方法,并能准确计算组合图形的面积。
2.使学生经历分析、探究、反思的过程,培养数学活动经验,在解决一些与圆有关的数学问题的过程中,提高发现问题、提出问题、分析问题、解决问题的能力。
3.通过生活实例感受数学之美,了解数学文化,提高学习兴趣。
重点 难点 重点:让学生结合具体情境认识圆的内接正方形和外贴正方形的特征,掌握计算组合图形面积的方法,并能准确计算组合图形的面积。
难点:分析、理解圆与外贴正方形和内接正方形的关系。
教学准备 圆规、三角尺
教学过程设计
教学 环节 时
间 教师行为 期望的学生行为
理解字义,复习方法 5分 1.谈话:同学们听过“组合”这个词吗?你怎样理解它的意思?(板书:组合)
2.提问:我们学过哪些基本的图形?复习基本图形的面积公式。
3.引入新课:今天我们学习与圆有关的组合图形的面积。(板书完整课题) 学生能理解组合图形的意思,在此基础上初步感知组合图形面积的计算方法。复习基本图形的面积计算公式,为后面的学习做好知识准备。
合作学习,探究新知 15分 1.出示例3的两幅图。
(1)提问:同学们在生活中见过这样的图形吗?它们是怎么组成的?
(2)观察这两幅图有什么不同之处。
第一幅:外方内圆;第二幅:外圆内方。
(3)出示课本“阅读与理解”内容。
2.学生小组讨论解答。
(1)小组讨论解决方法。
(2)自己试着解答。
(3)全班交流,派代表出示结果。
左图: 2×4=4(㎡)3.14×1?=3.14(㎡)4-3.14=0.86(㎡)
右图:(×2×1)×2=2(㎡)3.14-2=1.14(㎡)
3.如果两个圆的半径都是r,那结果又是怎样的呢?同桌讨论解决,全班交流结果。
左图: (2r?)-3.14×r?=0.86 r?
右图:3.14×r?-(×2r×r)×2=1.14 r?
4.小结方法。
5.牛刀小试:完成70页做一做和72页第9题。 1.会计算内接正方形、外切正方形与圆之间部分的面积,从特殊到一般,学会此类图形题的解决方法。
2.小组合作学习时要有自己的观点,勇于发表自己的见解。
3.能够独立解答课本70页做一做和72页第9题。
拓展方法,发展思维 15分 1.利用平面图形的学具(正方形、长方形、三角形、圆、半圆等)拼各种组合图形。
2.说一说你拼出的组合图形的面积怎么计算。
3.小结各种不同的方法:
基本图形面积之和;
基本图形面积之差;
基本图形面积的一部分;
基本图形面积之和的一部分;
基本图形面积之差的一部分。
4.利用恰当的方法计算拼出的图形的面积。
5.同桌之间相互交流,指正。 掌握各种组合图形面积的计算方法,能够熟练应用方法解决问题。
梳理知识,总结升华 5分 通过这节课的学习,你有什么收获? 回顾本节课所学的知识,进行归纳小结。
教学 反思
审核人签字: 主备人
授课 年级 六年级 学科 数学 课题 用圆的面积解决实际问题 任课
教师
课型 问题综合解决课 课时 1课时 授课
时间 年 月 日
教材 分析 这节课通过让学生解决圆的内接正方形和外贴正方形与圆之间部分面积这一实际问题,经历问题解决的全过程,并在解决具体问题的基础上发现更为一般的数学规律,提高发现问题、提出问题、分析问题、解决问题的能力。教材中以中国古建筑“外方内圆”和“内方外圆”两种经典设计为情境,直观清晰地提出了需要解决的数学问题——求正方形与圆之间那部分的面积。两个图形中圆的大小相同,但正方形位置与大小不同。很自然的引出一个问题:中间部分与圆的面积有没有关系?是什么样的关系?例题中给出了一个特殊的圆半径(1m),先解决特殊问题,在反思环节,在由特殊问题讨论,推广到一般规律。
学生 分析 本节课是在学生学习了圆的面积、圆环面积及正方形面积的基础上进行的,学生已经掌握了基本图形面积的计算方法,也了解了组合图形面积要通过求几个基本图形面积的和、差、部分等来进行计算的,所以在学习过程中,学生很容易就能理解求正方形与圆之间部分面积的思路和算法。基于此在教学过程中要以引导学生分析圆和内接正方形、外贴正方形之间的关系为重点,让学生探究发现解决问题所需要的条件,找出需要的数据,从而找到解决问题的突破口。
教学 目标 1. 让学生结合具体情境认识圆的内接正方形和外贴正方形的特征,掌握计算组合图形面积的方法,并能准确计算组合图形的面积。
2.使学生经历分析、探究、反思的过程,培养数学活动经验,在解决一些与圆有关的数学问题的过程中,提高发现问题、提出问题、分析问题、解决问题的能力。
3.通过生活实例感受数学之美,了解数学文化,提高学习兴趣。
重点 难点 重点:让学生结合具体情境认识圆的内接正方形和外贴正方形的特征,掌握计算组合图形面积的方法,并能准确计算组合图形的面积。
难点:分析、理解圆与外贴正方形和内接正方形的关系。
教学准备 圆规、三角尺
教学过程设计
教学 环节 时
间 教师行为 期望的学生行为
理解字义,复习方法 5分 1.谈话:同学们听过“组合”这个词吗?你怎样理解它的意思?(板书:组合)
2.提问:我们学过哪些基本的图形?复习基本图形的面积公式。
3.引入新课:今天我们学习与圆有关的组合图形的面积。(板书完整课题) 学生能理解组合图形的意思,在此基础上初步感知组合图形面积的计算方法。复习基本图形的面积计算公式,为后面的学习做好知识准备。
合作学习,探究新知 15分 1.出示例3的两幅图。
(1)提问:同学们在生活中见过这样的图形吗?它们是怎么组成的?
(2)观察这两幅图有什么不同之处。
第一幅:外方内圆;第二幅:外圆内方。
(3)出示课本“阅读与理解”内容。
2.学生小组讨论解答。
(1)小组讨论解决方法。
(2)自己试着解答。
(3)全班交流,派代表出示结果。
左图: 2×4=4(㎡)3.14×1?=3.14(㎡)4-3.14=0.86(㎡)
右图:(×2×1)×2=2(㎡)3.14-2=1.14(㎡)
3.如果两个圆的半径都是r,那结果又是怎样的呢?同桌讨论解决,全班交流结果。
左图: (2r?)-3.14×r?=0.86 r?
右图:3.14×r?-(×2r×r)×2=1.14 r?
4.小结方法。
5.牛刀小试:完成70页做一做和72页第9题。 1.会计算内接正方形、外切正方形与圆之间部分的面积,从特殊到一般,学会此类图形题的解决方法。
2.小组合作学习时要有自己的观点,勇于发表自己的见解。
3.能够独立解答课本70页做一做和72页第9题。
拓展方法,发展思维 15分 1.利用平面图形的学具(正方形、长方形、三角形、圆、半圆等)拼各种组合图形。
2.说一说你拼出的组合图形的面积怎么计算。
3.小结各种不同的方法:
基本图形面积之和;
基本图形面积之差;
基本图形面积的一部分;
基本图形面积之和的一部分;
基本图形面积之差的一部分。
4.利用恰当的方法计算拼出的图形的面积。
5.同桌之间相互交流,指正。 掌握各种组合图形面积的计算方法,能够熟练应用方法解决问题。
梳理知识,总结升华 5分 通过这节课的学习,你有什么收获? 回顾本节课所学的知识,进行归纳小结。
教学 反思
