五年级上册数学课件-5.6 组合图形的面积 沪教版 (共28张PPT)
文档属性
| 名称 | 五年级上册数学课件-5.6 组合图形的面积 沪教版 (共28张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-10 00:00:00 | ||
图片预览

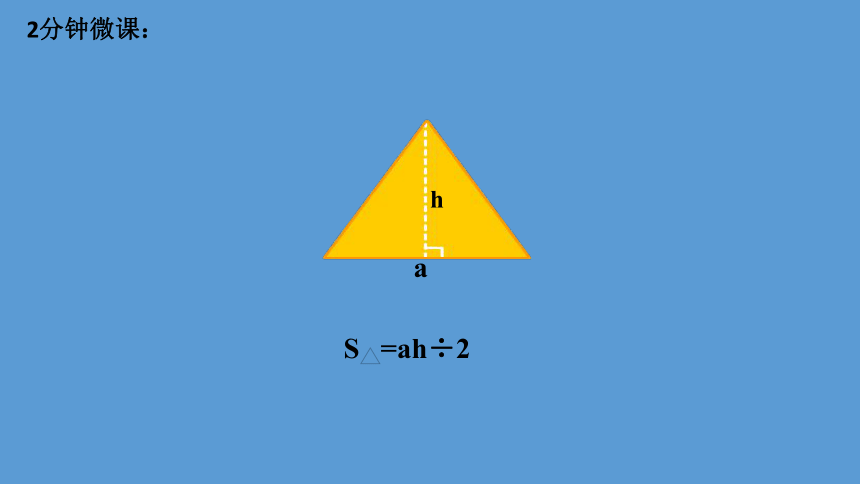
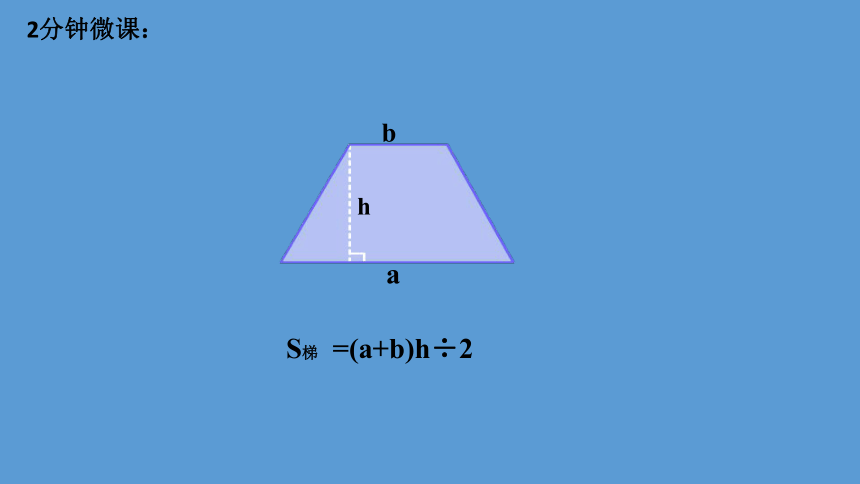

文档简介
组合图形的面积
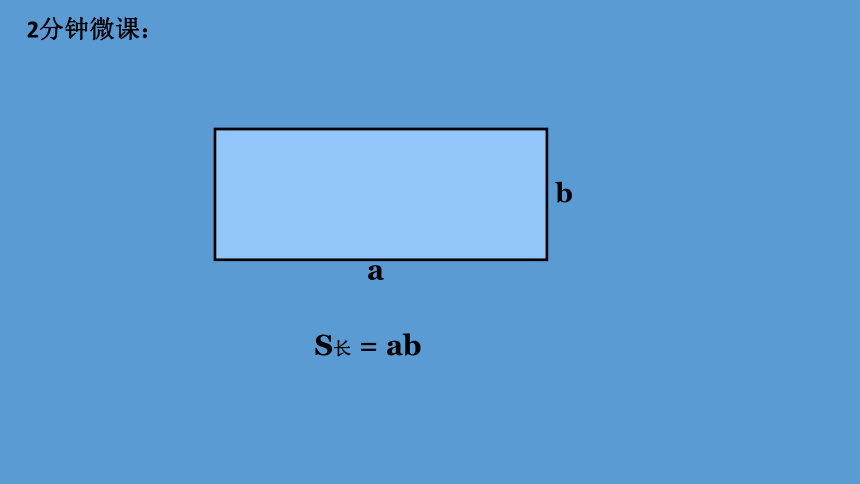
a
b
S长 = ab
2分钟微课:
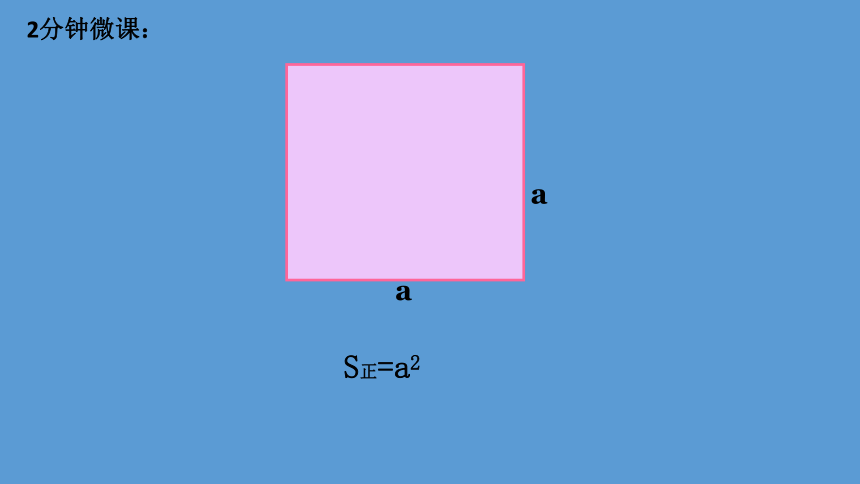
a
a
S正=a2
2分钟微课:
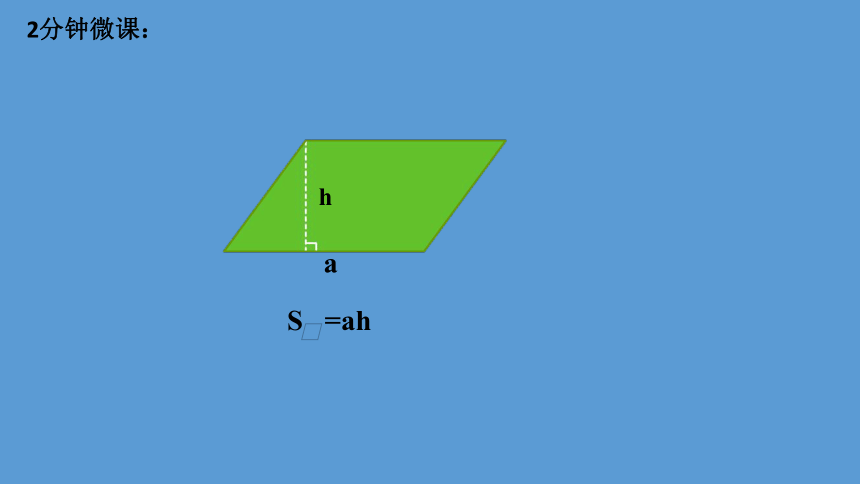
a
h
S =ah
2分钟微课:
a
h
S =ah÷2
2分钟微课:
h
a
b
S梯 =(a+b)h÷2
2分钟微课:
a
b
a
a
a
h
a
h
h
a
b
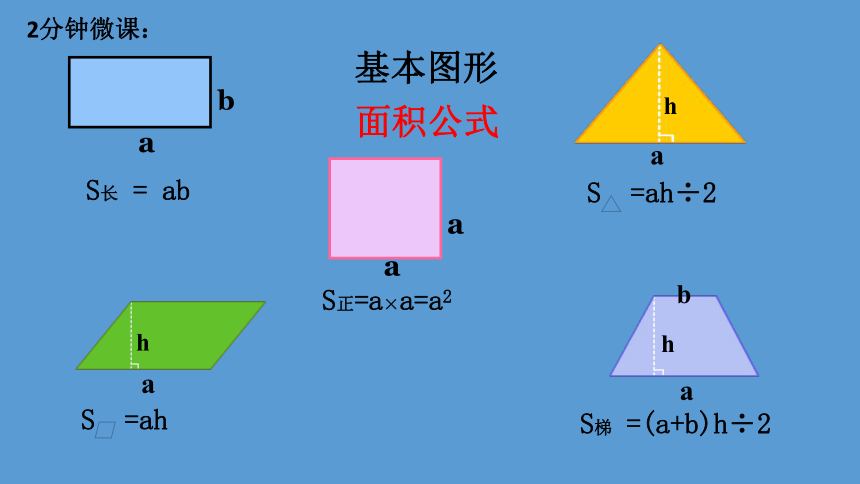
S =ah
S =ah÷2
S梯 =(a+b)h÷2
S正=a×a=a2
S长 = ab
基本图形
面积公式
2分钟微课:
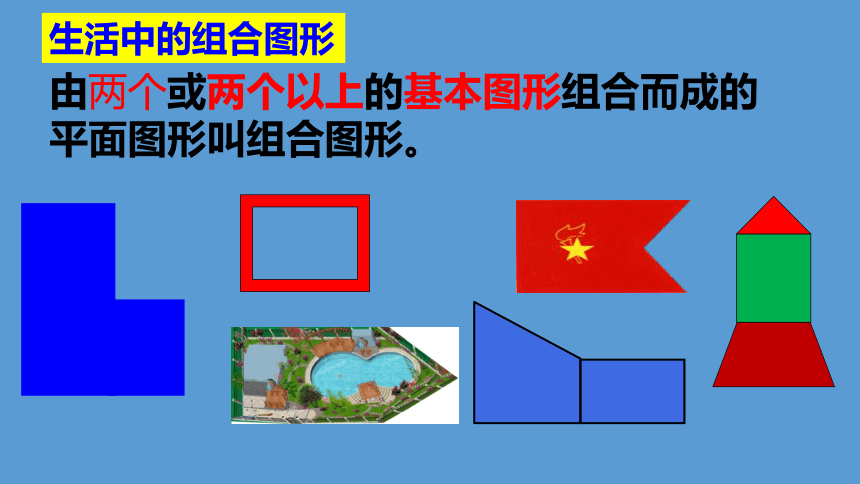
生活中的组合图形
由两个或两个以上的基本图形组合而成的平面图形叫组合图形。
如何求生活中组合图形的面积?
将下面的组合图形转化成你学过的基本图形,你有几种方法?(先独立思考完成再小组交流)
合理转化
添补(求基本图形之差)
分割(求基本图形之和)
转化出的图形越少,计算越简单。
12m
8m
6m
这个花园的面积有多大?
12m
12m
8m
6m
我将它分割成一个长方形和一个三角形:
S1= ab
=12×8
=96(m2)
S1
S2
S2= ah÷2
=8×6÷2
=24(m2)
S组= S1+ S2
=96+24
=120(m2)
解:
答:这个图形的面积是120平方米。
12m
12m
8m
6m
我将它分割成两个相等的梯形:
S1
S2
S1=S2 =(a+b)h÷2
=(12+6+12)×(8÷2)÷2
=30×4÷2
=60(m2)
S组= S1+ S2
=60+60
=120(m2)
解:
答:这个图形的面积是120平方米。
12m
12m
8m
6m
我将它分割成三个三角形:
S1= ab÷2
=8×(12+6)÷2
=72(m2)
S1
S2
S2= S3= ah÷2
=12×(8÷2)÷2
=24(m2)
S组= S1+ S2+S3
=72+24+24
=120(m2)
解:
答:这个图形的面积是120平方米。
12m
S3
12m
8m
6m
我把它拼补成一个长方形:
S1= ab
=(12+6) ×8
=18×8
=144(m2)
S2
S3
S组= S1-S2- S3
=144-12-12
=120(m2)
S2=S3 =ah÷2
=6× (8÷2)÷2
=6×4÷2
=12(m2)
解:
答:这个图形的面积是120平方米。
S1
计算组合图形面积的方法
基本方法
分割求基本图形之和。
添补求基本图形之差。
将组合图形合理分割或添补成已学的基本图形,找准相关数据,利用基本图形面积公式列式计算。
试一试:
数学书P73
10
8
8
4
4
单位:分米
解:
答:这个图形的面积是80平方分米.
脑洞大开
S组=2S =2×40=80(dm2 )
S =ah
= 10 ×(8 ÷2)
= 40 (dm2 )
S组= S长=ab
= 10 ×8
=80(dm2)
下图是由边长分别为6dm和4dm的大小两个正方形组成的,求图中的涂色部分的面积。
脑洞大开
6dm
4dm
4dm
解:S涂=S = ah÷2
=(6+4)×4÷2
=10 ×4 ÷2
=40 ÷2
=20(cm2)
答:涂色部分的面积是20cm2 。
计算组合图形面积的方法
基本方法
分割求基本图形之和。
添补求基本图形之差。
平移成基本图形。
基本方法
将组合图形合理分割、添补、平移、等积变形成已学的基本图形,找准相关数据,利用面积公式列式计算。
计算方法多样化------计算方法择优化
等积变形成基本图形。
√
√
刘徽被称为中国数学史上的牛顿。他利用出入相补原理来计算平面图形的面积。把一个图形经过分割、移补,而面积保持不变,来计算出它的面积。
你知道吗?
《九章算术》
青朱出入图
刘徽
《九章算术》
青出
朱入
朱出
朱方
青方
青入
青入
青出
青出
朱入
朱出
12m
8m
6m
12m
长条
2长
梯
现在求这个花园面积你有没有新的想法?
脑洞大开
12m
8m
6m
我将它平移成一个长方形:
12m
12m
8m
6m
12m
我将它平移成两个长方形:
12m
8m
6m
S2
S3
12m
S1
我运用等积变形将它转化成一个梯形:
今天你有哪些收获?
a
b
S长 = ab
2分钟微课:
a
a
S正=a2
2分钟微课:
a
h
S =ah
2分钟微课:
a
h
S =ah÷2
2分钟微课:
h
a
b
S梯 =(a+b)h÷2
2分钟微课:
a
b
a
a
a
h
a
h
h
a
b
S =ah
S =ah÷2
S梯 =(a+b)h÷2
S正=a×a=a2
S长 = ab
基本图形
面积公式
2分钟微课:
生活中的组合图形
由两个或两个以上的基本图形组合而成的平面图形叫组合图形。
如何求生活中组合图形的面积?
将下面的组合图形转化成你学过的基本图形,你有几种方法?(先独立思考完成再小组交流)
合理转化
添补(求基本图形之差)
分割(求基本图形之和)
转化出的图形越少,计算越简单。
12m
8m
6m
这个花园的面积有多大?
12m
12m
8m
6m
我将它分割成一个长方形和一个三角形:
S1= ab
=12×8
=96(m2)
S1
S2
S2= ah÷2
=8×6÷2
=24(m2)
S组= S1+ S2
=96+24
=120(m2)
解:
答:这个图形的面积是120平方米。
12m
12m
8m
6m
我将它分割成两个相等的梯形:
S1
S2
S1=S2 =(a+b)h÷2
=(12+6+12)×(8÷2)÷2
=30×4÷2
=60(m2)
S组= S1+ S2
=60+60
=120(m2)
解:
答:这个图形的面积是120平方米。
12m
12m
8m
6m
我将它分割成三个三角形:
S1= ab÷2
=8×(12+6)÷2
=72(m2)
S1
S2
S2= S3= ah÷2
=12×(8÷2)÷2
=24(m2)
S组= S1+ S2+S3
=72+24+24
=120(m2)
解:
答:这个图形的面积是120平方米。
12m
S3
12m
8m
6m
我把它拼补成一个长方形:
S1= ab
=(12+6) ×8
=18×8
=144(m2)
S2
S3
S组= S1-S2- S3
=144-12-12
=120(m2)
S2=S3 =ah÷2
=6× (8÷2)÷2
=6×4÷2
=12(m2)
解:
答:这个图形的面积是120平方米。
S1
计算组合图形面积的方法
基本方法
分割求基本图形之和。
添补求基本图形之差。
将组合图形合理分割或添补成已学的基本图形,找准相关数据,利用基本图形面积公式列式计算。
试一试:
数学书P73
10
8
8
4
4
单位:分米
解:
答:这个图形的面积是80平方分米.
脑洞大开
S组=2S =2×40=80(dm2 )
S =ah
= 10 ×(8 ÷2)
= 40 (dm2 )
S组= S长=ab
= 10 ×8
=80(dm2)
下图是由边长分别为6dm和4dm的大小两个正方形组成的,求图中的涂色部分的面积。
脑洞大开
6dm
4dm
4dm
解:S涂=S = ah÷2
=(6+4)×4÷2
=10 ×4 ÷2
=40 ÷2
=20(cm2)
答:涂色部分的面积是20cm2 。
计算组合图形面积的方法
基本方法
分割求基本图形之和。
添补求基本图形之差。
平移成基本图形。
基本方法
将组合图形合理分割、添补、平移、等积变形成已学的基本图形,找准相关数据,利用面积公式列式计算。
计算方法多样化------计算方法择优化
等积变形成基本图形。
√
√
刘徽被称为中国数学史上的牛顿。他利用出入相补原理来计算平面图形的面积。把一个图形经过分割、移补,而面积保持不变,来计算出它的面积。
你知道吗?
《九章算术》
青朱出入图
刘徽
《九章算术》
青出
朱入
朱出
朱方
青方
青入
青入
青出
青出
朱入
朱出
12m
8m
6m
12m
长条
2长
梯
现在求这个花园面积你有没有新的想法?
脑洞大开
12m
8m
6m
我将它平移成一个长方形:
12m
12m
8m
6m
12m
我将它平移成两个长方形:
12m
8m
6m
S2
S3
12m
S1
我运用等积变形将它转化成一个梯形:
今天你有哪些收获?
同课章节目录
