上海市华东师大二附中2021届高三11月周考数学试卷10 PDF版含答案
文档属性
| 名称 | 上海市华东师大二附中2021届高三11月周考数学试卷10 PDF版含答案 |  | |
| 格式 | |||
| 文件大小 | 575.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-10 15:49:08 | ||
图片预览


文档简介
2020-2021 学年上海市 华师大二附中 高 三 11 月 周 考数学试卷 102020.11
一 . 填空题
1. 若 ,且 ,则 ________________.
2.函数 的定义域为 ________________.
3.已知 ,那么 的值是 _____________.
4. 方程 , 实数解 为 _____________.
5.已知 为等差数列,其前 项和为 ,若 , ,则公差 =__________.
6. 是 无穷数列, 已知 是二项式 的展开式各项系数的和,记 ,
则 ____________.
7.已知正方形 ABCD的边长为 1,点 E是 AB边上的动点, 的最大值为 __________.
8.△ 中,三内角 、 、 所对边的长分别为 、 、 , 已知 ,不等式 的
解集为 ,则 ______.
9.从 1,2,3,4,5,6,7,8,9,10这 10个数中任意抽取三个数 ,其中仅有两个数是连续整数的概率是 _____.
10. 为 上的偶函数, 为 上的奇函数且过 , ,则 _____.
11.曲线 C是平面内与两个定点 F1( -1, 0)和 F2( 1, 0)的距离的积等于常数 的点的轨迹 .给出下列三个
结论:① 曲线 C过坐标原点; ② 曲线 C关于坐标原点对称;③若点 P在曲线 C上,则△ F PF 的面积大于 ;
其中,所有正确结论的序号是 _____.
12.设等差数列 满足:公差 , ,且 中任意两项之和也是该数列中的一项 , 若 ,
则 的所有可能取值之和为 _____.
二 . 选择题
13. 设等比数列 的前 项和为 , 则 “ ” 是 “ ” 的()
( A)充分而不必要条件 B)必要而不充分条件 ( C)充要条件 ( D)既不充分又不必要条件
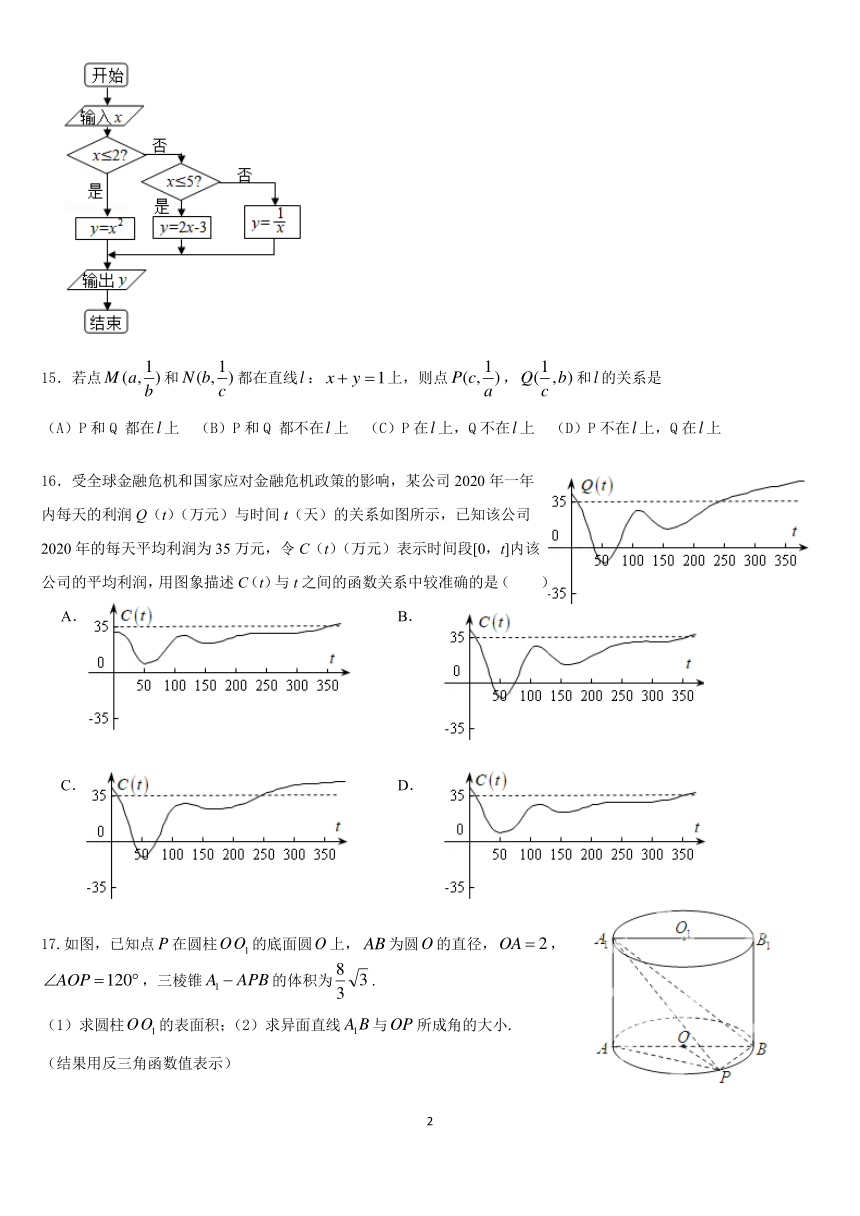
14. 如图给出了一个程序框图,其作用是输入 x值,输出相应的 y值,若要使输入的 x值与输出的 y值相等,
则这样的 x值有( ) A.1个 B.2个 C.3个 D.4个
1
15.若点 和 都在直线 : 上,则点 , 和 的关系是
( A) P和 Q 都在 上 ( B) P和 Q 都不在 上 ( C) P在 上, Q不在 上 ( D) P不在 上, Q在 上
16. 受全球金融危机和国家应对金融危机政策的影响,某公司 2020年一年
内每天的利润 Q(t)(万元)与时间 t(天)的关系如图所示,已知该公司
2020年的每天平均利润为 35万元,令 C(t)(万元)表示时间段 [0,t]内该
公司的平均利润,用图象描述 C(t)与 t之间的函数关系中较准确的是( )
A. B.
C. D.
17.如图,已知点 在圆柱 的底面圆 上, 为圆 的直径, ,
,三棱锥 的体积为 .
( 1)求圆柱 的表面积;( 2)求异面直线 与 所成角的大小 .
(结果用反三角函数值表示)
2
18.某棚户区改造建筑用地平面示意图如图所示.经规划调研确定,棚改规划建筑用地区域近似地为半径是 R的圆
面 ;该圆面的内接四边形 ABCD是原棚户建筑用地,测量可知边界 AB=AD=4万米, BC=6万米, CD=2万米.
(1)请计算原棚户区建筑用地 ABCD的面积及圆面的半径 R的值;
(2)因地理条件的限制,边界 AD、DC不能变更,而边界 AB、BC可以调整,为了提高棚户区改造建筑用地的利用率,
请在圆弧 上设计一点 P;使得棚户区改造的新建筑用地 APCD的面积最大,并求最大值.
19.已知数列 {an}有 a1=a,a2=p(常数 p>0),对任意的正整数 n,Sn=a1+a2+…+an,并有 Sn满足 Sn= .
(1)求 a的值;
(2)试确定数列 {an}是否是等差数列,若是,求出其通项公式,若不是,说明理由;
(3)对于数列 {bn},假如存在一个常数 b使得对任意的正整数 n都有 bn<b,且 bn=b,则称 b为数列 {bn}
的“上渐近值”,令 pn= + ,求数列 {p1+p2+…+pn﹣2n}的“上渐近值”.
20. 已知椭圆 C以 F1(﹣2,0)、F2(2,0)为焦点,且经过点(﹣ , ).(1)求椭圆 C的方程;
(2)已知直线 l过点 P,且直线方向向量为 ( *
3,3),一组直线: l1,l2,…,ln,…,l2n(n∈N )都与直线 l平行,
且与椭圆 C均有交点,它们到直线 l的距离依次为 d,2d,…,nd,…,2nd(d>0),直线 ln恰好过椭圆 C的中心,
试用 n表示 d的关系式,并写出直线 li(i=1,2,…,2n)的方程(用 n,l表示).
(3)在( 2)的条件下,当 i=5时,直线 l5与椭圆 C相交于 A、B两点,若 AB= ,求 n的值.
3
21. 对于数列 A:a1,a2,a3(ai∈N,i=1,2,3),定义“ T变换”: T将数列 A变换成数列 B:b1,b2,b3,其中
bi=|ai﹣ai+1|(i=1,2),且 b3=|a3﹣a1|.这种“ T变换”记作 B=T(A).继续对数列 B进行“ T变换”,得到数列
C:c1,c2,c3,依此类推,当得到的数列各项均为 0时变换结束.
(1)试问 A:2,6,4经过不断的“ T变换”能否结束?若能,请依次写出经过“ T变换”得到的各数列;
若不能,说明理由;
(2)设 A:a1,a2,a3,B=T(A).若 B:b,2,a(a≥b),且 B的各项之和为 2012,求 a,b;
(3)若数列 B再经过 k次“ T变换”得到的数列各项之和最小,求 k的最小值,并说明理由.
4
2020-2021 学年上海市华师大二附中 高三 11 月周考数学试卷 10 参考答案
一 . 填空题
7 1
1. -3-i 2. (0,1] 3. 3 4.
6???? 5. 2 6.
2
7
7. 1 8. 2√3 9.
15 10. -3 11.② 12.364
12. 解:设等差数列的公差为 d,若 5
a1=3 ,=243,则 an=243+(n﹣1)d.
所以数列 {an}中任意两项之和 am+an=243+(m﹣1)d+243+(n﹣1)d=486+(m+n﹣2)d.
设任意一项为 ak=243+(k﹣1)d.则由 am+an=ak可得 243+(m+n﹣k﹣1)d=0,化简可得 d= .
再由 *
k,m,n,d∈N ,可得 k+1﹣m﹣n=1,3,9,27,81,243,
∴d=243,81,27,9,3,1,则 d的所有可能取值之和为 364,故答案为 364.
二 . 选择题 13. C 14. C 15. A 16. D
2
14.解:当 x≤2时, x =x,有 x=0或 x=1;当 2<x≤5时, 2x﹣3=x,有 x=3;
当 x>5时, x= ,x无解.故可知这样的 x值有 3个.故选: C.
16.解: 由已知函数图象可知在起初的几天,每天的平均利润均高于 35,故起初几天的平均利润应高于 35,排除 A,
∵再前 50天内,平均利润为正的天数多于为负的天数,且平均利润为负的函数值的绝对值较小,
∴在 [0,50]内平均利润应不会为负,排除 B、C,故选: D.
三 . 解答题
17. 解:( 1)由题意,在△ AOP中, OA=OP=2,∠AOP=120°,所以 ,
在△ BOP中, OB=OP=2,∠BOP=60°,所以 BP=2,
∴ = ,解得 AA1=4,
故 .
(2)取 AA1中点 Q,连接 OQ,PQ,则 OQ∥A1B,
得∠ POQ或它的补角为异面直线 A1B与 OP所成的角.
又 ,AQ=AO=2,得 ,PQ=4,由余弦定理得 ,
得异面直线 A1B与 OP所成的角为 .
18.解:( 1)因为四边形 ABCD内接于圆,所以∠ ABC+∠ADC=180°,连接 AC,
由余弦定理: 2 2 2
AC =4 +6 ﹣2×4×6×cos∠ABC= 2 2
4 +2 ﹣2×2×4cos∠ADC、
所以 cos∠ABC= ,∵∠ABC∈(0,π),故∠ ABC=60°.
S四边形 ABCD= ×4×6×sin60°+ ×2×4×sin120°=8 (万平方米).
5
在△ 2 2 2
ABC中,由余弦定理: AC =AB +BC ﹣2AB?BC?cos∠ABC=16+36﹣2×4×6× .AC=2 .
由正弦定理 = =2R,∴2R= = = ,∴R= (万米).
(2)∵S四边形 APCD=S△ADC+S△APC,又 S△ADC= AD?CD?sin120°=2 ,
设 AP=x,CP=y.则 S△APC= xy?sin60°= xy.
又由余弦定理 2 2 2 2 2
AC =x +y ﹣2xycos60°=x +y ﹣xy=28.
∴ 2 2
x +y ﹣xy≥2xy﹣xy=xy.∴xy≤28,当且仅当 x=y时取等号
∴S四边形 APCD=2 + xy≤2 + ×28=9 ,∴最大面积为 9 万平方米.
19. 解:( 1)∵Sn= ,∴a1= =0,∴a1=a=0;
(2)由( 1)可知 an=Sn﹣Sn﹣1= ,∴an= an﹣1,
∴an= ? ?…? ? ?a2=(n﹣1)p,∴数列 {an}是以 0为首项、 p为公差的等差数列;
(3)由( 2)可知 Sn= = ,∴pn= + = + =2+2( ﹣ ),
∴p1+p2+…+pn﹣2n=2(1﹣ + ﹣ +…+ ﹣ + ﹣ )
=2(1+ ﹣ ﹣ )=3﹣2( + )<3,
∵ (p1+p2+…+pn﹣2n)=3, ∴数列 {p1+p2+…+pn﹣2n}的“上渐近值”为 3.
20. 解:( 1)∵椭圆 C以 F1(﹣2,0)、F2(2,0)为焦点,且经过点(﹣ , ),
∴ 2
2a=|PF1|+|PF2|=2 ,解得 a= ,∵c=2,∴b =10﹣4=6,∴椭圆 C的方程 .
(2)∵直线 l的方程为 ,整理,得 x﹣y+4=0.
直线 ln∥l且过椭圆的中心,∴直线 ln的方程为 x﹣y=0,由题意知直线 ln到直线 l的距离为 nd,即 ,
∴d= , *
n∈N ,设直线 li(i=1,2,…,2n)的方程为 x﹣y+ci=0,
它们与椭圆 C: 相交,消去 y,得 ,
,解得﹣ 4<ci<4,
6
由题意知:直线 li(i=1,2,…,2n)到 l的距离为 id,∴ ,
∴直线 li(i=1,2,…,2n)的方程为 x﹣y+4(1﹣ )=0.
(3)由题意知 ,由 ,得 ,
设直线 l5与椭圆 C的交点为 A(x1,y1),B(x2,y2),
则 , ,∴ ,解得 n=10,或 n=﹣10(舍),
经检验, n=10.
21. 解: (1)数列 A:2,6,4不能结束,各数列依次为 4,2,2;2,0,2;2,2,0;0,2,2;2,0,2;….
以下重复出现,所以不会出现所有项均为 0的情形.
(2)因为 B的各项之和为 2012,且 a≥b,所以 a为 B的最大项,所以 |a1﹣a3|最大,
即 a1≥a2≥a3,或 a3≥a2≥a1.…(5分)当 a1≥a2≥a3时,可得
由 a+b+2=2012,得 2(a1﹣a3)=2012,即 a=1006,故 b=1004.
当 a3≥a2≥a1时,同理可得 a=1006,b=1004.
(3)方法一: 由 B:b,2,b+2,则 B经过 6次“ T变换”得到的数列分别为: b﹣2,b,2;2,b﹣2,b﹣4;b﹣
4,2,b﹣6;b﹣6,b﹣8,2;2,b﹣10,b﹣8;b﹣12,2,b﹣10.
由此可见,经过 6次“ T变换”后得到的数列也是形如“ b,2,b+2”的数列,与数列 B“结构”完全相同,
但最大项减少 12.因为 1006=12×83+10,所以,数列 B经过 6×83=498次“ T变换”后得到的数列为 8,2,10.
接下来经过“ T 变换”后得到的数列分别为: 6,8,2;2,6,4;4,2,2;2,0,2;2,2,0;0,2,2;2,0,
2,…
从以上分析可知,以后重复出现,所以数列各项和不会更小.
所以经过 498+4=502次“ T变换”得到的数列各项和最小, k的最小值为 502.…(13分)
方法二: 若一个数列有三项,且最小项为 2,较大两项相差 2,则称此数列与数列 B“结构相同”.
若数列 B的三项为 x+2,x,2(x≥2),则无论其顺序如何,经过“ T变换”得到的数列的三项为 x,x﹣2,2
(不考虑顺序).所以与 B结构相同的数列经过“ T变换”得到的数列也与 B结构相同,除 2外其余各项减少 2,
各项和减少 4.
因此,数列 B:1004,2,1006经过 502次“ T变换”一定得到各项为 2,0,2(不考虑顺序)的数列.
通过列举,不难发现各项为 0,2,2的数列,无论顺序如何,经过“ T变换”得到的数列会重复出现,
各项和不再减少.所以,至少通过 502次“ T变换”,得到的数列各项和最小,故 k的最小值为 502.
7
一 . 填空题
1. 若 ,且 ,则 ________________.
2.函数 的定义域为 ________________.
3.已知 ,那么 的值是 _____________.
4. 方程 , 实数解 为 _____________.
5.已知 为等差数列,其前 项和为 ,若 , ,则公差 =__________.
6. 是 无穷数列, 已知 是二项式 的展开式各项系数的和,记 ,
则 ____________.
7.已知正方形 ABCD的边长为 1,点 E是 AB边上的动点, 的最大值为 __________.
8.△ 中,三内角 、 、 所对边的长分别为 、 、 , 已知 ,不等式 的
解集为 ,则 ______.
9.从 1,2,3,4,5,6,7,8,9,10这 10个数中任意抽取三个数 ,其中仅有两个数是连续整数的概率是 _____.
10. 为 上的偶函数, 为 上的奇函数且过 , ,则 _____.
11.曲线 C是平面内与两个定点 F1( -1, 0)和 F2( 1, 0)的距离的积等于常数 的点的轨迹 .给出下列三个
结论:① 曲线 C过坐标原点; ② 曲线 C关于坐标原点对称;③若点 P在曲线 C上,则△ F PF 的面积大于 ;
其中,所有正确结论的序号是 _____.
12.设等差数列 满足:公差 , ,且 中任意两项之和也是该数列中的一项 , 若 ,
则 的所有可能取值之和为 _____.
二 . 选择题
13. 设等比数列 的前 项和为 , 则 “ ” 是 “ ” 的()
( A)充分而不必要条件 B)必要而不充分条件 ( C)充要条件 ( D)既不充分又不必要条件
14. 如图给出了一个程序框图,其作用是输入 x值,输出相应的 y值,若要使输入的 x值与输出的 y值相等,
则这样的 x值有( ) A.1个 B.2个 C.3个 D.4个
1
15.若点 和 都在直线 : 上,则点 , 和 的关系是
( A) P和 Q 都在 上 ( B) P和 Q 都不在 上 ( C) P在 上, Q不在 上 ( D) P不在 上, Q在 上
16. 受全球金融危机和国家应对金融危机政策的影响,某公司 2020年一年
内每天的利润 Q(t)(万元)与时间 t(天)的关系如图所示,已知该公司
2020年的每天平均利润为 35万元,令 C(t)(万元)表示时间段 [0,t]内该
公司的平均利润,用图象描述 C(t)与 t之间的函数关系中较准确的是( )
A. B.
C. D.
17.如图,已知点 在圆柱 的底面圆 上, 为圆 的直径, ,
,三棱锥 的体积为 .
( 1)求圆柱 的表面积;( 2)求异面直线 与 所成角的大小 .
(结果用反三角函数值表示)
2
18.某棚户区改造建筑用地平面示意图如图所示.经规划调研确定,棚改规划建筑用地区域近似地为半径是 R的圆
面 ;该圆面的内接四边形 ABCD是原棚户建筑用地,测量可知边界 AB=AD=4万米, BC=6万米, CD=2万米.
(1)请计算原棚户区建筑用地 ABCD的面积及圆面的半径 R的值;
(2)因地理条件的限制,边界 AD、DC不能变更,而边界 AB、BC可以调整,为了提高棚户区改造建筑用地的利用率,
请在圆弧 上设计一点 P;使得棚户区改造的新建筑用地 APCD的面积最大,并求最大值.
19.已知数列 {an}有 a1=a,a2=p(常数 p>0),对任意的正整数 n,Sn=a1+a2+…+an,并有 Sn满足 Sn= .
(1)求 a的值;
(2)试确定数列 {an}是否是等差数列,若是,求出其通项公式,若不是,说明理由;
(3)对于数列 {bn},假如存在一个常数 b使得对任意的正整数 n都有 bn<b,且 bn=b,则称 b为数列 {bn}
的“上渐近值”,令 pn= + ,求数列 {p1+p2+…+pn﹣2n}的“上渐近值”.
20. 已知椭圆 C以 F1(﹣2,0)、F2(2,0)为焦点,且经过点(﹣ , ).(1)求椭圆 C的方程;
(2)已知直线 l过点 P,且直线方向向量为 ( *
3,3),一组直线: l1,l2,…,ln,…,l2n(n∈N )都与直线 l平行,
且与椭圆 C均有交点,它们到直线 l的距离依次为 d,2d,…,nd,…,2nd(d>0),直线 ln恰好过椭圆 C的中心,
试用 n表示 d的关系式,并写出直线 li(i=1,2,…,2n)的方程(用 n,l表示).
(3)在( 2)的条件下,当 i=5时,直线 l5与椭圆 C相交于 A、B两点,若 AB= ,求 n的值.
3
21. 对于数列 A:a1,a2,a3(ai∈N,i=1,2,3),定义“ T变换”: T将数列 A变换成数列 B:b1,b2,b3,其中
bi=|ai﹣ai+1|(i=1,2),且 b3=|a3﹣a1|.这种“ T变换”记作 B=T(A).继续对数列 B进行“ T变换”,得到数列
C:c1,c2,c3,依此类推,当得到的数列各项均为 0时变换结束.
(1)试问 A:2,6,4经过不断的“ T变换”能否结束?若能,请依次写出经过“ T变换”得到的各数列;
若不能,说明理由;
(2)设 A:a1,a2,a3,B=T(A).若 B:b,2,a(a≥b),且 B的各项之和为 2012,求 a,b;
(3)若数列 B再经过 k次“ T变换”得到的数列各项之和最小,求 k的最小值,并说明理由.
4
2020-2021 学年上海市华师大二附中 高三 11 月周考数学试卷 10 参考答案
一 . 填空题
7 1
1. -3-i 2. (0,1] 3. 3 4.
6???? 5. 2 6.
2
7
7. 1 8. 2√3 9.
15 10. -3 11.② 12.364
12. 解:设等差数列的公差为 d,若 5
a1=3 ,=243,则 an=243+(n﹣1)d.
所以数列 {an}中任意两项之和 am+an=243+(m﹣1)d+243+(n﹣1)d=486+(m+n﹣2)d.
设任意一项为 ak=243+(k﹣1)d.则由 am+an=ak可得 243+(m+n﹣k﹣1)d=0,化简可得 d= .
再由 *
k,m,n,d∈N ,可得 k+1﹣m﹣n=1,3,9,27,81,243,
∴d=243,81,27,9,3,1,则 d的所有可能取值之和为 364,故答案为 364.
二 . 选择题 13. C 14. C 15. A 16. D
2
14.解:当 x≤2时, x =x,有 x=0或 x=1;当 2<x≤5时, 2x﹣3=x,有 x=3;
当 x>5时, x= ,x无解.故可知这样的 x值有 3个.故选: C.
16.解: 由已知函数图象可知在起初的几天,每天的平均利润均高于 35,故起初几天的平均利润应高于 35,排除 A,
∵再前 50天内,平均利润为正的天数多于为负的天数,且平均利润为负的函数值的绝对值较小,
∴在 [0,50]内平均利润应不会为负,排除 B、C,故选: D.
三 . 解答题
17. 解:( 1)由题意,在△ AOP中, OA=OP=2,∠AOP=120°,所以 ,
在△ BOP中, OB=OP=2,∠BOP=60°,所以 BP=2,
∴ = ,解得 AA1=4,
故 .
(2)取 AA1中点 Q,连接 OQ,PQ,则 OQ∥A1B,
得∠ POQ或它的补角为异面直线 A1B与 OP所成的角.
又 ,AQ=AO=2,得 ,PQ=4,由余弦定理得 ,
得异面直线 A1B与 OP所成的角为 .
18.解:( 1)因为四边形 ABCD内接于圆,所以∠ ABC+∠ADC=180°,连接 AC,
由余弦定理: 2 2 2
AC =4 +6 ﹣2×4×6×cos∠ABC= 2 2
4 +2 ﹣2×2×4cos∠ADC、
所以 cos∠ABC= ,∵∠ABC∈(0,π),故∠ ABC=60°.
S四边形 ABCD= ×4×6×sin60°+ ×2×4×sin120°=8 (万平方米).
5
在△ 2 2 2
ABC中,由余弦定理: AC =AB +BC ﹣2AB?BC?cos∠ABC=16+36﹣2×4×6× .AC=2 .
由正弦定理 = =2R,∴2R= = = ,∴R= (万米).
(2)∵S四边形 APCD=S△ADC+S△APC,又 S△ADC= AD?CD?sin120°=2 ,
设 AP=x,CP=y.则 S△APC= xy?sin60°= xy.
又由余弦定理 2 2 2 2 2
AC =x +y ﹣2xycos60°=x +y ﹣xy=28.
∴ 2 2
x +y ﹣xy≥2xy﹣xy=xy.∴xy≤28,当且仅当 x=y时取等号
∴S四边形 APCD=2 + xy≤2 + ×28=9 ,∴最大面积为 9 万平方米.
19. 解:( 1)∵Sn= ,∴a1= =0,∴a1=a=0;
(2)由( 1)可知 an=Sn﹣Sn﹣1= ,∴an= an﹣1,
∴an= ? ?…? ? ?a2=(n﹣1)p,∴数列 {an}是以 0为首项、 p为公差的等差数列;
(3)由( 2)可知 Sn= = ,∴pn= + = + =2+2( ﹣ ),
∴p1+p2+…+pn﹣2n=2(1﹣ + ﹣ +…+ ﹣ + ﹣ )
=2(1+ ﹣ ﹣ )=3﹣2( + )<3,
∵ (p1+p2+…+pn﹣2n)=3, ∴数列 {p1+p2+…+pn﹣2n}的“上渐近值”为 3.
20. 解:( 1)∵椭圆 C以 F1(﹣2,0)、F2(2,0)为焦点,且经过点(﹣ , ),
∴ 2
2a=|PF1|+|PF2|=2 ,解得 a= ,∵c=2,∴b =10﹣4=6,∴椭圆 C的方程 .
(2)∵直线 l的方程为 ,整理,得 x﹣y+4=0.
直线 ln∥l且过椭圆的中心,∴直线 ln的方程为 x﹣y=0,由题意知直线 ln到直线 l的距离为 nd,即 ,
∴d= , *
n∈N ,设直线 li(i=1,2,…,2n)的方程为 x﹣y+ci=0,
它们与椭圆 C: 相交,消去 y,得 ,
,解得﹣ 4<ci<4,
6
由题意知:直线 li(i=1,2,…,2n)到 l的距离为 id,∴ ,
∴直线 li(i=1,2,…,2n)的方程为 x﹣y+4(1﹣ )=0.
(3)由题意知 ,由 ,得 ,
设直线 l5与椭圆 C的交点为 A(x1,y1),B(x2,y2),
则 , ,∴ ,解得 n=10,或 n=﹣10(舍),
经检验, n=10.
21. 解: (1)数列 A:2,6,4不能结束,各数列依次为 4,2,2;2,0,2;2,2,0;0,2,2;2,0,2;….
以下重复出现,所以不会出现所有项均为 0的情形.
(2)因为 B的各项之和为 2012,且 a≥b,所以 a为 B的最大项,所以 |a1﹣a3|最大,
即 a1≥a2≥a3,或 a3≥a2≥a1.…(5分)当 a1≥a2≥a3时,可得
由 a+b+2=2012,得 2(a1﹣a3)=2012,即 a=1006,故 b=1004.
当 a3≥a2≥a1时,同理可得 a=1006,b=1004.
(3)方法一: 由 B:b,2,b+2,则 B经过 6次“ T变换”得到的数列分别为: b﹣2,b,2;2,b﹣2,b﹣4;b﹣
4,2,b﹣6;b﹣6,b﹣8,2;2,b﹣10,b﹣8;b﹣12,2,b﹣10.
由此可见,经过 6次“ T变换”后得到的数列也是形如“ b,2,b+2”的数列,与数列 B“结构”完全相同,
但最大项减少 12.因为 1006=12×83+10,所以,数列 B经过 6×83=498次“ T变换”后得到的数列为 8,2,10.
接下来经过“ T 变换”后得到的数列分别为: 6,8,2;2,6,4;4,2,2;2,0,2;2,2,0;0,2,2;2,0,
2,…
从以上分析可知,以后重复出现,所以数列各项和不会更小.
所以经过 498+4=502次“ T变换”得到的数列各项和最小, k的最小值为 502.…(13分)
方法二: 若一个数列有三项,且最小项为 2,较大两项相差 2,则称此数列与数列 B“结构相同”.
若数列 B的三项为 x+2,x,2(x≥2),则无论其顺序如何,经过“ T变换”得到的数列的三项为 x,x﹣2,2
(不考虑顺序).所以与 B结构相同的数列经过“ T变换”得到的数列也与 B结构相同,除 2外其余各项减少 2,
各项和减少 4.
因此,数列 B:1004,2,1006经过 502次“ T变换”一定得到各项为 2,0,2(不考虑顺序)的数列.
通过列举,不难发现各项为 0,2,2的数列,无论顺序如何,经过“ T变换”得到的数列会重复出现,
各项和不再减少.所以,至少通过 502次“ T变换”,得到的数列各项和最小,故 k的最小值为 502.
7
同课章节目录
