11.24三角形全等的条件4直角三角形
文档属性
| 名称 | 11.24三角形全等的条件4直角三角形 |  | |
| 格式 | rar | ||
| 文件大小 | 145.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-10-21 09:19:09 | ||
图片预览


文档简介
(共10张PPT)
§11.2.4 三角形全等的条件
想一想:
1:如图:(1) △ABC≌△DEF,指出它们的对应 顶点、对应角、对应边。
A
D
B
E
C
F
2:我们已经学过判定全等三角形的方法有哪些?
AB——DE
AC——DF
BC——EF
∠A——∠D
∠B——∠DEF
∠ACB——∠F
(SSS)、(SAS)、(ASA)、(AAS)
思考:
1:如图:Rt△ACB、与Rt△A1C1B1中,∠C与∠C1是直角,用我们已经学过的知识,除了两直角相等以外,你还能补充哪些条件就能使这两个直角三角形全等?
A
B
C
A1
B1
C1
2: 如果两个直角三角形满足斜边和一条直角边对应相等,这两个直角三角形全等吗?
画一画:
画一个Rt△ACB ,使∠C﹦90°,AB=4cm,AC=3cm.
(1):你能试着画出来吗?
(2):把画好的Rt△ACB与同桌交流一下,能否完全重合
(3):你能写出画法吗
规律:
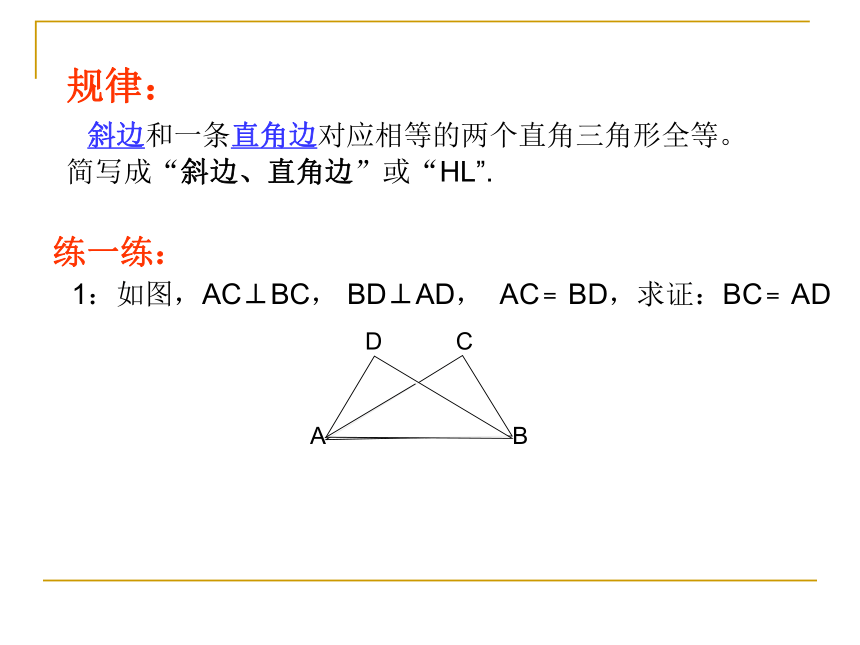
斜边和一条直角边对应相等的两个直角三角形全等。
简写成“斜边、直角边”或“HL”.
练一练:
1:如图,AC⊥BC, BD⊥AD, AC﹦BD,求证:BC﹦AD
A
B
C
D
A
F
C
E
D
B
如图,AB=CD, BF⊥AC,DE⊥AC,AE=CF
求证:BF=DE
变式1:
BD平分EF吗?
G
A
F
C
E
D
B
如图,AB=CD, BF⊥AC,DE⊥AC,AE=CF
想一想:BD平分EF吗
G
变式2:
议一议
如图,有两个长度相同的滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,两个滑梯的倾斜角∠ABC和∠DFE的大小有什么关系?
∠ABC+∠DFE=90°
实际应用
解:在Rt△ABC和Rt△DEF中
BC=EF,
AC=DF .
∴ Rt△ABC≌Rt△DEF (HL).
∴∠ABC=∠DEF
(全等三角形对应角相等).
∵ ∠DEF+∠DFE=90°,
∴∠ABC+∠DFE=90°.
§11.2.4 三角形全等的条件
想一想:
1:如图:(1) △ABC≌△DEF,指出它们的对应 顶点、对应角、对应边。
A
D
B
E
C
F
2:我们已经学过判定全等三角形的方法有哪些?
AB——DE
AC——DF
BC——EF
∠A——∠D
∠B——∠DEF
∠ACB——∠F
(SSS)、(SAS)、(ASA)、(AAS)
思考:
1:如图:Rt△ACB、与Rt△A1C1B1中,∠C与∠C1是直角,用我们已经学过的知识,除了两直角相等以外,你还能补充哪些条件就能使这两个直角三角形全等?
A
B
C
A1
B1
C1
2: 如果两个直角三角形满足斜边和一条直角边对应相等,这两个直角三角形全等吗?
画一画:
画一个Rt△ACB ,使∠C﹦90°,AB=4cm,AC=3cm.
(1):你能试着画出来吗?
(2):把画好的Rt△ACB与同桌交流一下,能否完全重合
(3):你能写出画法吗
规律:
斜边和一条直角边对应相等的两个直角三角形全等。
简写成“斜边、直角边”或“HL”.
练一练:
1:如图,AC⊥BC, BD⊥AD, AC﹦BD,求证:BC﹦AD
A
B
C
D
A
F
C
E
D
B
如图,AB=CD, BF⊥AC,DE⊥AC,AE=CF
求证:BF=DE
变式1:
BD平分EF吗?
G
A
F
C
E
D
B
如图,AB=CD, BF⊥AC,DE⊥AC,AE=CF
想一想:BD平分EF吗
G
变式2:
议一议
如图,有两个长度相同的滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,两个滑梯的倾斜角∠ABC和∠DFE的大小有什么关系?
∠ABC+∠DFE=90°
实际应用
解:在Rt△ABC和Rt△DEF中
BC=EF,
AC=DF .
∴ Rt△ABC≌Rt△DEF (HL).
∴∠ABC=∠DEF
(全等三角形对应角相等).
∵ ∠DEF+∠DFE=90°,
∴∠ABC+∠DFE=90°.
