11.2三角形全等判定3
文档属性
| 名称 | 11.2三角形全等判定3 |  | |
| 格式 | rar | ||
| 文件大小 | 268.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-10-21 09:19:09 | ||
图片预览




文档简介
(共12张PPT)
全等三角形的判定(三)
执教者:王 平
全等三角形的判定(三)
——角边角公理
目的要求
复习引入
探究新知
巩固练习
布置作业
目的要求:
1、使学生理解判定两三角形全等的角边角公理,并能运用这个方法证明线段或角的相等。
2、通过画图发现规律,并用之解决问题。
重点难点:
1、重点 : 熟悉判定两三角形全等的角边角公理。
2、难点:通过两个三角形全等,间接证明线段或角相等及两线平行、垂直等。
复习:
2、记得“边边边”、“边角边”的具体内容吗?
3、当两边及其中一边的对角对应相等的两个三角形一定全等吗?
三边对应相等的两个三角形全等;
两边和它们的夹角对应相等的两个三角形全等。
不一定全等
1、前面我们学习过哪几种判定两个三角形全等的方法?
边边边;边角边
A
C
B
A′
C′
B′
D
E
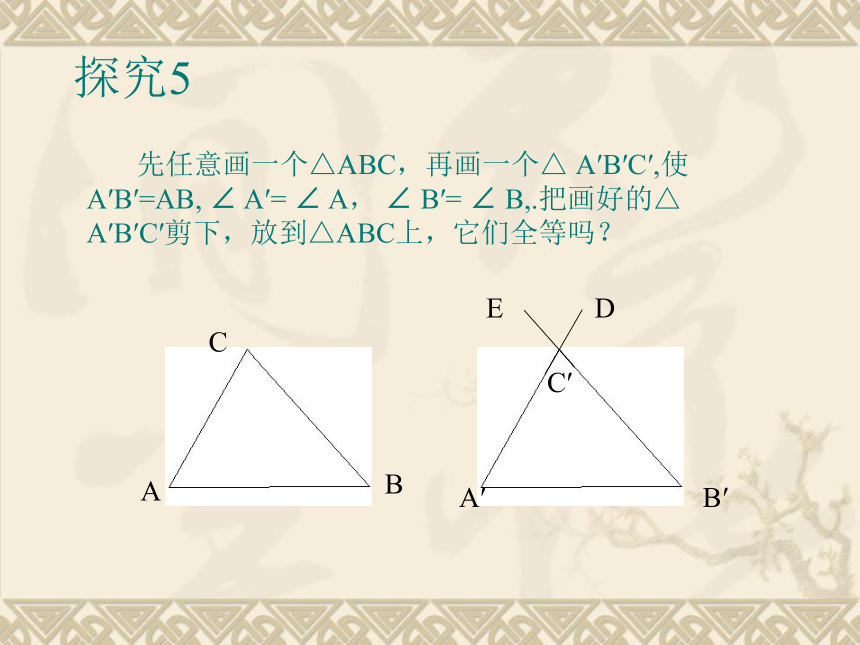
先任意画一个△ABC,再画一个△ A′B′C′,使A′B′=AB, ∠ A′= ∠ A, ∠ B′= ∠ B,.把画好的△ A′B′C′剪下,放到△ABC上,它们全等吗?
探究5
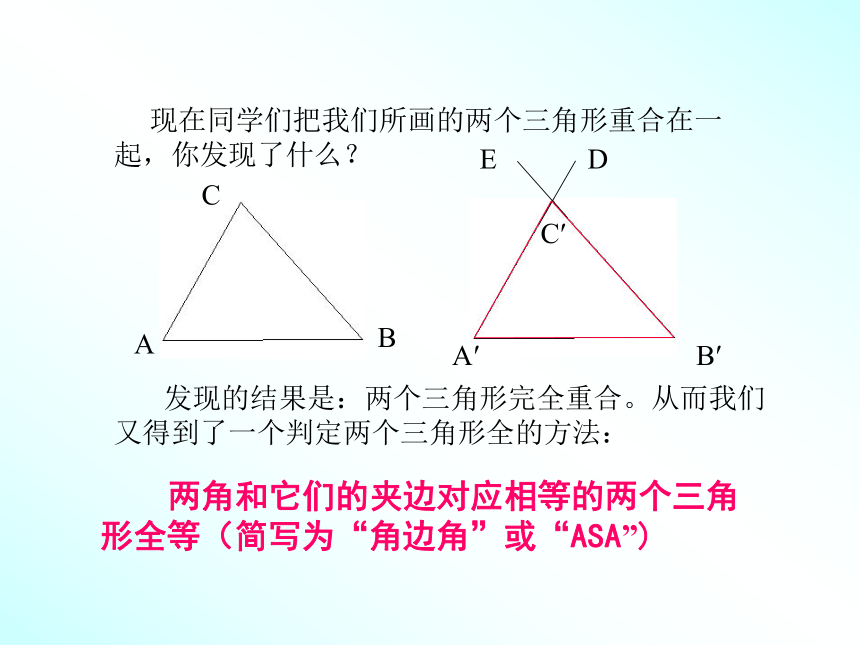
现在同学们把我们所画的两个三角形重合在一起,你发现了什么?
两角和它们的夹边对应相等的两个三角形全等(简写为“角边角”或“ASA”)
发现的结果是:两个三角形完全重合。从而我们又得到了一个判定两个三角形全的方法:
A
C
B
A′
C′
B′
D
E
证明:
在△ACB和△ADB中
∠DAB=∠CAB
AB=AB (公共边)
∠ABD=∠ABC
∴ △ACB≌△ADB (ASA)
∴AC=AD
A
D
B
C
例1、 已知:如图,∠DBA=∠CBA,
∠DAB=∠CAB
求证:AC=AD
从上面可知:两个角和其中一个角的对边对应相等的两个三角形全等。简写成“角角边”或“AAS”
探究6
A
B
C
D
E
F
在△ ABC和△ DEF中, ∠ A= ∠ D, ∠ B= ∠ E,BC=EF, △ABC与△DEF全等吗?能利用角边角证明你的结论吗?
在△ABC和△DEF中
∠C=∠F
AB=EF
∠B=∠E
∴ △ABC≌△DEF (ASA)
证明:
∵ ∠ A= ∠ D, ∠ B= ∠ E
∴ 1800-∠ A -∠ B =1800-∠ D- ∠ E
即∠ C= ∠ F
证明:在△ABE和△ACD中
∠A= ∠A(公共角)
AB=AC
∠B=∠C
∴ △ABE≌△ACD (ASA)
∴ AD=AE
∵ AB=AC
∴ AB-AD=AC-AE
例2、已知:点D在AB上,点E在AC,AB=AC,
∠B=∠C.
求证:BD=CE
即 BD=CE
巩固练习:
一、判断题:
1、有两角和一边对应相等的两个三角形全等。( )
2、有两边和一角对应相等的两个三角形全等。( )
二、填空题:
1、如图1,AD交BC于O,AB∥CD且AB=CD,那么AO= , BO= ,
2、若△ABC的∠B=∠C, △ A′B′C′的∠ B′=∠ C′,且BC= B′C′,那么△ABC与△ A′B′C′全等吗? 。
3、如图2,AC=AB,AD平分CAD,E在AD上,则图
中全等的三角形有 对,说一说分别是哪些,为什么?
(图1 )
A
B
D
C
O
A
B
D
C
E
(图2 )
√
×
DO
CO
不一定全等
三
二、课外作业:
1、已知,如图1:∠ABE=∠CBD, ∠BCE=∠DBA,EC=AD
求证:AB=BE,BC=DB
2、已知,如图2:AD, EF,BC交于O,且AO=OD,BO=OC,EO=OF
求证:△AEB≌△DFC
(图1 )
(图2 )
一、书本作业
P15:5、6、10题,练习册第3课时
全等三角形的判定(三)
执教者:王 平
全等三角形的判定(三)
——角边角公理
目的要求
复习引入
探究新知
巩固练习
布置作业
目的要求:
1、使学生理解判定两三角形全等的角边角公理,并能运用这个方法证明线段或角的相等。
2、通过画图发现规律,并用之解决问题。
重点难点:
1、重点 : 熟悉判定两三角形全等的角边角公理。
2、难点:通过两个三角形全等,间接证明线段或角相等及两线平行、垂直等。
复习:
2、记得“边边边”、“边角边”的具体内容吗?
3、当两边及其中一边的对角对应相等的两个三角形一定全等吗?
三边对应相等的两个三角形全等;
两边和它们的夹角对应相等的两个三角形全等。
不一定全等
1、前面我们学习过哪几种判定两个三角形全等的方法?
边边边;边角边
A
C
B
A′
C′
B′
D
E
先任意画一个△ABC,再画一个△ A′B′C′,使A′B′=AB, ∠ A′= ∠ A, ∠ B′= ∠ B,.把画好的△ A′B′C′剪下,放到△ABC上,它们全等吗?
探究5
现在同学们把我们所画的两个三角形重合在一起,你发现了什么?
两角和它们的夹边对应相等的两个三角形全等(简写为“角边角”或“ASA”)
发现的结果是:两个三角形完全重合。从而我们又得到了一个判定两个三角形全的方法:
A
C
B
A′
C′
B′
D
E
证明:
在△ACB和△ADB中
∠DAB=∠CAB
AB=AB (公共边)
∠ABD=∠ABC
∴ △ACB≌△ADB (ASA)
∴AC=AD
A
D
B
C
例1、 已知:如图,∠DBA=∠CBA,
∠DAB=∠CAB
求证:AC=AD
从上面可知:两个角和其中一个角的对边对应相等的两个三角形全等。简写成“角角边”或“AAS”
探究6
A
B
C
D
E
F
在△ ABC和△ DEF中, ∠ A= ∠ D, ∠ B= ∠ E,BC=EF, △ABC与△DEF全等吗?能利用角边角证明你的结论吗?
在△ABC和△DEF中
∠C=∠F
AB=EF
∠B=∠E
∴ △ABC≌△DEF (ASA)
证明:
∵ ∠ A= ∠ D, ∠ B= ∠ E
∴ 1800-∠ A -∠ B =1800-∠ D- ∠ E
即∠ C= ∠ F
证明:在△ABE和△ACD中
∠A= ∠A(公共角)
AB=AC
∠B=∠C
∴ △ABE≌△ACD (ASA)
∴ AD=AE
∵ AB=AC
∴ AB-AD=AC-AE
例2、已知:点D在AB上,点E在AC,AB=AC,
∠B=∠C.
求证:BD=CE
即 BD=CE
巩固练习:
一、判断题:
1、有两角和一边对应相等的两个三角形全等。( )
2、有两边和一角对应相等的两个三角形全等。( )
二、填空题:
1、如图1,AD交BC于O,AB∥CD且AB=CD,那么AO= , BO= ,
2、若△ABC的∠B=∠C, △ A′B′C′的∠ B′=∠ C′,且BC= B′C′,那么△ABC与△ A′B′C′全等吗? 。
3、如图2,AC=AB,AD平分CAD,E在AD上,则图
中全等的三角形有 对,说一说分别是哪些,为什么?
(图1 )
A
B
D
C
O
A
B
D
C
E
(图2 )
√
×
DO
CO
不一定全等
三
二、课外作业:
1、已知,如图1:∠ABE=∠CBD, ∠BCE=∠DBA,EC=AD
求证:AB=BE,BC=DB
2、已知,如图2:AD, EF,BC交于O,且AO=OD,BO=OC,EO=OF
求证:△AEB≌△DFC
(图1 )
(图2 )
一、书本作业
P15:5、6、10题,练习册第3课时
