第二十四章 圆 复习课件(共34张PPT)-2020-2021学年九年级数学下册单元复习一遍过(沪科版)
文档属性
| 名称 | 第二十四章 圆 复习课件(共34张PPT)-2020-2021学年九年级数学下册单元复习一遍过(沪科版) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-12 00:00:00 | ||
图片预览









文档简介
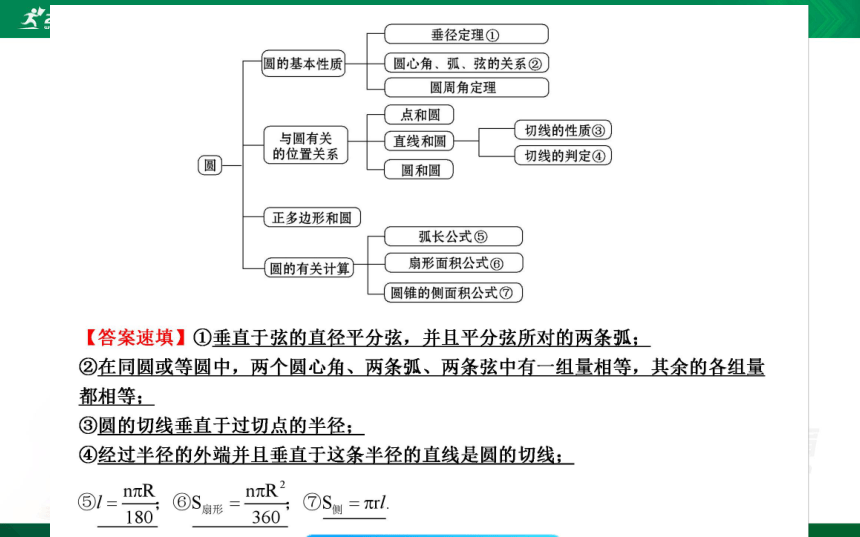
第二十四章 圆
复习课件
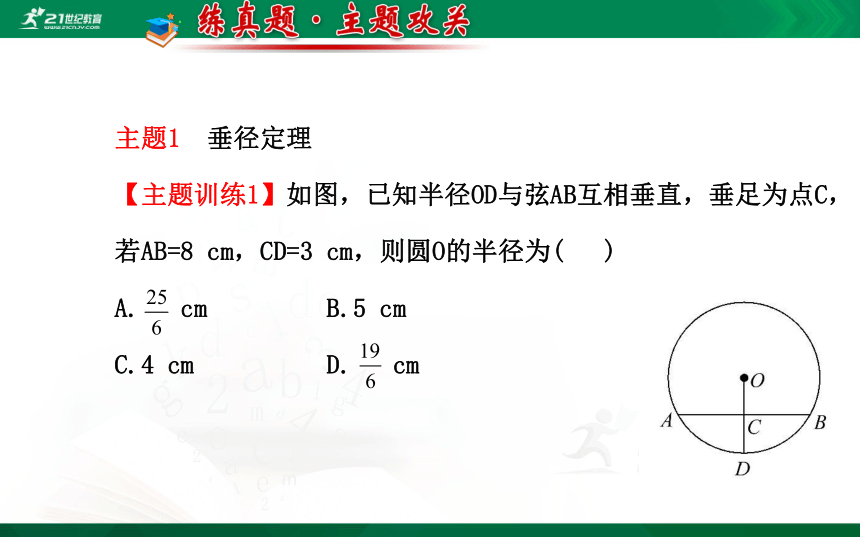
主题1 垂径定理
【主题训练1】如图,已知半径OD与弦AB互相垂直,垂足为点C,
若AB=8 cm,CD=3 cm,则圆O的半径为( )
A. cm B.5 cm
C.4 cm D. cm
【自主解答】选A.连接OA.∵OD⊥AB且OD是半径∴AC= AB
=4cm,∠OCA=90°,Rt△OAC中,设☉O的半径为R,则OA=OD=R,
OC=R-3;由勾股定理,得:OA2=AC2+OC2,即:R2=16+(R-3)2,解得
R= cm,所以选A.
【主题升华】
垂径定理及推论的四个应用
1.计算线段的长度:常利用半径、弦长的一半、圆心到弦的距离构造直角三角形,结合勾股定理进行计算.
2.证明线段相等:根据垂径定理平分线段推导线段相等.
3.证明等弧.
4.证明垂直:根据垂径定理的推论证明线段垂直.
1.如图,在☉O中,弦AB的长为8,OC⊥AB,垂足为C,且OC=3,则☉O的半径为( )
A.5 B.10 C.8 D.6
【解析】选A.连接OA,由垂径定理可得AC=4,
△OAC是直角三角形,由勾股定理可得OA2=
OC2+AC2=32+42=25,所以OA=5.
2.在☉O中,已知半径长为3,弦AB长为4,那么圆心O到AB的距离为 .
【解析】过圆心O作AB的垂线交AB于点D,
由垂径定理,得AD= AB=2,
在Rt△AOD中,运用勾股定理,得OD= .
答案:
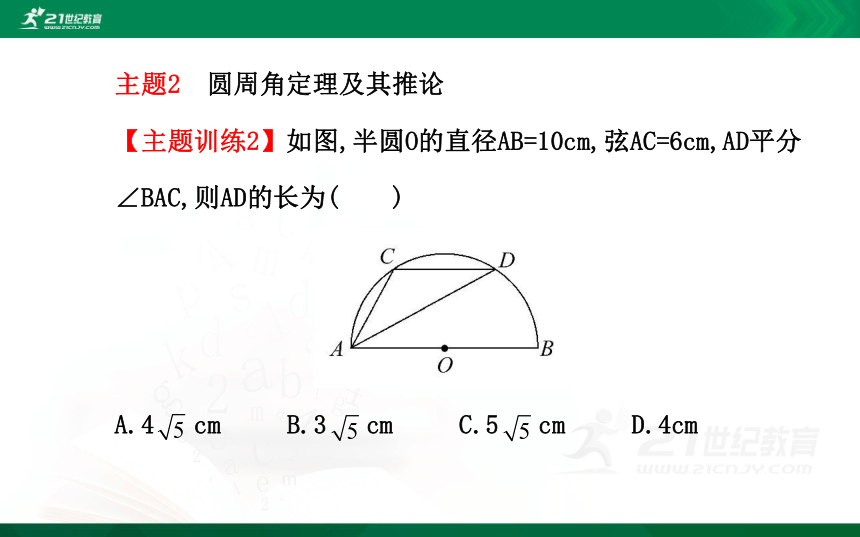
主题2 圆周角定理及其推论
【主题训练2】如图,半圆O的直径AB=10cm,弦AC=6cm,AD平分∠BAC,则AD的长为( )
A.4 cm B.3 cm C.5 cm D.4cm
【自主解答】选A.连接BC,BD,OD,
则OD,BC交于E.由于AD平分∠BAC,
所以 所以OD⊥BC,又半圆O
的直径AB=10 cm,弦AC=6 cm,所以BC=8 cm,所以BE=
4 cm,又OB=5 cm,所以OE=3 cm,所以ED=5-3=2(cm),
在Rt△BED中,BD= 又∠ADB=90°,
所以AD=
【主题升华】
圆周角的四种关系
1.同圆或等圆中,等弧对的圆周角相等.
2.同圆或等圆中,同弧或等弧所对的圆周角是圆心角的一半.
3.直径对的圆周角为90°.
4.圆内接四边形对角互补.
1.如图,在☉O中,∠ABC=50°,则∠AOC等于( )
A.50° B.80°
C.90° D.100°
【解析】选D.因为∠ABC=50°,
所以∠AOC=2∠ABC=100°.
2.(2013·郴州中考)如图,AB是☉O的直径,点C是圆上一点, ∠BAC=70°,则∠OCB= °.
【解析】因为AB是直径,所以∠ACB=90°,
又OA=OC,所以∠A=∠ACO=70°,
所以∠OCB=90°-∠ACO=90°-70°=20°.
答案:20
主题3 切线的性质和判定
【主题训练3】如图,已知AB是☉O的直径,点C,D在☉O上,点E在☉O外,∠EAC =∠B =60°.
(1)求∠ADC的度数.
(2)求证:AE是☉O的切线.
【自主解答】(1)∵∠B与∠ADC都是 所对的圆周角,且∠B =60°,
∴∠ADC=∠B =60°.
(2)∵AB是☉O的直径,
∴∠ACB=90°,
又∠B =60°,∴∠BAC=30°,
∵∠EAC =∠B =60°,
∴∠BAE =∠BAC+∠EAC=30°+60°=90°,
∴BA⊥AE,∴AE是☉O的切线.
【主题升华】
切线的性质与判定
1.切线的判定的三种方法:(1)根据定义观察直线与圆公共点的个数.(2)由圆心到直线的距离与半径的大小关系来判断.(3)应用切线的判定定理.应用判定定理时,要注意仔细审题,选择合适的证明思路:①连半径,证垂直;②作垂直,证半径.
2.切线的性质是求角的度数及垂直关系的重要依据,辅助线的作法一般是连接切点和圆心,构造垂直关系来证明或计算.切线长定理也为线段或角的相等提供了丰富的理论依据.
1.如图,在△ABC中,AB=2,AC= ,以点A为圆
心,1为半径的圆与边BC相切于点D,则∠BAC的度数是 .
【解析】如图,连接AD,则AD⊥BC;在
Rt△ABD中,AB=2,AD=1,∴∠B=30°,
因而∠BAD=60°,同理,在Rt△ACD中,
∠CAD=45°,所以∠BAC的度数是105°.
答案:105°
2.如图,AB是半圆O的直径,点P在AB的延长线上,PC切半圆O于点C,连接AC.若∠CPA=20°,则∠A= °.
【解析】如图,连接OC.∵PC切半圆O于点C,
∴PC⊥OC即∠PCO=90°.
∵∠CPA=20°,
∴∠POC=90°-∠CPA=70°.
∵OA=OC,∴∠A=∠ACO.
又∵∠POC=∠A+∠ACO.
∴∠A= ∠POC=35°.
答案:35
主题4 与圆有关的位置关系
【主题训练4】直线l与半径为r的☉O相交,且点O到直线l的距离为6,则r的取值范围是( )
A.r<6 B.r=6 C.r>6 D.r≥6
【自主解答】选C.∵直线l与☉O相交,
∴圆心O到直线l的距离d即r>d=6,故选C.
【主题升华】
与圆有关的位置关系及判定方法
1.位置关系:(1)点与圆的位置关系;(2)直线与圆的位置关系.
2.判定方法:(1)利用到圆心的距离和半径作比较;
(2)利用交点的个数判断直线与圆的位置关系.
1.已知☉O的半径是6,点O到直线l的距离为5,则直线l与☉O的位置关系是( )
A.相离 B.相切 C.相交 D.无法判断
【解析】选C.圆心到直线的距离d=5,圆的半径r=6,∴d2.在同一平面直角坐标系中有5个点:
A(1,1),B(-3,-1),C(-3,1),D(-2,-2),E(0,-3).
(1)画出△ABC的外接圆☉P,
并指出点D与☉P的位置关系.
(2)若直线l经过点D(-2,-2),
E(0,-3),判断直线l与☉P的
位置关系.
【解析】(1)所画☉P如图所示.由图可知,☉P的半径为 .
连接PD,∵PD= ∴点D在☉P上.
(2)直线l与☉P相切.
理由如下:连接PE.
∵直线l过点D(-2,-2),E(0,-3),
∴PE2=12+32=10,PD2=5,DE2=5.
∴PE2=PD2+DE2.
∴△PDE是直角三角形,且∠PDE=90°.∴PD⊥l.
∴直线l与☉P相切.
主题5 与圆有关的计算
【主题训练5】如图,AB是☉O的直径,C是半
圆O上的一点,AC平分∠DAB,AD⊥CD,垂足为D,AD交☉O于E,连
接CE.
(1)判断CD与☉O的位置关系,并证明你的结论.
(2)若E是 的中点,☉O的半径为1,求图中阴影部分的面积.
【自主解答】(1)CD与☉O相切.理由为:
∵AC为∠DAB的平分线,
∴∠DAC=∠OAC.
∵OA=OC,∴∠OAC=∠OCA,
∴∠DAC=∠OCA,
∴OC∥AD.
∵AD⊥CD,
∴OC⊥CD.∴CD与☉O相切.
(2)连接EB,由AB为直径,得到∠AEB=90°.
由(1)中AD⊥CD,OC⊥CD,∴四边形CDEF是矩形,F为EB的中点.
∴EF=DC,DE=FC,OF为△ABE的中位线.∴EF=DC=BF.
又∵E是 的中点,
∴ ∠ABE=∠EAC=∠CAB=30°.
在Rt△OBF中,∠ABE=30°.
∴OF= OB= OC=FC,FB= =EF=DC.
∵E是 的中点,∴AE=EC.
∴图中两个阴影部分的面积和等于△DCE的面积.
∴S阴影=S△DEC=
【主题升华】
与圆有关计算的四公式
1.弧长公式l= (n为弧所对的圆心角的度数,R为圆的半径).
2.扇形的面积公式S= (n为扇形的圆心角的度数,R
为圆的半径,l为扇形的弧长).
3.圆锥的侧面积S=πrl(r为圆锥的底面圆的半径,l为圆锥的母线长).
4.圆锥的全面积公式: S=πrl+πr2(S为圆锥的全面积,r为圆锥的底面圆的半径,l为圆锥的母线长).
1.用一个圆心角为120°,半径为6 cm的扇形做成一个圆锥的侧面,这个圆锥的底面的半径是( )
A.1 cm B.2 cm C.3 cm D.4 cm
【解析】选B.∵设所围圆锥的底面半径为r ,则
=2πr,∴r=2 cm.
2.一个圆锥的母线长是9,底面圆的半径是6,则这个圆锥的侧面积是( )
A.81π B.27π C.54π D.18π
【解析】选C.方法一:S圆锥的侧面积= Rl= ×6×2π×9=
54π,
方法二:S圆锥的侧面积=πrl=6×9π=54π.
复习课件
主题1 垂径定理
【主题训练1】如图,已知半径OD与弦AB互相垂直,垂足为点C,
若AB=8 cm,CD=3 cm,则圆O的半径为( )
A. cm B.5 cm
C.4 cm D. cm
【自主解答】选A.连接OA.∵OD⊥AB且OD是半径∴AC= AB
=4cm,∠OCA=90°,Rt△OAC中,设☉O的半径为R,则OA=OD=R,
OC=R-3;由勾股定理,得:OA2=AC2+OC2,即:R2=16+(R-3)2,解得
R= cm,所以选A.
【主题升华】
垂径定理及推论的四个应用
1.计算线段的长度:常利用半径、弦长的一半、圆心到弦的距离构造直角三角形,结合勾股定理进行计算.
2.证明线段相等:根据垂径定理平分线段推导线段相等.
3.证明等弧.
4.证明垂直:根据垂径定理的推论证明线段垂直.
1.如图,在☉O中,弦AB的长为8,OC⊥AB,垂足为C,且OC=3,则☉O的半径为( )
A.5 B.10 C.8 D.6
【解析】选A.连接OA,由垂径定理可得AC=4,
△OAC是直角三角形,由勾股定理可得OA2=
OC2+AC2=32+42=25,所以OA=5.
2.在☉O中,已知半径长为3,弦AB长为4,那么圆心O到AB的距离为 .
【解析】过圆心O作AB的垂线交AB于点D,
由垂径定理,得AD= AB=2,
在Rt△AOD中,运用勾股定理,得OD= .
答案:
主题2 圆周角定理及其推论
【主题训练2】如图,半圆O的直径AB=10cm,弦AC=6cm,AD平分∠BAC,则AD的长为( )
A.4 cm B.3 cm C.5 cm D.4cm
【自主解答】选A.连接BC,BD,OD,
则OD,BC交于E.由于AD平分∠BAC,
所以 所以OD⊥BC,又半圆O
的直径AB=10 cm,弦AC=6 cm,所以BC=8 cm,所以BE=
4 cm,又OB=5 cm,所以OE=3 cm,所以ED=5-3=2(cm),
在Rt△BED中,BD= 又∠ADB=90°,
所以AD=
【主题升华】
圆周角的四种关系
1.同圆或等圆中,等弧对的圆周角相等.
2.同圆或等圆中,同弧或等弧所对的圆周角是圆心角的一半.
3.直径对的圆周角为90°.
4.圆内接四边形对角互补.
1.如图,在☉O中,∠ABC=50°,则∠AOC等于( )
A.50° B.80°
C.90° D.100°
【解析】选D.因为∠ABC=50°,
所以∠AOC=2∠ABC=100°.
2.(2013·郴州中考)如图,AB是☉O的直径,点C是圆上一点, ∠BAC=70°,则∠OCB= °.
【解析】因为AB是直径,所以∠ACB=90°,
又OA=OC,所以∠A=∠ACO=70°,
所以∠OCB=90°-∠ACO=90°-70°=20°.
答案:20
主题3 切线的性质和判定
【主题训练3】如图,已知AB是☉O的直径,点C,D在☉O上,点E在☉O外,∠EAC =∠B =60°.
(1)求∠ADC的度数.
(2)求证:AE是☉O的切线.
【自主解答】(1)∵∠B与∠ADC都是 所对的圆周角,且∠B =60°,
∴∠ADC=∠B =60°.
(2)∵AB是☉O的直径,
∴∠ACB=90°,
又∠B =60°,∴∠BAC=30°,
∵∠EAC =∠B =60°,
∴∠BAE =∠BAC+∠EAC=30°+60°=90°,
∴BA⊥AE,∴AE是☉O的切线.
【主题升华】
切线的性质与判定
1.切线的判定的三种方法:(1)根据定义观察直线与圆公共点的个数.(2)由圆心到直线的距离与半径的大小关系来判断.(3)应用切线的判定定理.应用判定定理时,要注意仔细审题,选择合适的证明思路:①连半径,证垂直;②作垂直,证半径.
2.切线的性质是求角的度数及垂直关系的重要依据,辅助线的作法一般是连接切点和圆心,构造垂直关系来证明或计算.切线长定理也为线段或角的相等提供了丰富的理论依据.
1.如图,在△ABC中,AB=2,AC= ,以点A为圆
心,1为半径的圆与边BC相切于点D,则∠BAC的度数是 .
【解析】如图,连接AD,则AD⊥BC;在
Rt△ABD中,AB=2,AD=1,∴∠B=30°,
因而∠BAD=60°,同理,在Rt△ACD中,
∠CAD=45°,所以∠BAC的度数是105°.
答案:105°
2.如图,AB是半圆O的直径,点P在AB的延长线上,PC切半圆O于点C,连接AC.若∠CPA=20°,则∠A= °.
【解析】如图,连接OC.∵PC切半圆O于点C,
∴PC⊥OC即∠PCO=90°.
∵∠CPA=20°,
∴∠POC=90°-∠CPA=70°.
∵OA=OC,∴∠A=∠ACO.
又∵∠POC=∠A+∠ACO.
∴∠A= ∠POC=35°.
答案:35
主题4 与圆有关的位置关系
【主题训练4】直线l与半径为r的☉O相交,且点O到直线l的距离为6,则r的取值范围是( )
A.r<6 B.r=6 C.r>6 D.r≥6
【自主解答】选C.∵直线l与☉O相交,
∴圆心O到直线l的距离d
【主题升华】
与圆有关的位置关系及判定方法
1.位置关系:(1)点与圆的位置关系;(2)直线与圆的位置关系.
2.判定方法:(1)利用到圆心的距离和半径作比较;
(2)利用交点的个数判断直线与圆的位置关系.
1.已知☉O的半径是6,点O到直线l的距离为5,则直线l与☉O的位置关系是( )
A.相离 B.相切 C.相交 D.无法判断
【解析】选C.圆心到直线的距离d=5,圆的半径r=6,∴d
A(1,1),B(-3,-1),C(-3,1),D(-2,-2),E(0,-3).
(1)画出△ABC的外接圆☉P,
并指出点D与☉P的位置关系.
(2)若直线l经过点D(-2,-2),
E(0,-3),判断直线l与☉P的
位置关系.
【解析】(1)所画☉P如图所示.由图可知,☉P的半径为 .
连接PD,∵PD= ∴点D在☉P上.
(2)直线l与☉P相切.
理由如下:连接PE.
∵直线l过点D(-2,-2),E(0,-3),
∴PE2=12+32=10,PD2=5,DE2=5.
∴PE2=PD2+DE2.
∴△PDE是直角三角形,且∠PDE=90°.∴PD⊥l.
∴直线l与☉P相切.
主题5 与圆有关的计算
【主题训练5】如图,AB是☉O的直径,C是半
圆O上的一点,AC平分∠DAB,AD⊥CD,垂足为D,AD交☉O于E,连
接CE.
(1)判断CD与☉O的位置关系,并证明你的结论.
(2)若E是 的中点,☉O的半径为1,求图中阴影部分的面积.
【自主解答】(1)CD与☉O相切.理由为:
∵AC为∠DAB的平分线,
∴∠DAC=∠OAC.
∵OA=OC,∴∠OAC=∠OCA,
∴∠DAC=∠OCA,
∴OC∥AD.
∵AD⊥CD,
∴OC⊥CD.∴CD与☉O相切.
(2)连接EB,由AB为直径,得到∠AEB=90°.
由(1)中AD⊥CD,OC⊥CD,∴四边形CDEF是矩形,F为EB的中点.
∴EF=DC,DE=FC,OF为△ABE的中位线.∴EF=DC=BF.
又∵E是 的中点,
∴ ∠ABE=∠EAC=∠CAB=30°.
在Rt△OBF中,∠ABE=30°.
∴OF= OB= OC=FC,FB= =EF=DC.
∵E是 的中点,∴AE=EC.
∴图中两个阴影部分的面积和等于△DCE的面积.
∴S阴影=S△DEC=
【主题升华】
与圆有关计算的四公式
1.弧长公式l= (n为弧所对的圆心角的度数,R为圆的半径).
2.扇形的面积公式S= (n为扇形的圆心角的度数,R
为圆的半径,l为扇形的弧长).
3.圆锥的侧面积S=πrl(r为圆锥的底面圆的半径,l为圆锥的母线长).
4.圆锥的全面积公式: S=πrl+πr2(S为圆锥的全面积,r为圆锥的底面圆的半径,l为圆锥的母线长).
1.用一个圆心角为120°,半径为6 cm的扇形做成一个圆锥的侧面,这个圆锥的底面的半径是( )
A.1 cm B.2 cm C.3 cm D.4 cm
【解析】选B.∵设所围圆锥的底面半径为r ,则
=2πr,∴r=2 cm.
2.一个圆锥的母线长是9,底面圆的半径是6,则这个圆锥的侧面积是( )
A.81π B.27π C.54π D.18π
【解析】选C.方法一:S圆锥的侧面积= Rl= ×6×2π×9=
54π,
方法二:S圆锥的侧面积=πrl=6×9π=54π.
