人教版数学九年级上册24.1.4圆周角教案(表格式)
文档属性
| 名称 | 人教版数学九年级上册24.1.4圆周角教案(表格式) |

|
|
| 格式 | docx | ||
| 文件大小 | 59.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-11 00:00:00 | ||
图片预览

文档简介
教师姓名
单位名称
填写时间
学科
数学
年级/册
九年级上册
教材版本
人教版
课题名称
24.1.4圆周角
难点名称
难点:了解圆周角的分类、用化归思想合情推理验证“圆周角与圆心角的关系”
突破难点的方法:
观察发现,总结方法。
难点分析
从知识角度分析为什么难
圆周角定理推理:在同圆或等圆中,同弧或等弧所对的圆周角相等。
从学生角度分析为什么难
学生的角度看圆周角的定理证明和应用比较难,还有同一条弧所对的圆周角相等推理的应用
难点教学方法
填写示例
老师当场测量角的度数做演示让学生理解,
用课件插入辅助线用简单的方法给学生讲解引导学生证明,然后用简单的练习来巩固。
教学环节
教学过程
导入
1、复习提问:课件图中的∠AOB是我们前面学习过的什么角?
2、什么是圆心角?
答:顶点在圆心的角叫圆心角.
3、引题圆周角:
如果顶点不在圆心而在圆上,则得到如右图的新的角
∠BAC,它就是圆周角.(如右图)
(演示图形,提出圆周角的定义)
(板书)课题
定义:顶点在圆周上,并且两边都和圆相交的角叫做圆周角.
知识讲解
(难点突破)
(1)观察发现,猜想结论
测量图中
∠BAC和
∠BOC的度数。它们之间有什么关系?
学生分组测量、讨论后请学生代表说出本组的猜想:圆周角大小等于圆心角的一半,由于测量存在误差,因此实验、观察等方法得出的猜想的正确性是需要进一步验证。老师当场测量给学生演示证明
(2)总结规律,得出定理
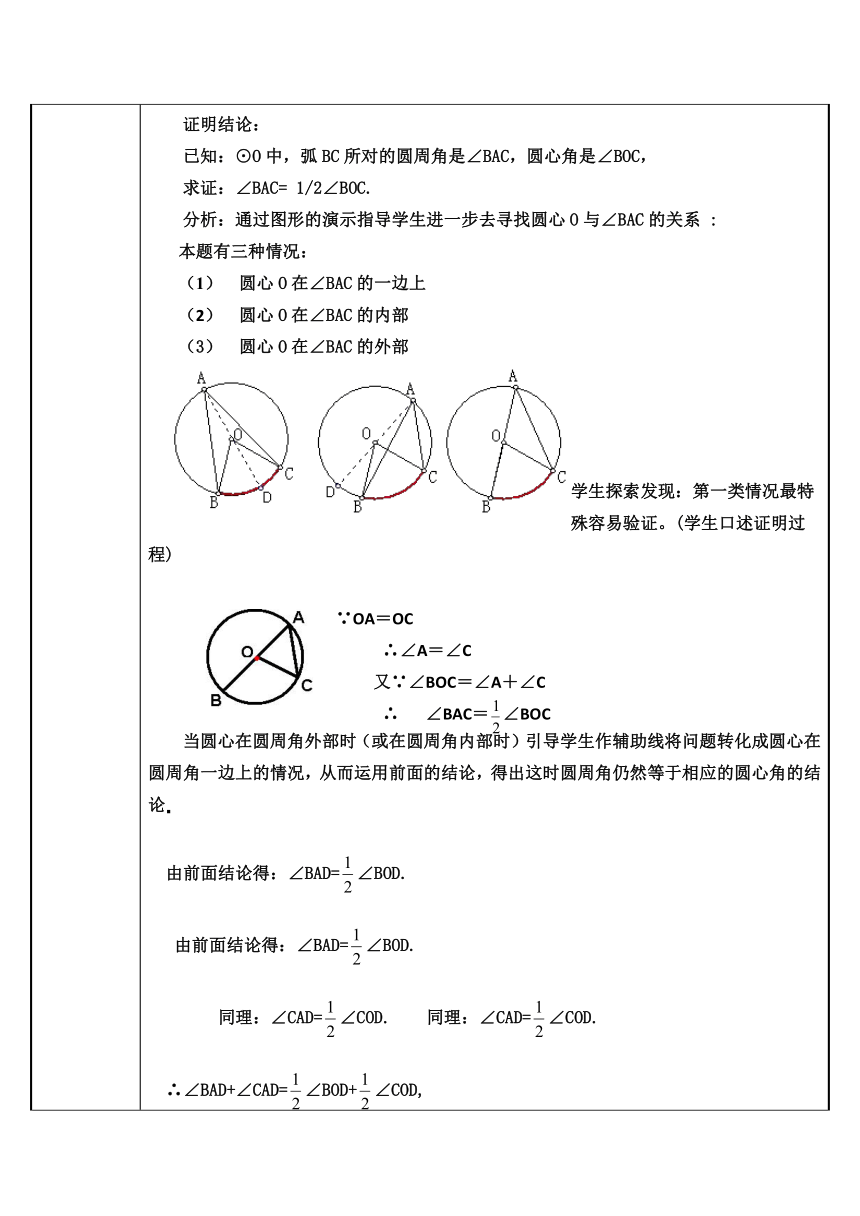
证明结论:
已知:⊙O中,弧BC所对的圆周角是∠BAC,圆心角是∠BOC,
求证:∠BAC=
1/2∠BOC.
分析:通过图形的演示指导学生进一步去寻找圆心O与∠BAC的关系
:
本题有三种情况:
圆心O在∠BAC的一边上
圆心O在∠BAC的内部
圆心O在∠BAC的外部
学生探索发现:第一类情况最特殊容易验证。(学生口述证明过程)
∵OA=OC
∴∠A=∠C
又∵∠BOC=∠A+∠C
∴
∠BAC=∠BOC
当圆心在圆周角外部时(或在圆周角内部时)引导学生作辅助线将问题转化成圆心在圆周角一边上的情况,从而运用前面的结论,得出这时圆周角仍然等于相应的圆心角的结论.
由前面结论得:∠BAD=∠BOD.
由前面结论得:∠BAD=∠BOD.
同理:∠CAD=∠COD.
同理:∠CAD=∠COD.
∴∠BAD+∠CAD=∠BOD+∠COD,
∴∠CAD-∠BAD
=∠COD-∠BOD,
即:∠BAC=∠BOC.
学生完成由定理证明,培养严谨的思维品质。
小结:通过圆周角定理的证明,我们知道有一些命题的证明是要分情况来逐一进行讨论的,大家应该明确,要不要分情况证明,主要看各种情况的证明方法是否相同,如果相同,则不需要分情况证明,如果不同,则必须分情况证明,即不能重复,也不能遗漏。
结论:同弧所对的圆周角的度数等于这条弧所对的圆心角的度数的一半。
活动2:观察图形,总结归纳
问题1:半圆(或直径)所对的圆周角是多少度?(课件:圆周角定理推论)(学生观察图形,得到结论)
圆周角定理推理:
半圆(或直径)所对的圆周角是直角;
90°的圆周角所对的弦是直径。
练习:
如图,AB是⊙O的直径,点C在⊙O上
若∠A=40
?,则∠B的度数为(
)
A.80
?
B.60
?
C.50
?
D.40
?
四、
分层练习
巩固提高
1、如图,点A、B、C在圆O上,∠A=60°,则∠BOC
=
度.
五、反思小结
布置作业
小结反思
这节课我们主要学习了哪些知识?
解决问题中,我们应用了哪些数学思想方法?
你还有哪些收获?
课堂练习
(难点巩固)
1.图,A、B、C三点在⊙O上,∠AOB=100°,则∠ACB等于(
)
A.100°
B.80°
C.50°
D.40°
2.如图,点A、B、C在⊙O上,
2.(1)
若∠BAC=70°,则∠BOC=____°
(2)
若∠AOB=100°,则∠ACB=____°.
3.如左图,点A、B、C、D在⊙O上,点A与点D在点B、C所在直线的同侧,∠BAC=40°
(1)∠BDC=_______°
(2)∠BOC=_______°
4.如右图,∠A是⊙O的圆周角,∠A=40°,则∠OBC=_______°
小结
单位名称
填写时间
学科
数学
年级/册
九年级上册
教材版本
人教版
课题名称
24.1.4圆周角
难点名称
难点:了解圆周角的分类、用化归思想合情推理验证“圆周角与圆心角的关系”
突破难点的方法:
观察发现,总结方法。
难点分析
从知识角度分析为什么难
圆周角定理推理:在同圆或等圆中,同弧或等弧所对的圆周角相等。
从学生角度分析为什么难
学生的角度看圆周角的定理证明和应用比较难,还有同一条弧所对的圆周角相等推理的应用
难点教学方法
填写示例
老师当场测量角的度数做演示让学生理解,
用课件插入辅助线用简单的方法给学生讲解引导学生证明,然后用简单的练习来巩固。
教学环节
教学过程
导入
1、复习提问:课件图中的∠AOB是我们前面学习过的什么角?
2、什么是圆心角?
答:顶点在圆心的角叫圆心角.
3、引题圆周角:
如果顶点不在圆心而在圆上,则得到如右图的新的角
∠BAC,它就是圆周角.(如右图)
(演示图形,提出圆周角的定义)
(板书)课题
定义:顶点在圆周上,并且两边都和圆相交的角叫做圆周角.
知识讲解
(难点突破)
(1)观察发现,猜想结论
测量图中
∠BAC和
∠BOC的度数。它们之间有什么关系?
学生分组测量、讨论后请学生代表说出本组的猜想:圆周角大小等于圆心角的一半,由于测量存在误差,因此实验、观察等方法得出的猜想的正确性是需要进一步验证。老师当场测量给学生演示证明
(2)总结规律,得出定理
证明结论:
已知:⊙O中,弧BC所对的圆周角是∠BAC,圆心角是∠BOC,
求证:∠BAC=
1/2∠BOC.
分析:通过图形的演示指导学生进一步去寻找圆心O与∠BAC的关系
:
本题有三种情况:
圆心O在∠BAC的一边上
圆心O在∠BAC的内部
圆心O在∠BAC的外部
学生探索发现:第一类情况最特殊容易验证。(学生口述证明过程)
∵OA=OC
∴∠A=∠C
又∵∠BOC=∠A+∠C
∴
∠BAC=∠BOC
当圆心在圆周角外部时(或在圆周角内部时)引导学生作辅助线将问题转化成圆心在圆周角一边上的情况,从而运用前面的结论,得出这时圆周角仍然等于相应的圆心角的结论.
由前面结论得:∠BAD=∠BOD.
由前面结论得:∠BAD=∠BOD.
同理:∠CAD=∠COD.
同理:∠CAD=∠COD.
∴∠BAD+∠CAD=∠BOD+∠COD,
∴∠CAD-∠BAD
=∠COD-∠BOD,
即:∠BAC=∠BOC.
学生完成由定理证明,培养严谨的思维品质。
小结:通过圆周角定理的证明,我们知道有一些命题的证明是要分情况来逐一进行讨论的,大家应该明确,要不要分情况证明,主要看各种情况的证明方法是否相同,如果相同,则不需要分情况证明,如果不同,则必须分情况证明,即不能重复,也不能遗漏。
结论:同弧所对的圆周角的度数等于这条弧所对的圆心角的度数的一半。
活动2:观察图形,总结归纳
问题1:半圆(或直径)所对的圆周角是多少度?(课件:圆周角定理推论)(学生观察图形,得到结论)
圆周角定理推理:
半圆(或直径)所对的圆周角是直角;
90°的圆周角所对的弦是直径。
练习:
如图,AB是⊙O的直径,点C在⊙O上
若∠A=40
?,则∠B的度数为(
)
A.80
?
B.60
?
C.50
?
D.40
?
四、
分层练习
巩固提高
1、如图,点A、B、C在圆O上,∠A=60°,则∠BOC
=
度.
五、反思小结
布置作业
小结反思
这节课我们主要学习了哪些知识?
解决问题中,我们应用了哪些数学思想方法?
你还有哪些收获?
课堂练习
(难点巩固)
1.图,A、B、C三点在⊙O上,∠AOB=100°,则∠ACB等于(
)
A.100°
B.80°
C.50°
D.40°
2.如图,点A、B、C在⊙O上,
2.(1)
若∠BAC=70°,则∠BOC=____°
(2)
若∠AOB=100°,则∠ACB=____°.
3.如左图,点A、B、C、D在⊙O上,点A与点D在点B、C所在直线的同侧,∠BAC=40°
(1)∠BDC=_______°
(2)∠BOC=_______°
4.如右图,∠A是⊙O的圆周角,∠A=40°,则∠OBC=_______°
小结
同课章节目录
