冀教版六年级数学下册6.2.3 图形的运动 课件(24张ppt)
文档属性
| 名称 | 冀教版六年级数学下册6.2.3 图形的运动 课件(24张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 6.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-10 20:50:56 | ||
图片预览





文档简介
图形与几何
第4课时 图形的运动
1.结合具体事例,经历复习总结“图形的运动”有关知识的过程。
2.进一步感受生活中的对称、平移、旋转现象,掌握方格纸上画轴对称图形的另一半、将简单图形平移或旋转90°,以及按比例放大或缩小图形的方法。
3.在观察、画图、交流等活动中,进一步发展空间观念。
【重点】能运用轴对称、平移、旋转放大与缩小的特征进行图形的变换。
【难点】利用轴对称、平移、旋转、放大与缩小的特征进行图形变换。
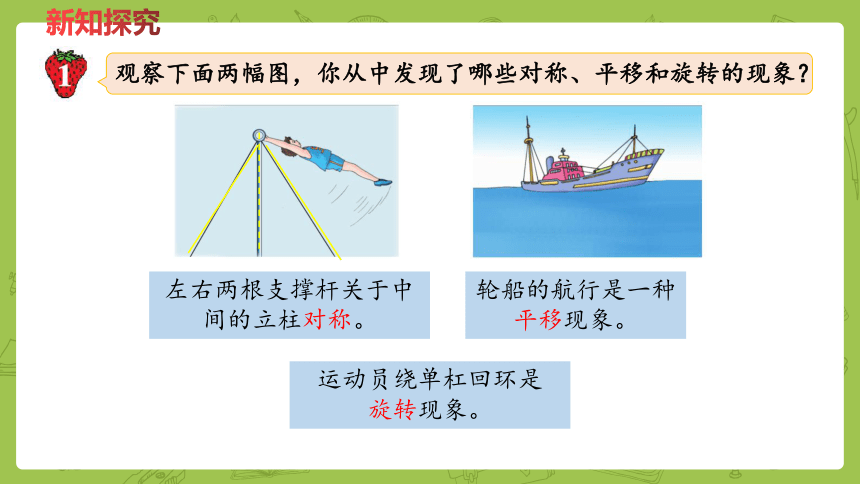
观察下面两幅图,你从中发现了哪些对称、平移和旋转的现象?
左右两根支撑杆关于中间的立柱对称。
轮船的航行是一种
平移现象。
运动员绕单杠回环是
旋转现象。
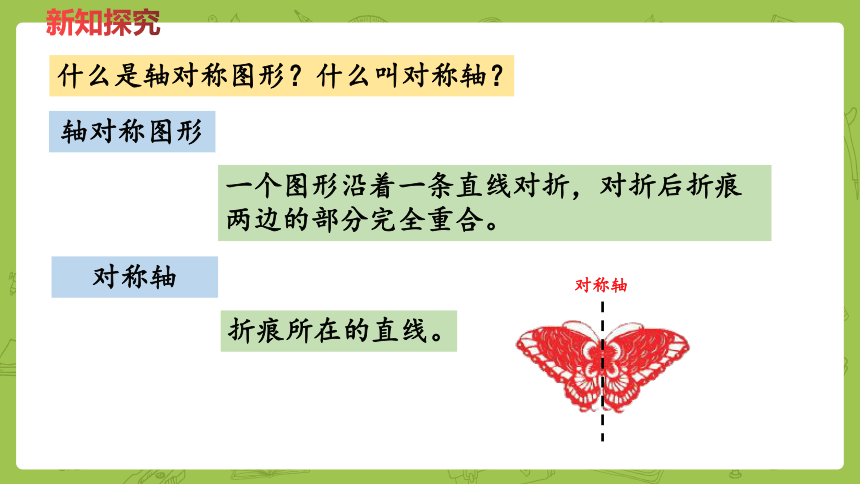
什么是轴对称图形?什么叫对称轴?
轴对称图形
一个图形沿着一条直线对折,对折后折痕两边的部分完全重合。
对称轴
折痕所在的直线。
对称轴
生活中的轴对称图形。
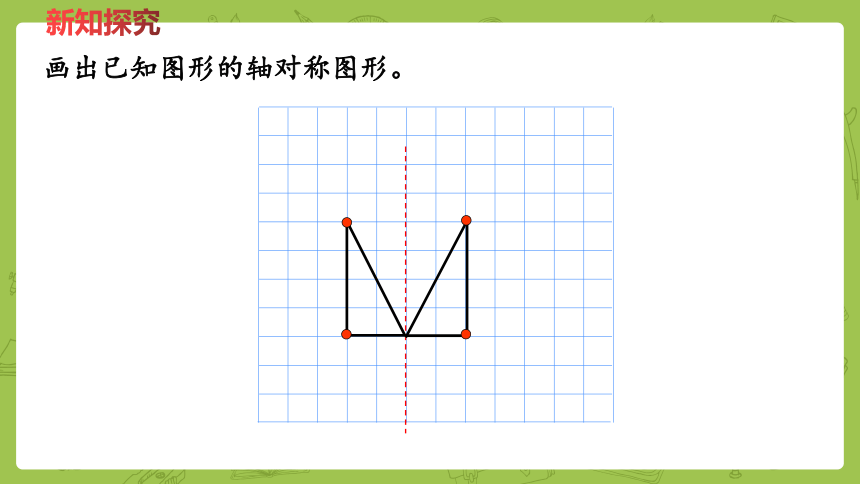
画出已知图形的轴对称图形。
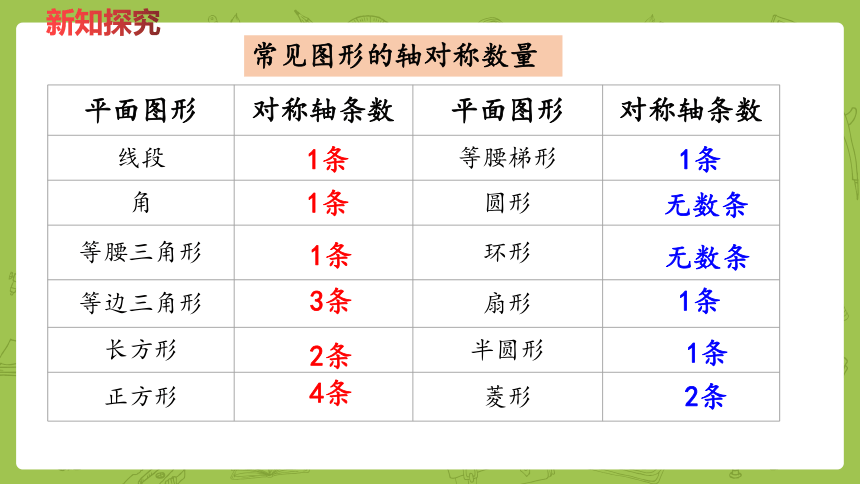
{8799B23B-EC83-4686-B30A-512413B5E67A}平面图形
对称轴条数
平面图形
对称轴条数
线段
等腰梯形
角
圆形
等腰三角形
环形
等边三角形
扇形
长方形
半圆形
正方形
菱形
1条
2条
4条
无数条
1条
1条
1条
无数条
1条
2条
常见图形的轴对称数量
1条
3条
什么是平移?判断的关键是什么?
平移
在同一平面内,将一个图形沿某个方向移动一定的距离,这样的运动叫做图形的平移。
判断关键
一是平移的方向,二是平移的距离。
平移的特点
平移不改变图形的大小和形状,只是图形的位置发生变化。
生活中的平移。
什么是旋转?旋转的关键是什么?
旋转
在平面内,一个图形绕一点沿一定方向转动一定角度,这样的运动叫图形的旋转。
旋转关键
一是中心点,二是旋转方向,三是旋转角度。
旋转的特点
不改变图形的形状和大小。只是图形的位置发生改变。
生活中的旋转。
{8799B23B-EC83-4686-B30A-512413B5E67A}
意 义
特 点
画 法
要 素
一个图形,如果沿一条直线对折,直线两边的部分能够完全重合,这样的图形叫做轴对称图形。折痕所在的这条直线叫做对称轴。
对称轴两侧相对的点到对称轴的距离相等。
先确定各对称点的位置,再连线。
在同一平面内,将一个图形沿某个方向移动一定的距离,这样的运动叫做图形的平移。
平移不改变图形的大小和形状,只是图形的位置发生变化。
一是移动的方向,二是移动的距离。
要先确定方向,再确定平移的距离。
在平面内,一个图形绕一点沿一定方向转动一定角度,这样的运动叫图形的旋转。
不改变图形的形状和大小。只是图形的位置发生改变。
一是中心点,二是旋转方向,三是旋转角度。
先弄清楚旋转的方向与角度,然后围绕中心点进行旋转。
轴对称
平移
在
旋转
对称轴
轴对称、旋转和平移
{8799B23B-EC83-4686-B30A-512413B5E67A}
意 义
特 点
画 法
按照一定比例,将一个图形缩小或放大,叫做图形的缩放。
①图形的放大:比值大于1,如2:1。
1.看比例,确定放大还是缩小。
2.算出放大或缩小后图形对应的边长。
3.画出图形。
②图形的缩小:比值小于1,如1:3。
图形的放大与缩小
图形运动之间的异同点
{8799B23B-EC83-4686-B30A-512413B5E67A}名称
平移与旋转
图形的放大与缩小
不同点
相同点
不改变图形的形状和大小,只改变图形的位置。
不改变图形的形状,只改变图形的大小。
都不改变图形的形状。
按要求在方格纸上画图。
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
①
②
A
B
C
D
(1)根据对称轴的位置画出上面两个轴对称图形的另一半。
(2)将画好的图形①再向下平移5格。
(3)将画好的图形②绕A点逆时针旋转90°。
按要求在方格纸上画图。
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
4cm
4cm
6cm
将图形的每条边放大到原来的2倍。
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
6cm
9cm
6cm
4cm
将图形的长和宽缩小到原来的 。
3
2
1.下面是用纸做成的小旗,想象一下,快速旋转小棒,小旗转动一周会形成哪个图形,用线连起来。
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
①
②
图①面积:
1×12=12平方厘米
图②面积:
(4+10)×2÷2+4 ×3+
4 ×3÷2
=14+12+6
=32平方厘米
2.完成下面的轴对称图形,并计算每个图形的面积。(每个方格的边长表示1厘米)
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
3.将图形向右平移四格。
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
4.将图形B绕点M顺时针旋转90°。
.
B
M
5.以虚线为对称轴,分别画出轴对称图形。
6.(1)将图A绕点O顺时针旋转90°得到图形B。
(2)将图形B再向下平移3格,得到图形C。
(3)以直线L为对称轴,作图形C的轴对称图形,得到图形D。
A
L
O
B
C
D
由A到B是经过向右平移5个格得到的。
由B到C先向右平移5个格,再绕中心点逆时针旋转90°得到的。
或者先逆时针旋转90°,再向右平移5个格得到的。
由C到D先向右平移5个格,再绕中心点逆时针旋转90°得到的。
或者先绕中心点旋转90°,在向右平移5个格得到的。
7.图中A→B→C →D 是怎样变过来的?
这节课你有什么收获?
图形的运动
完成对应练习
第4课时 图形的运动
1.结合具体事例,经历复习总结“图形的运动”有关知识的过程。
2.进一步感受生活中的对称、平移、旋转现象,掌握方格纸上画轴对称图形的另一半、将简单图形平移或旋转90°,以及按比例放大或缩小图形的方法。
3.在观察、画图、交流等活动中,进一步发展空间观念。
【重点】能运用轴对称、平移、旋转放大与缩小的特征进行图形的变换。
【难点】利用轴对称、平移、旋转、放大与缩小的特征进行图形变换。
观察下面两幅图,你从中发现了哪些对称、平移和旋转的现象?
左右两根支撑杆关于中间的立柱对称。
轮船的航行是一种
平移现象。
运动员绕单杠回环是
旋转现象。
什么是轴对称图形?什么叫对称轴?
轴对称图形
一个图形沿着一条直线对折,对折后折痕两边的部分完全重合。
对称轴
折痕所在的直线。
对称轴
生活中的轴对称图形。
画出已知图形的轴对称图形。
{8799B23B-EC83-4686-B30A-512413B5E67A}平面图形
对称轴条数
平面图形
对称轴条数
线段
等腰梯形
角
圆形
等腰三角形
环形
等边三角形
扇形
长方形
半圆形
正方形
菱形
1条
2条
4条
无数条
1条
1条
1条
无数条
1条
2条
常见图形的轴对称数量
1条
3条
什么是平移?判断的关键是什么?
平移
在同一平面内,将一个图形沿某个方向移动一定的距离,这样的运动叫做图形的平移。
判断关键
一是平移的方向,二是平移的距离。
平移的特点
平移不改变图形的大小和形状,只是图形的位置发生变化。
生活中的平移。
什么是旋转?旋转的关键是什么?
旋转
在平面内,一个图形绕一点沿一定方向转动一定角度,这样的运动叫图形的旋转。
旋转关键
一是中心点,二是旋转方向,三是旋转角度。
旋转的特点
不改变图形的形状和大小。只是图形的位置发生改变。
生活中的旋转。
{8799B23B-EC83-4686-B30A-512413B5E67A}
意 义
特 点
画 法
要 素
一个图形,如果沿一条直线对折,直线两边的部分能够完全重合,这样的图形叫做轴对称图形。折痕所在的这条直线叫做对称轴。
对称轴两侧相对的点到对称轴的距离相等。
先确定各对称点的位置,再连线。
在同一平面内,将一个图形沿某个方向移动一定的距离,这样的运动叫做图形的平移。
平移不改变图形的大小和形状,只是图形的位置发生变化。
一是移动的方向,二是移动的距离。
要先确定方向,再确定平移的距离。
在平面内,一个图形绕一点沿一定方向转动一定角度,这样的运动叫图形的旋转。
不改变图形的形状和大小。只是图形的位置发生改变。
一是中心点,二是旋转方向,三是旋转角度。
先弄清楚旋转的方向与角度,然后围绕中心点进行旋转。
轴对称
平移
在
旋转
对称轴
轴对称、旋转和平移
{8799B23B-EC83-4686-B30A-512413B5E67A}
意 义
特 点
画 法
按照一定比例,将一个图形缩小或放大,叫做图形的缩放。
①图形的放大:比值大于1,如2:1。
1.看比例,确定放大还是缩小。
2.算出放大或缩小后图形对应的边长。
3.画出图形。
②图形的缩小:比值小于1,如1:3。
图形的放大与缩小
图形运动之间的异同点
{8799B23B-EC83-4686-B30A-512413B5E67A}名称
平移与旋转
图形的放大与缩小
不同点
相同点
不改变图形的形状和大小,只改变图形的位置。
不改变图形的形状,只改变图形的大小。
都不改变图形的形状。
按要求在方格纸上画图。
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
①
②
A
B
C
D
(1)根据对称轴的位置画出上面两个轴对称图形的另一半。
(2)将画好的图形①再向下平移5格。
(3)将画好的图形②绕A点逆时针旋转90°。
按要求在方格纸上画图。
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
4cm
4cm
6cm
将图形的每条边放大到原来的2倍。
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
6cm
9cm
6cm
4cm
将图形的长和宽缩小到原来的 。
3
2
1.下面是用纸做成的小旗,想象一下,快速旋转小棒,小旗转动一周会形成哪个图形,用线连起来。
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
①
②
图①面积:
1×12=12平方厘米
图②面积:
(4+10)×2÷2+4 ×3+
4 ×3÷2
=14+12+6
=32平方厘米
2.完成下面的轴对称图形,并计算每个图形的面积。(每个方格的边长表示1厘米)
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
3.将图形向右平移四格。
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
4.将图形B绕点M顺时针旋转90°。
.
B
M
5.以虚线为对称轴,分别画出轴对称图形。
6.(1)将图A绕点O顺时针旋转90°得到图形B。
(2)将图形B再向下平移3格,得到图形C。
(3)以直线L为对称轴,作图形C的轴对称图形,得到图形D。
A
L
O
B
C
D
由A到B是经过向右平移5个格得到的。
由B到C先向右平移5个格,再绕中心点逆时针旋转90°得到的。
或者先逆时针旋转90°,再向右平移5个格得到的。
由C到D先向右平移5个格,再绕中心点逆时针旋转90°得到的。
或者先绕中心点旋转90°,在向右平移5个格得到的。
7.图中A→B→C →D 是怎样变过来的?
这节课你有什么收获?
图形的运动
完成对应练习
