冀教版 八年级数学下册 第20章 函数 单元达标测试卷(word版 含答案)
文档属性
| 名称 | 冀教版 八年级数学下册 第20章 函数 单元达标测试卷(word版 含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 979.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-10 00:00:00 | ||
图片预览





文档简介
第20章达标测试卷
一、选择题(1~10题每题3分,11~16题每题2分,共42分)
1.一本笔记本3元,买x本需要y元,在这一问题中,自变量是( )
A.笔记本 B.3 C.x D.y
2.下列表达式中,当x=2时,y=1的是( )
A.y=x+3 B.y=x-1
C.y=x-3 D.y=-x-1
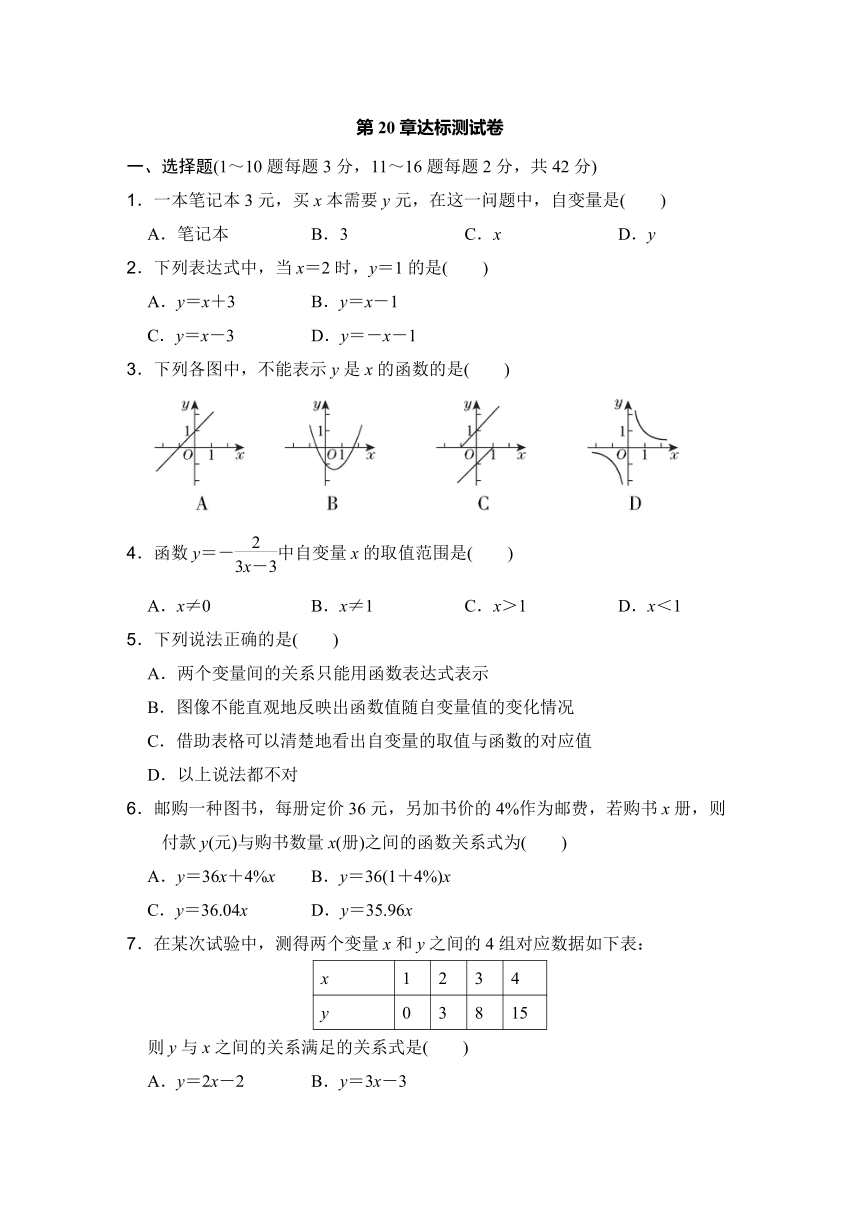
3.下列各图中,不能表示y是x的函数的是( )
4.函数y=-中自变量x的取值范围是( )
A.x≠0 B.x≠1 C.x>1 D.x<1
5.下列说法正确的是( )
A.两个变量间的关系只能用函数表达式表示
B.图像不能直观地反映出函数值随自变量值的变化情况
C.借助表格可以清楚地看出自变量的取值与函数的对应值
D.以上说法都不对
6.邮购一种图书,每册定价36元,另加书价的4%作为邮费,若购书x册,则付款y(元)与购书数量x(册)之间的函数关系式为( )
A.y=36x+4%x B.y=36(1+4%)x
C.y=36.04x D.y=35.96x
7.在某次试验中,测得两个变量x和y之间的4组对应数据如下表:
x 1 2 3 4
y 0 3 8 15
则y与x之间的关系满足的关系式是( )
A.y=2x-2 B.y=3x-3
C.y=x2-1 D.y=x+1
8.电话卡上有4元话费,通话时每分收0.4元话费,则电话卡上的余额y(元)与通话时间t(分)之间的函数图像是( )
A B C D
9.如图是某型号新能源纯电动汽车充满电后,蓄电池剩余电量y(千瓦时)与已行驶路程x(千米)之间的函数图像.下列说法错误的是( )
A.该汽车的蓄电池充满电时,电量是60千瓦时
B.蓄电池剩余电量为35千瓦时时,汽车已行驶了150千米
C.当汽车已行驶180千米时,蓄电池的剩余电量为20千瓦时
D.25千瓦时的电量,汽车能行驶150千米
(第9题) (第12题)
10.函数y=中自变量x的取值范围是( )
A.x<4 B.x≠4 C.x>4 D.x≤4
11.一司机驾驶汽车从甲地去乙地,他以80 km/h的平均速度用2 h到达目的地,当他按原路匀速返回时,汽车的速度v与时间t的函数关系是( )
A.v= B.v= C.v= D.v=
12.某学校组织团员举行“伏羲文化旅游节”宣传活动,从学校骑自行车出发,先上坡到达甲地后,宣传了8分钟,然后下坡到乙地又宣传了8分钟返回,行程情况如图所示.若返回时,上、下坡速度保持不变,在甲地仍要宣传8分钟,那么他们从乙地返回学校所用的时间是( )
A.33分钟 B.46分钟 C.48分钟 D.45.2分钟
13.根据如图所示的程序计算函数y的值,若输入x的值是7,则输出y的值是-2,若输入x的值是-8,则输出y的值是( )
(第13题)
A.5 B.10 C.19 D.21
14.实践证明1分钟跳绳测验的最佳状态是前20秒速度匀速增加,后10秒冲刺,中间速度保持不变,则跳绳速度v(个/秒)与时间t(秒)之间的函数图像大致为( )
A B
C D
15.如图甲,点G为BC边的中点,点H在AF上,动点P以每秒2 cm的速度沿路线G→C→D→E→F→H运动,到点H停止,相应的△ABP的面积y(cm2)关于运动时间t(s)的函数图像如图乙所示,若AB=6 cm,则下列结论正确的个数是( )
(第15题)
①图甲中BC长4 cm;
②图甲中DE的长是6 cm;
③图乙中点M表示4s时y值为24 cm2;
④图乙中点N表示12 s时y值为15 cm2.
A.4 B.3 C.2 D.1
16.某市地铁票价计费标准如表所示:
乘车距离x/千米 x≤6 6<x≤12 12<x≤22 22<x≤32 x>32
票价/元 3 4 5 6 每增加
1元可
乘坐20
千米
另外,使用市政交通一卡通,每个自然月每张卡片支出累计满100元后,超出部分打8折;满150元后,超出部分打5折;支出累计达400元后,不再打折.小红妈妈上班时,需要乘坐地铁15千米到达公司,每天上下班共乘坐两次,如果每次乘坐地铁都使用市政交通一卡通,那么每月第21次乘坐地铁上下班时,她刷卡支出的费用是( )
A.2.5元 B.3元 C.4元 D.5元
二、填空题(17题3分,18、19题每题4分,共11分)
17.“五一”期间,小明外出爬山,他从山脚爬到山顶的过程中,中途休息了一段时间.设他从山脚出发后所用时间为t(分钟),所走的路程为s(米),s与t之间的函数关系如图所示.则下列说法中,正确的序号为________.
①小明中途休息用了20分钟;
②小明休息前爬山的平均速度为每分钟70米;
③小明在上述过程中所走的路程为6 600米;
④小明休息前爬山的平均速度大于休息后爬山的平均速度.
(第17题) (第19题)
18.为了加强公民的节水意识,某市制定了如下用水收费标准,每户每月的用水不超过10吨时,水价为每吨2.2元;超过10吨时,超过部分按每吨2.6元收费,若该市某户5月份用水x吨(x>10),应交水费y元,则y关于x的关系式是________________;如果该户居民交了35元水费,那他实际用了________吨水.
19.如图①,点P从△ABC的顶点B出发,沿B→C→A匀速运动到点A停止,图②是点P运动时,线段BP的长度y随时间x变化的关系图像,其中M为曲线部分的最低点,则BC=________,△ABC的面积是________.
三、解答题(20题8分,21~23题每题9分,24、25题每题10分,26题12分,共67分)
20.小红帮弟弟荡秋千,秋千离地面的高度h(m)与摆动时间t(s)之间的关系如图所示.
(1)根据函数的定义,请判断变量h是否是t的函数?
(2)结合图像回答:
①当t=0.7时,h的值是多少?并说明它的实际意义.
②秋千摆动第一个来回需多长时间?
(第20题)
21.星期天,小聪从家里出发到图书馆去看书,再回到家.他离家的距离y(千米)与时间t(分钟)的关系如图所示.
根据图像回答下列问题:
(1)小聪家离图书馆的距离是多少千米?
(2)小聪在图书馆看了多长时间书?
(3)求小聪去图书馆时的速度.
(第21题)
22.有一块10公顷的成熟麦田,用一台收割速度为0.5公顷/时的小麦收割机来收割.
(1)求收割的面积y(公顷)与收割时间x(小时)之间的函数关系式;
(2)求收割完这块麦田需要的时间.
23.弹簧挂上适当的重物后会按一定的规律伸长,已知一弹簧的长度y(cm)与所挂物体的质量x(kg)之间的关系如下表.
所挂物体的质量x/kg 0 1 2 3 4 5 6
弹簧的长度y/cm 15 15.6 16.2 16.8 17.4 18 18.6
(1)表中反映了哪两个变量之间的关系?哪个是自变量?
(2)请直接写出y与x之间的关系式.
(3)当所挂物体的质量逐渐增加(弹簧弹性限度内)时,弹簧的长度怎样变化?
(4)当所挂物体的质量为11.5 kg(弹簧弹性限度内)时,求弹簧的长度.
24.小强利用周日参加了一次社会实践活动,他从果农处以每千克3元的价格购进若干千克草莓到市场上销售,在销售了10千克时,收入50元,余下的每千克降价1元出售.草莓全部售完后,小强共收入70元,请你根据以上信息解答下列问题:
(1)求降价前销售收入y(元)与售出草莓质量x(千克)之间的函数关系式,写出自变量的取值范围,并画出其函数图像.
(2)小强共购进多少千克草莓?小强决定将这次销售草莓获得的利润全部捐给希望工程,那么小强的捐款为多少元?
25.观察下图,然后回答问题.
(1)由上而下第8行,白球有________个,黑球有________个.
(2)若第n行白球与黑球的总数为y个,则y与n的关系式为______________________________________________________________.
(3)请你求出第2 020行白球和黑球的总数.
(第25题)
26.如图①,正方形ABCD的边长为4,点E为AD边的中点,F为AB边上一点,动点P从点B出发,沿B→C→D→E向终点E以每秒a个单位长度的速度运动,设运动时间为t s,△PBF的面积记为S.S与t的部分函数图像如图②所示,已知点M,N(5,6)在S与t的函数图像上.
(1)求线段BF的长及a的值;
(2)写出S与t的函数关系式;
(3)当t为多少时,△PBF的面积S为4?
(第26题)
答案
一、1.C 2.B 3.C 4.B 5.C 6.B
7.C 8.D 9.D 10.A 11.A 12.D
13.C 14.C 15.C 16.C
二、17.①②④
18.y=2.6x-4;15
19.5; 12 点拨:由图像可知点P从B向C运动时,BP长度不断增大,且BP的最大值为5,
即BC=5.
∵图像右端点函数值为5,
∴AB=BC=5.
由于M是曲线部分的最低点,
∴此时BP最小,
即BP⊥AC时,BP=4,
∴由勾股定理可知此时PC=3.
∴AC=2PC=6,
∴△ABC的面积为×4×6=12.
三、20.解:(1)由图可知,对于每一个t的值,h都有唯一确定的值与其对应,
∴变量h是t的函数.
(2)①由函数图像可知,当t=0.7时,h=0.5,它的实际意义是秋千摆动0.7 s时,离地面的高度是0.5 m.
②由图像可知,秋千摆动第一个来回需2.8 s.
21.解:(1)小聪家离图书馆的距离是3千米.
(2)72-12=60(分钟),所以小聪在图书馆看了60分钟书.
(3)3÷12=0.25(千米/分),所以小聪去图书馆时的速度为0.25千米/分.
22.解:(1) 收割的面积y(公顷)与收割时间x(小时)之间的函数关系式为y=0.5x.
(2)把y=10代入y=0.5x中,
得10=0.5x.
解得x=20,即收割完这块麦田需要20小时.
23.解:(1)表中反映了弹簧的长度与所挂物体的质量之间的关系,所挂物体的质量是自变量.
(2)y与x之间的关系式为y=0.6x+15.
(3)当所挂物体的质量逐渐增加(弹簧弹性限度内)时,弹簧的长度逐渐增加.
(4)当所挂物体的质量为11.5 kg时,弹簧的长度为0.6×11.5+15=21.9(cm).
24.解:(1)因为50÷10=5(元/千克),所以y=5x(0≤x≤10),画函数图像略.
(2)设降价后小强售出草莓x千克,由题意,有70-50=(5-1)x,
解得x=5,
所以共购进草莓10+5=15(千克),
所以70-15×3=25(元).
答:小强共购进草莓15千克,小强的捐款为25元.
25.解:(1)8;15
(2)y=3n-1
(3)把n=2 020代入y=3n-1,
得y=6 059.
所以第2 020行白球和黑球的总数为6 059个.
26.解:(1)根据题意可知,当点P在CD上时,△PBF的面积S=6,
则×BF×4=6,解得BF=3.
当t=1时,S=,BP=a,
则×BF×BP=,
即×3a=,
解得a=1,
故线段BF的长为3,a的值为1.
(2)当0<t≤4,即点P在线段BC上运动时,
S=×BF×BP=×3×t=t;
当4<t≤8,即点P在线段CD上运动时,
S=6;
当8<t≤10,即点P在线段DE上运动时,
S=×BF×AP=×3×(12-t)=18-t.
综上可得S与t的函数关系式为
S=
(3)由(2)可得,当0<t≤4时,
t=4,解得t=.
当8解得t=.
故当t=或t=时,△PBF的面积S为4.
一、选择题(1~10题每题3分,11~16题每题2分,共42分)
1.一本笔记本3元,买x本需要y元,在这一问题中,自变量是( )
A.笔记本 B.3 C.x D.y
2.下列表达式中,当x=2时,y=1的是( )
A.y=x+3 B.y=x-1
C.y=x-3 D.y=-x-1
3.下列各图中,不能表示y是x的函数的是( )
4.函数y=-中自变量x的取值范围是( )
A.x≠0 B.x≠1 C.x>1 D.x<1
5.下列说法正确的是( )
A.两个变量间的关系只能用函数表达式表示
B.图像不能直观地反映出函数值随自变量值的变化情况
C.借助表格可以清楚地看出自变量的取值与函数的对应值
D.以上说法都不对
6.邮购一种图书,每册定价36元,另加书价的4%作为邮费,若购书x册,则付款y(元)与购书数量x(册)之间的函数关系式为( )
A.y=36x+4%x B.y=36(1+4%)x
C.y=36.04x D.y=35.96x
7.在某次试验中,测得两个变量x和y之间的4组对应数据如下表:
x 1 2 3 4
y 0 3 8 15
则y与x之间的关系满足的关系式是( )
A.y=2x-2 B.y=3x-3
C.y=x2-1 D.y=x+1
8.电话卡上有4元话费,通话时每分收0.4元话费,则电话卡上的余额y(元)与通话时间t(分)之间的函数图像是( )
A B C D
9.如图是某型号新能源纯电动汽车充满电后,蓄电池剩余电量y(千瓦时)与已行驶路程x(千米)之间的函数图像.下列说法错误的是( )
A.该汽车的蓄电池充满电时,电量是60千瓦时
B.蓄电池剩余电量为35千瓦时时,汽车已行驶了150千米
C.当汽车已行驶180千米时,蓄电池的剩余电量为20千瓦时
D.25千瓦时的电量,汽车能行驶150千米
(第9题) (第12题)
10.函数y=中自变量x的取值范围是( )
A.x<4 B.x≠4 C.x>4 D.x≤4
11.一司机驾驶汽车从甲地去乙地,他以80 km/h的平均速度用2 h到达目的地,当他按原路匀速返回时,汽车的速度v与时间t的函数关系是( )
A.v= B.v= C.v= D.v=
12.某学校组织团员举行“伏羲文化旅游节”宣传活动,从学校骑自行车出发,先上坡到达甲地后,宣传了8分钟,然后下坡到乙地又宣传了8分钟返回,行程情况如图所示.若返回时,上、下坡速度保持不变,在甲地仍要宣传8分钟,那么他们从乙地返回学校所用的时间是( )
A.33分钟 B.46分钟 C.48分钟 D.45.2分钟
13.根据如图所示的程序计算函数y的值,若输入x的值是7,则输出y的值是-2,若输入x的值是-8,则输出y的值是( )
(第13题)
A.5 B.10 C.19 D.21
14.实践证明1分钟跳绳测验的最佳状态是前20秒速度匀速增加,后10秒冲刺,中间速度保持不变,则跳绳速度v(个/秒)与时间t(秒)之间的函数图像大致为( )
A B
C D
15.如图甲,点G为BC边的中点,点H在AF上,动点P以每秒2 cm的速度沿路线G→C→D→E→F→H运动,到点H停止,相应的△ABP的面积y(cm2)关于运动时间t(s)的函数图像如图乙所示,若AB=6 cm,则下列结论正确的个数是( )
(第15题)
①图甲中BC长4 cm;
②图甲中DE的长是6 cm;
③图乙中点M表示4s时y值为24 cm2;
④图乙中点N表示12 s时y值为15 cm2.
A.4 B.3 C.2 D.1
16.某市地铁票价计费标准如表所示:
乘车距离x/千米 x≤6 6<x≤12 12<x≤22 22<x≤32 x>32
票价/元 3 4 5 6 每增加
1元可
乘坐20
千米
另外,使用市政交通一卡通,每个自然月每张卡片支出累计满100元后,超出部分打8折;满150元后,超出部分打5折;支出累计达400元后,不再打折.小红妈妈上班时,需要乘坐地铁15千米到达公司,每天上下班共乘坐两次,如果每次乘坐地铁都使用市政交通一卡通,那么每月第21次乘坐地铁上下班时,她刷卡支出的费用是( )
A.2.5元 B.3元 C.4元 D.5元
二、填空题(17题3分,18、19题每题4分,共11分)
17.“五一”期间,小明外出爬山,他从山脚爬到山顶的过程中,中途休息了一段时间.设他从山脚出发后所用时间为t(分钟),所走的路程为s(米),s与t之间的函数关系如图所示.则下列说法中,正确的序号为________.
①小明中途休息用了20分钟;
②小明休息前爬山的平均速度为每分钟70米;
③小明在上述过程中所走的路程为6 600米;
④小明休息前爬山的平均速度大于休息后爬山的平均速度.
(第17题) (第19题)
18.为了加强公民的节水意识,某市制定了如下用水收费标准,每户每月的用水不超过10吨时,水价为每吨2.2元;超过10吨时,超过部分按每吨2.6元收费,若该市某户5月份用水x吨(x>10),应交水费y元,则y关于x的关系式是________________;如果该户居民交了35元水费,那他实际用了________吨水.
19.如图①,点P从△ABC的顶点B出发,沿B→C→A匀速运动到点A停止,图②是点P运动时,线段BP的长度y随时间x变化的关系图像,其中M为曲线部分的最低点,则BC=________,△ABC的面积是________.
三、解答题(20题8分,21~23题每题9分,24、25题每题10分,26题12分,共67分)
20.小红帮弟弟荡秋千,秋千离地面的高度h(m)与摆动时间t(s)之间的关系如图所示.
(1)根据函数的定义,请判断变量h是否是t的函数?
(2)结合图像回答:
①当t=0.7时,h的值是多少?并说明它的实际意义.
②秋千摆动第一个来回需多长时间?
(第20题)
21.星期天,小聪从家里出发到图书馆去看书,再回到家.他离家的距离y(千米)与时间t(分钟)的关系如图所示.
根据图像回答下列问题:
(1)小聪家离图书馆的距离是多少千米?
(2)小聪在图书馆看了多长时间书?
(3)求小聪去图书馆时的速度.
(第21题)
22.有一块10公顷的成熟麦田,用一台收割速度为0.5公顷/时的小麦收割机来收割.
(1)求收割的面积y(公顷)与收割时间x(小时)之间的函数关系式;
(2)求收割完这块麦田需要的时间.
23.弹簧挂上适当的重物后会按一定的规律伸长,已知一弹簧的长度y(cm)与所挂物体的质量x(kg)之间的关系如下表.
所挂物体的质量x/kg 0 1 2 3 4 5 6
弹簧的长度y/cm 15 15.6 16.2 16.8 17.4 18 18.6
(1)表中反映了哪两个变量之间的关系?哪个是自变量?
(2)请直接写出y与x之间的关系式.
(3)当所挂物体的质量逐渐增加(弹簧弹性限度内)时,弹簧的长度怎样变化?
(4)当所挂物体的质量为11.5 kg(弹簧弹性限度内)时,求弹簧的长度.
24.小强利用周日参加了一次社会实践活动,他从果农处以每千克3元的价格购进若干千克草莓到市场上销售,在销售了10千克时,收入50元,余下的每千克降价1元出售.草莓全部售完后,小强共收入70元,请你根据以上信息解答下列问题:
(1)求降价前销售收入y(元)与售出草莓质量x(千克)之间的函数关系式,写出自变量的取值范围,并画出其函数图像.
(2)小强共购进多少千克草莓?小强决定将这次销售草莓获得的利润全部捐给希望工程,那么小强的捐款为多少元?
25.观察下图,然后回答问题.
(1)由上而下第8行,白球有________个,黑球有________个.
(2)若第n行白球与黑球的总数为y个,则y与n的关系式为______________________________________________________________.
(3)请你求出第2 020行白球和黑球的总数.
(第25题)
26.如图①,正方形ABCD的边长为4,点E为AD边的中点,F为AB边上一点,动点P从点B出发,沿B→C→D→E向终点E以每秒a个单位长度的速度运动,设运动时间为t s,△PBF的面积记为S.S与t的部分函数图像如图②所示,已知点M,N(5,6)在S与t的函数图像上.
(1)求线段BF的长及a的值;
(2)写出S与t的函数关系式;
(3)当t为多少时,△PBF的面积S为4?
(第26题)
答案
一、1.C 2.B 3.C 4.B 5.C 6.B
7.C 8.D 9.D 10.A 11.A 12.D
13.C 14.C 15.C 16.C
二、17.①②④
18.y=2.6x-4;15
19.5; 12 点拨:由图像可知点P从B向C运动时,BP长度不断增大,且BP的最大值为5,
即BC=5.
∵图像右端点函数值为5,
∴AB=BC=5.
由于M是曲线部分的最低点,
∴此时BP最小,
即BP⊥AC时,BP=4,
∴由勾股定理可知此时PC=3.
∴AC=2PC=6,
∴△ABC的面积为×4×6=12.
三、20.解:(1)由图可知,对于每一个t的值,h都有唯一确定的值与其对应,
∴变量h是t的函数.
(2)①由函数图像可知,当t=0.7时,h=0.5,它的实际意义是秋千摆动0.7 s时,离地面的高度是0.5 m.
②由图像可知,秋千摆动第一个来回需2.8 s.
21.解:(1)小聪家离图书馆的距离是3千米.
(2)72-12=60(分钟),所以小聪在图书馆看了60分钟书.
(3)3÷12=0.25(千米/分),所以小聪去图书馆时的速度为0.25千米/分.
22.解:(1) 收割的面积y(公顷)与收割时间x(小时)之间的函数关系式为y=0.5x.
(2)把y=10代入y=0.5x中,
得10=0.5x.
解得x=20,即收割完这块麦田需要20小时.
23.解:(1)表中反映了弹簧的长度与所挂物体的质量之间的关系,所挂物体的质量是自变量.
(2)y与x之间的关系式为y=0.6x+15.
(3)当所挂物体的质量逐渐增加(弹簧弹性限度内)时,弹簧的长度逐渐增加.
(4)当所挂物体的质量为11.5 kg时,弹簧的长度为0.6×11.5+15=21.9(cm).
24.解:(1)因为50÷10=5(元/千克),所以y=5x(0≤x≤10),画函数图像略.
(2)设降价后小强售出草莓x千克,由题意,有70-50=(5-1)x,
解得x=5,
所以共购进草莓10+5=15(千克),
所以70-15×3=25(元).
答:小强共购进草莓15千克,小强的捐款为25元.
25.解:(1)8;15
(2)y=3n-1
(3)把n=2 020代入y=3n-1,
得y=6 059.
所以第2 020行白球和黑球的总数为6 059个.
26.解:(1)根据题意可知,当点P在CD上时,△PBF的面积S=6,
则×BF×4=6,解得BF=3.
当t=1时,S=,BP=a,
则×BF×BP=,
即×3a=,
解得a=1,
故线段BF的长为3,a的值为1.
(2)当0<t≤4,即点P在线段BC上运动时,
S=×BF×BP=×3×t=t;
当4<t≤8,即点P在线段CD上运动时,
S=6;
当8<t≤10,即点P在线段DE上运动时,
S=×BF×AP=×3×(12-t)=18-t.
综上可得S与t的函数关系式为
S=
(3)由(2)可得,当0<t≤4时,
t=4,解得t=.
当8
故当t=或t=时,△PBF的面积S为4.
同课章节目录
- 第十八章 数据的收集与整理
- 18.1 统计的初步认识
- 18.2 抽样调查
- 18.3 数据的整理与表示
- 18.4 频数分布表与直方图
- 第十九章 平面直角坐标系
- 19.1 确定平面上物体的位置
- 19.2 平面直角坐标系
- 19.3 坐标与图形的位置
- 19.4 坐标与图形的变化
- 第二十章 函数
- 20.1 常量和变量
- 20.2 函数
- 20.3 函数的表示
- 20.4 函数的初步应用
- 第二十一章 一次函数
- 21.1 一次函数
- 21.2 一次函数的图像和性质
- 21.3 用待定系数法确定一次函数表达式
- 21.4 一次函数的应用
- 21.5 一次函数与二元一次方程的关系
- 第二十二章 四边形
- 22.1 平行四边形的性质
- 22.2 平行四边形的判断
- 22.3 三角形的中位线
- 22.4 矩形
- 22.5 菱形
- 22.6 正方形
- 22.7 多边形的内角和与外角和
