九年级数学弧弦圆心角

24.1.3弧、弦、圆心角
(Arc / chord / centralangle)
I【教学内容 】
1.圆心角的概念.
2.弧、弦、圆心角的关系定理和定理的应用.
定理：“在同圆或等圆中，相等的圆心角所对的所对的弧相等，所对的弦也相等” .
3.弧、弦、圆心角的关系定理的推论及其应用.
（1）推论1：在同圆或等圆中，相等的弧所对的所对圆心角的相等，所对的弦也相等.
（2）推论2：在同圆或等圆中，相等的弦所对的所对的圆心角相等，所对的弧也相等.
II【教学目标】
1知识与技能
1.1了解圆心角的概念.
1.2掌握弧、弦、圆心角的关系定理：
“在同圆或等圆中，两个圆心角、弧、弦中有一组量相等，它们所对的其余各组量也相等”.
1.3会最后利用弧、弦、圆心角的关系定理解决一些具体问题.
1.4通过旋转变换，使学生明确图形在变化过程中的特点和规律，并进一步发展学生的观察能力和空间想象力.
2.过程与方法
2.1教学过程中鼓励学生动手、动口、动脑。并进行同伴之间的交流.
2.2通过复习旋转的知识，产生圆心角的概念，然后用圆心角和旋转的知识探索弧、弦、圆心角的关系定理：“在同圆或等圆中，两个圆心角、弧、弦中有一组量相等，它们所对的其余各组量也相等”。最后利用它们解决一些具体问题.
2.3 经历观察、分析、证明、归纳的过程，发展学生的数学思考能力和推理能力.
3.情感态度和价值观
3.1经历探索弧、弦、圆心角的关系定理及推论的过程，发展学生的数学思考能力和推理能力.
3.2通过积极引导，帮助学生有意识地积累活动经验，获得成功的体验.
3.3利用现实生活和数学中的素材，设计具有挑战性的情景，激发学生求知和探索的欲望.
III【教学重点】
1.弧、弦、圆心角的关系定理：
“在同圆或等圆中，两个圆心角、弧、弦中有一组量相等，它们所对的其余各组量也相等”.
2.定理的两个推论及其在解题中的应用.
IV【教学难点】
弧、弦、圆心角的关系定理的探索、推导和应用.
V【教学过程】
A.引入新课
1.复习引入：
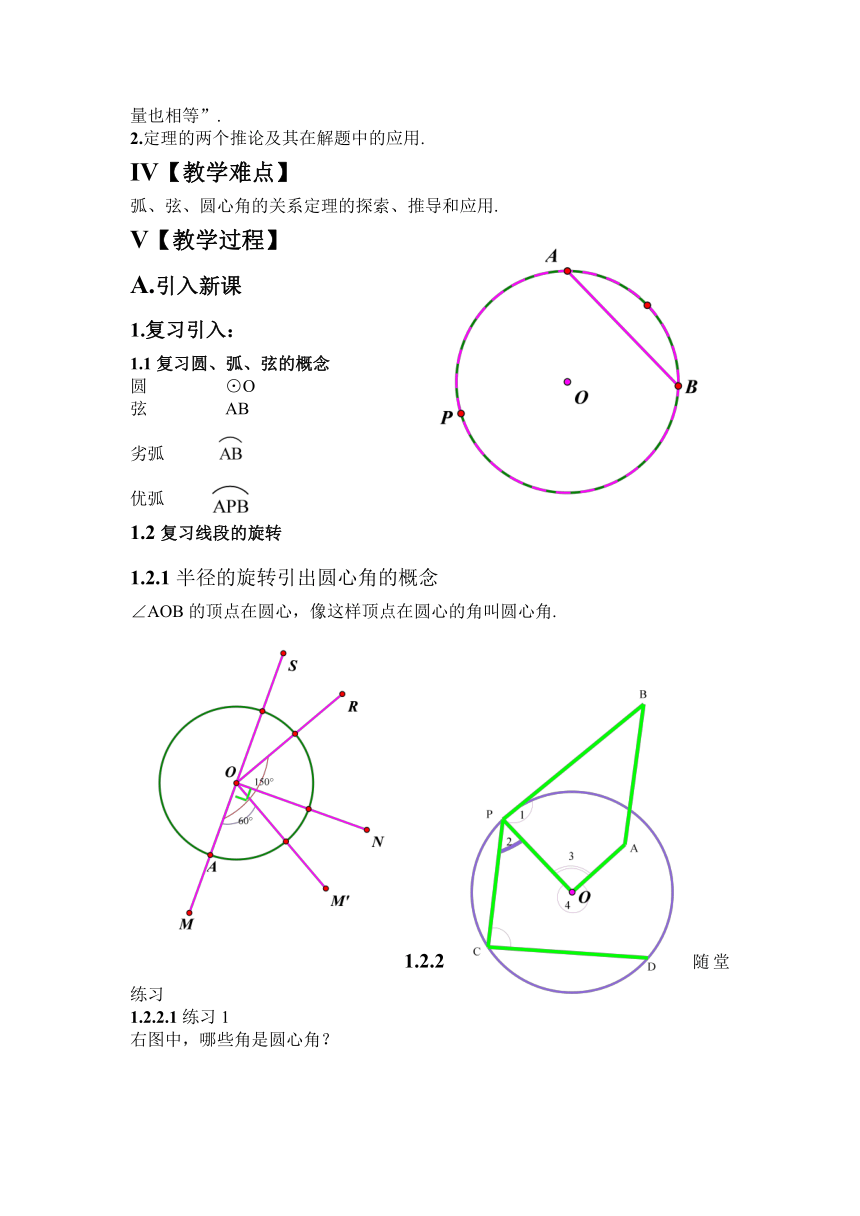
1.1复习圆、弧、弦的概念
圆 ⊙O
弦 AB
劣弧
优弧
1.2复习线段的旋转
1.2.1半径的旋转引出圆心角的概念
∠AOB的顶点在圆心，像这样顶点在圆心的角叫圆心角.
1.2.2随堂练习
1.2.2.1练习1
右图中，哪些角是圆心角？
1.2.2.2练习2
（1）∠AOB所对的弦是（ ），所对的弧是 （ ）
（2） 所对的弦是（ ），所对的圆心角是（ ）
（3）弦AB所对的圆心角
是（ ），所对的弧是（ ）
1.3提出问题
猜一猜
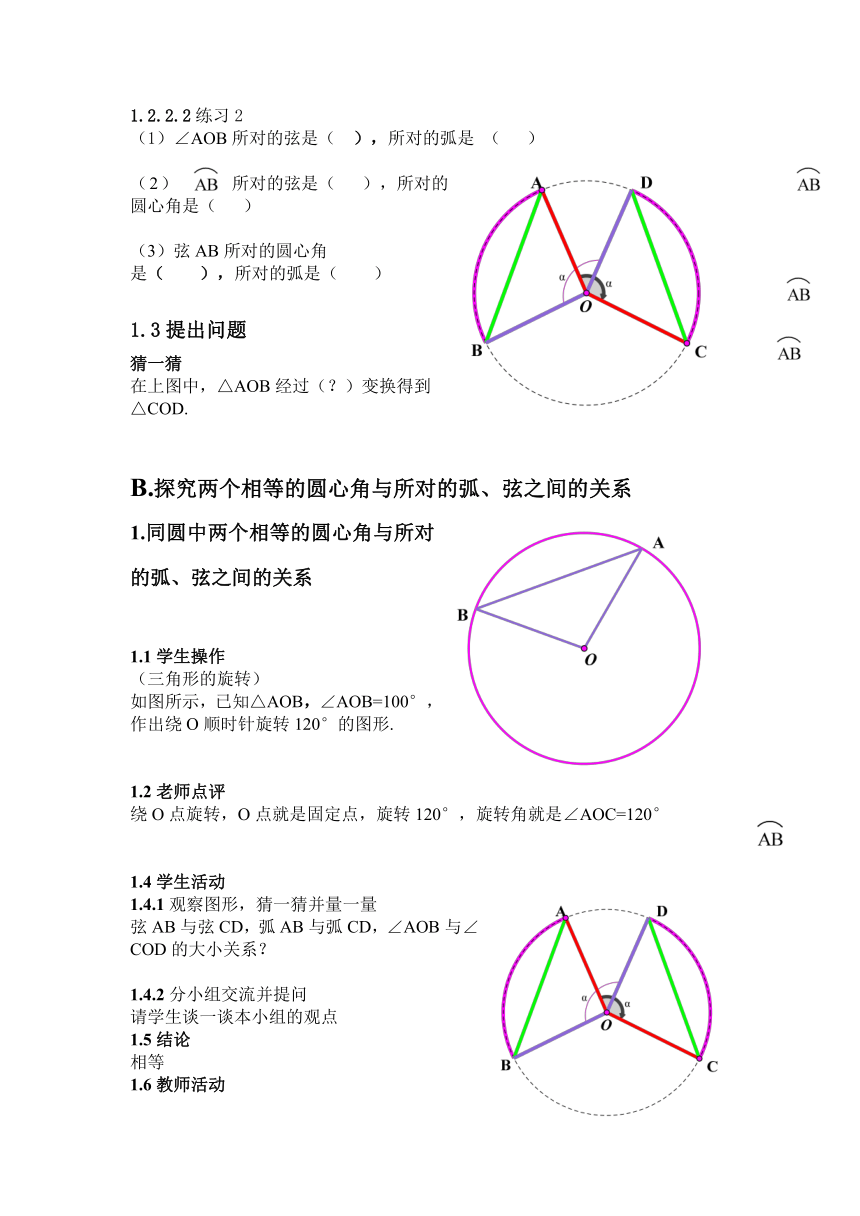
在上图中，△AOB经过（？）变换得到
△COD.
B.探究两个相等的圆心角与所对的弧、弦之间的关系
1.同圆中两个相等的圆心角与所对的弧、弦之间的关系
1.1学生操作
（三角形的旋转）
如图所示，已知△AOB，∠AOB=100°，作出绕O顺时针旋转120°的图形.
1.2老师点评
绕O点旋转，O点就是固定点，旋转120°，旋转角就是∠AOC=120°
1.4学生活动
1.4.1观察图形，猜一猜并量一量
弦AB与弦CD，弧AB与弧CD，∠AOB与∠COD的大小关系？
1.4.2分小组交流并提问
请学生谈一谈本小组的观点
1.5结论
相等
1.6教师活动
1.6.1几何画板展示图形的旋转
拖动点A旋转△AOB，使
△AOB与△COD重合
1.6.2学生观察思考获得结论
相等
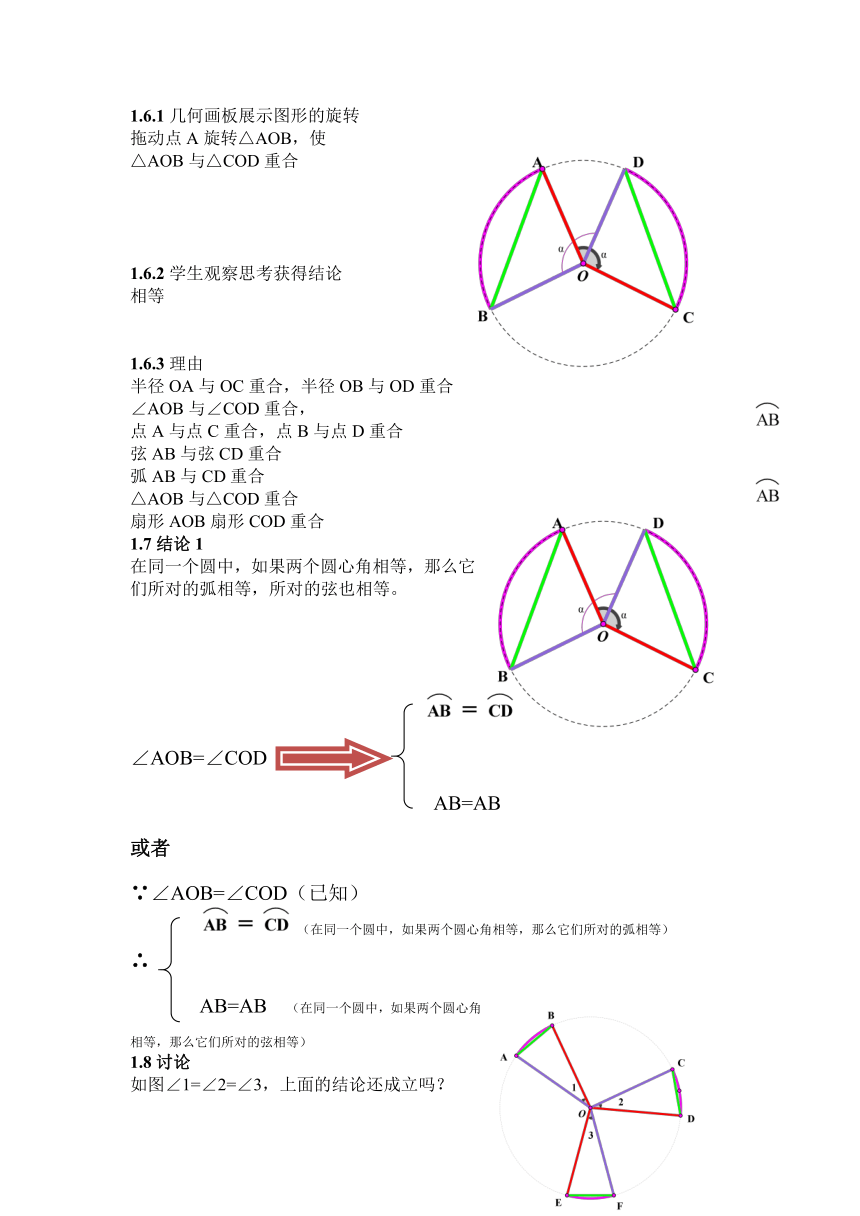
1.6.3理由
半径OA与OC重合，半径OB与OD重合
∠AOB与∠COD重合，
点A与点C重合，点B与点D重合
弦AB与弦CD重合
弧AB与CD重合
△AOB与△COD重合
扇形AOB扇形COD重合
1.7结论1
在同一个圆中，如果两个圆心角相等，那么它们所对的弧相等，所对的弦也相等。
∠AOB=∠COD
AB=AB
或者
∵∠AOB=∠COD（已知）
（在同一个圆中，如果两个圆心角相等，那么它们所对的弧相等）
∴
AB=AB （在同一个圆中，如果两个圆心角相等，那么它们所对的弦相等）
1.8讨论
如图∠1=∠2=∠3，上面的结论还成立吗？
AB=CD=EF
∠1=∠2=∠3
1.9定理1：
在同一个圆中，相等的圆心角所对的弧相等，所对的弦也相等.
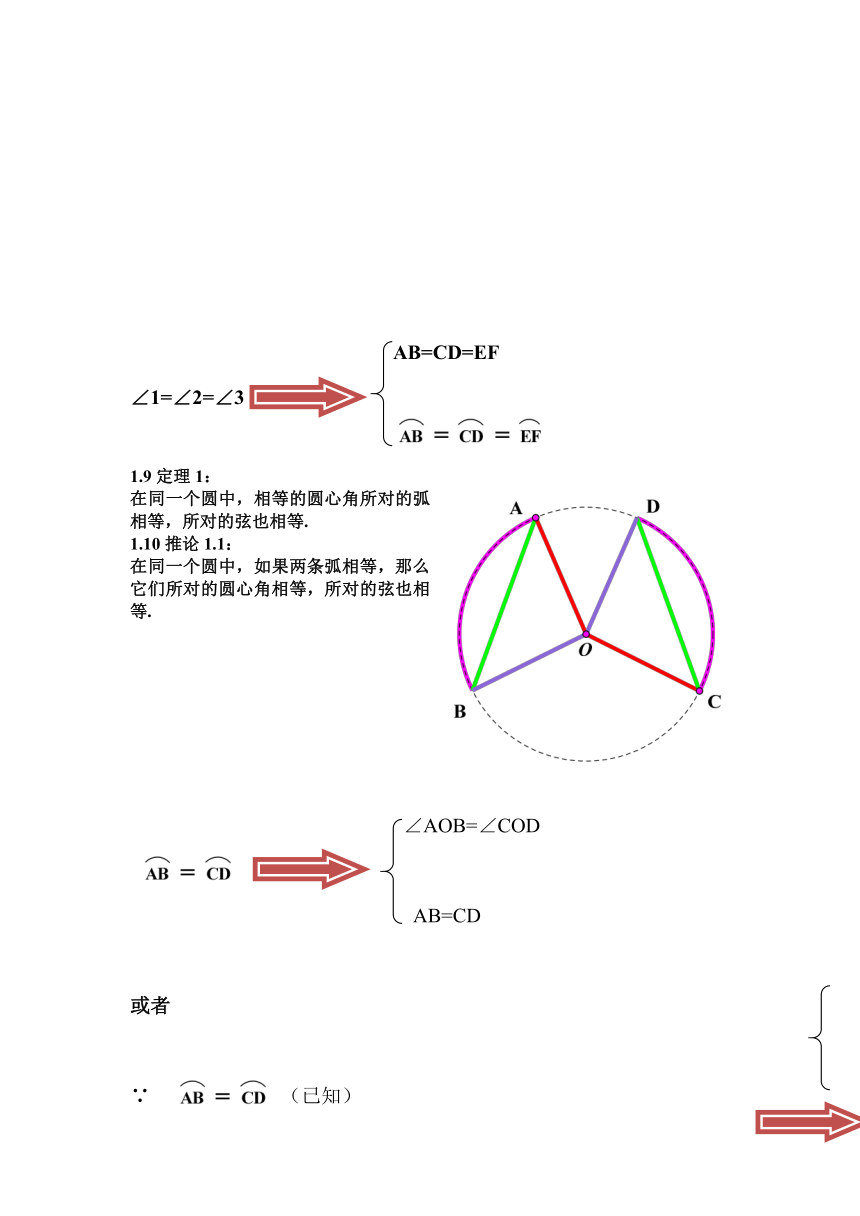
1.10推论1.1：
在同一个圆中，如果两条弧相等，那么它们所对的圆心角相等，所对的弦也相等.
∠AOB=∠COD
AB=CD
或者
∵ （已知）
∠AOB=∠COD（在同一个圆中，如果两条弧相等，那么它们所对的圆心角相等）
∴
AB=CD （在同一个圆中，如果两条弧相等，那么它们所对的弦相等）
1.11推论1.2：
在同一个圆中，如果两条弦相等，那么它们所对的圆心角相等，所对的弧也相等.
∠OB=∠CODA
AB=CD
或者
∵ AB=CD（已知）
∠AOB=∠COD（在同一个圆中，如果两条弦相等，那么它们所对的圆心角相等）
∴
（在同一个圆中，如果两条弦相等，那么它们所对的弧相等）
2探究等圆中两个相等的圆心角与所对的弧弦的关系
2.1提出问题
在两个等圆中，相等的圆心角所对的弧相等吗？所对的弦也相等吗？
请同学们现在动手作一作.
2.2学生活动
如图1，在⊙O和⊙Y中，分别作相等的圆心角∠AOB与∠CYD，得如图2，平移⊙O，使O 与Y重合，固定圆心，将⊙O旋转一个角度，使得OA与YC重合，你能发现那些等量关系，说一说你的理由？
我能发现：AB=CD，
2.3老师活动
2.3.1老师用几何画板演示在⊙O和⊙Y中的运动、旋转、重合过程，学生观察思考
2.3.2老师点评
现在，它的证明方法就化为前面的说明了，这就是又回到了我们的数学思想方法------化归思想。化未知为已知.
2.4定理2
因此，我们得到下面的定理：
定理2：在等圆中，如果两个圆心角相等，那么它们所对的弧相等，所对的弦也相等.
∠AOB=∠COD
AB=AB
或者
∵∠AOB=∠COD（已知）
（在等圆中，如果两个圆心角相等，那么它们所对的弧相等）
∴
AB=AB（在等圆圆中，如果两个圆心角相等，那么它们所对的弦相等）
2.5推论2-1
在等圆中，如果两条弧相等，那么它们所对的圆心角相等，所对的弦也相等.
∠AOB=∠CYD
AB=CD
或者
∵ （已知）
∠AOB=∠CYD（在等圆中，如果两条弧相等，那么它们所对的圆心角相等）
∴
AB=CD （在等圆中，如果两条弧相等，那么它们所对的弦相等）
2.6推论2-2
在等圆中，如果两条弦相等，那么它们所对的圆心角相等，所对的弧也相等.
∠AOB=∠CYD
AB=CD
或者
∵ AB=CD（已知）
∠AOB=∠COD（在等圆中，如果两条弦相等，那么它们所对的圆心角相等）
∴
（在等圆中，如果两条弦相等，那么它们所对的弧相等）
3归纳
3.1请同学们用3句话归纳上面的2个定理和4个推论：
3.2教材P83（请同学们看书）
3.3圆心角、弧、弦的关系定理：
在同圆或等圆中，如果两个圆心角相等，那么它们所对的弧相等，所对的弦也相等.
3.4推论1：
在同圆或等圆中，如果两条弧相等，那么它们所对的所对圆心角的相等，所对的弦也相等.
3.5推论2：
在同圆或等圆中，如果两条弦相等，那么它们所对的所对的圆心角相等，所对的弧也相等。
3.6请同学们把教材P83的1个定理和2个推论用1个定理描述：
弧、弦、圆心角的关系定理：
在同圆或等圆中，两个圆心角、弧、弦中有一组量相等，它们所对的其余各组量也相等.
C知识应用
例题1
如图，在⊙O中，AB与CD是两条弦，OE⊥AB，OF⊥CD，垂足分别是E、F.
如果∠AOB与∠COD，求证OE=OF.
如果OE=OF，求证AB=CD，弧AB=CD，∠AOB与∠COD.
2.巩固练习
教材P89练习1，教材P90练习2.
3.例2
如图，在⊙O中， ，
∠ACB=60°，
求证∠AOB=∠AOC=∠BOC.
3.1方法1
3.1.1分析法探索解题方法
3.1.2综合法书写证明过程
证明：
∵ （已知）
∴AB=AC（同圆中相等的弧所对的弦相等）
∴△ABC是等腰三角形（等腰三角形的定义）
∵∠ACB=60°（已知）
∴△ABC是等边三角形（有一个角是60°的等腰三角形是等边三角形）
∴AB=AC=BC（等边三角形的定义）
∴∠AOB=∠AOC=∠BOC（同圆中相等的弦所对的圆心角相等）
3.2方法2
分析：证△AOC△BOC，再证∠ACO=∠BCO=30°，,∠AOC=∠BOC=120°
D.课堂小结
本节课应掌握
1圆心角的概念.
2弧、弦、圆心角的关系定理：
在同圆或等圆中，两个圆心角、弧、弦中有一组量相等，它们所对的其余各组量也相等。
3利用弧、弦、圆心角的关系定理解决一些具体问题.
VI【课外作业】
1布置作业.
1.1教材P87，复习巩固2，3，教材P88，综合应用11.
1.2 课外作业辅导、批改、反馈信息、改错反思.
2选用课时作业设计
VII【课后反思】