1.1.3 四种命题间的相互关系
文档属性
| 名称 | 1.1.3 四种命题间的相互关系 |  | |
| 格式 | rar | ||
| 文件大小 | 76.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-10-21 19:19:16 | ||
图片预览






文档简介
(共20张PPT)
授课班级:高二(7)班
1、命题:一般地,在数学中用语言、符号或式子表
达的,可以判断真假的陈述句叫做命题。
其中,判断为真的语句叫做真命题,
判断为假的语句叫做假命题。
2、命题的形式:
“若p,则q”
其中,p叫做命题的条件,q叫做命题的结论。
复 习
交换原命题的条件和结论,所得的命题是原命题的 ________
同时否定原命题的条件和结论,所得的命题是原命题的________
交换原命题的条件和结论,并且同时否定,所得的命题是 原命题的__________
逆命题。
否命题。
逆否命题。
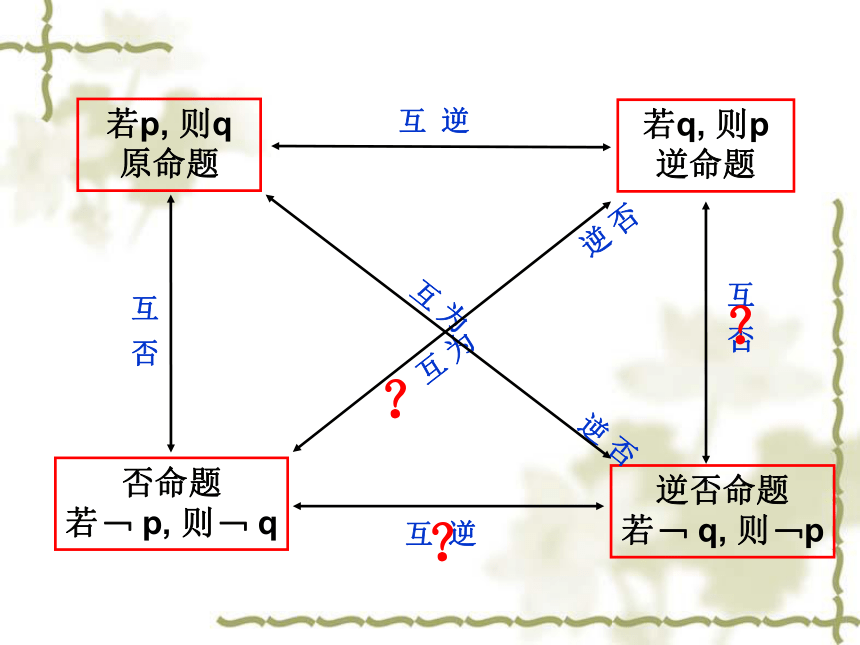
3、四种命题:原命题
逆命题
否命题
逆否命题
若 p,则 q
若 q,则 p
若﹁ p, 则﹁ q
若﹁ q, 则﹁ p
若p, 则q
原命题
若q, 则p
逆命题
否命题
若﹁ p, 则﹁ q
逆否命题
若﹁ q, 则﹁p
互 为 逆 否
互 为 逆 否
互 逆
互 逆
互 否
互 否
?
?
?
原命题:若 a>b, 则 a+c>b+c .
逆命题:
逆否命题:
否命题:
若 a+c>b+c,则 a>b.
若 a≤b,则 a+c≤b+c.
若 a+c≤b+c,则 a≤b.
练习:分别写出下列命题的逆命题、否命题、逆否
命题,并判断它们的真假。
(真)
(真)
(真)
(真)
四种命题之间的真假性是否有一定的相互关系?
问题 1——互为逆命题的两个命题间的真假关系
①原命题:若 a>b,则 a+c>b+c。
逆命题:若 a+c>b+c,则 a>b。
②原命题:若四边形是正方形,则四边形的两对角线互相垂直。
逆命题:若四边形的两对角线互相垂直,则四边形是正方形。
③原命题:若 a>b,则 ac2>bc2。
逆命题:若 ac2>bc2,则 a>b。
④原命题:若四边形的对角线相等,则四边形是平行四边形。
逆命题:若四边形是平行四边形,则四边形的对角线相等。
真
真
真
假
假
真
假
假
1、写出下列命题的逆命题,并判断命题的真假。
结 论 1
原命题的真假和逆命题的真假没有关系。
也就是说,两个命题为互逆命题,它们的真假性没有关系。
问题 2——互为否命题的两个命题间的真假关系
①原命题:若 a>b,则 a+c>b+c。
②原命题:若四边形是正方形,则四边形两对角线互相垂直。
③原命题:若 a>b,则 ac2>bc2。
④原命题:若四边形的对角线相等,则四边形是平行四边形。
真
真
真
假
假
真
假
假
2、写出下列命题的否命题,并判断命题的真假。
否命题:若a≤b,则 a+c≤b+c。
否命题:若四边形不是正方形,则四边形两对角线互相不垂直。
否命题:若a≤b,则 ac2≤bc2。
否命题:若四边形对角线不相等,则四边形不是平行四边形。
结 论 2
原命题的真假和否命题的真假没有关系。
也就是说,两个命题为互否命题,它们的真假性没有关系。
问题 3——互为逆否命题的两个命题间的真假关系
①原命题:若 a>b,则 a+c>b+c。
②原命题:若四边形是正方形,则四边形两对角线互相垂直。
③原命题:若 a>b,则 ac2>bc2。
④原命题:若四边形的对角线相等,则四边形是平行四边形。
真
真
真
真
假
假
假
假
3、 写出下列命题的逆否命题,并判断命题的真假。
逆否命题:若 a+c≤b+c,则 a≤b。
逆否命题:若四边形两对角线互相不垂直,则四边形不是正方形。
逆否命题:若 ac2≤bc2,则 a≤b。
逆否命题:若四边形不是平行四边形,则四边形的对角线不相等。
结 论 3
原命题和逆否命题同真同假。 也就是说, 两个命题互为逆否命题,它们的真假性相同。
四种命题的真假性之间的关系如下:
1、两个命题互为逆否命题,它们的真假性相同;
2、两个命题为互逆命题或互否命题,它们的真假性没有关系。
四种命题的真假性,有且只有下面四种情况:
原命题
逆命题
否命题
逆否命题
真
真
真
真
真
真
真
真
假
假
假
假
假
假
假
假
例1:以“若x -3x+2=0,则x=2”为原命题,写出它的
逆命题、否命题与逆否命题,并判断真假。
逆命题:若x=2,则x -3x+2=0.
否命题:若x -3x+2≠0,则x≠2.
逆否命题:若x≠2,则x -3x+2≠0.
(真)
(真)
(假)
分析:原命题的条件p:x -3x+2=0,结论q:x=2.
找出原命题的
条件p和结论q
按照四种命题的
结构写出所以命题
判断真假
(互为逆否命题的两个命题真假性相同)
解: 原命题:若x -3x+2=0,则x=2.
(假)
练习:写出命题“若x>5,则x>0”的逆命题、否命题
与逆否命题,并判断真假。
分析:原命题的条件p:x>5,结论q:x>0.
逆命题:若x>0, 则x>5.
否命题:若x≤5,则x≤0.
逆否命题:若x≤0,则x≤5.
(假)
(假)
(真)
解:原命题:若x>5, 则x>0.
(真)
例2:证明:若x +y =0,则x=y=0.
分析:在判断一个命题的真假有困难时,我们可以判断其
等价命题——逆否命题的真假。因为互为逆否命题
的两个命题真假性相同。
解:原命题的逆否命题:
“若x,y中至少有一个不为0,则x +y ≠0”.
因此,不妨设 x≠0,则 x >0,
所以 x +y >0,
原命题的逆否命题是真命题,原命题也为真命题。
即 x +y ≠0.
P8 证明:若a -b +2a-4b-3≠0,则a-b≠1.
练 习
证明:原命题的逆否命题是:
“若a-b=1 ,则a -b +2a-4b-3=0”.
∵ a-b=1,
∴ a -b +2a-4b-3=(a+b)(a-b)+2a-4b-3
=a+b+2a-4b-3
=3a-3b-3
=3(a-b)-3
=0
所以,原命题的逆否命题是真命题,原命题也为真命题。
课堂小结
若p, 则q
原命题
若q, 则p
逆命题
否命题
若﹁ p, 则﹁ q
逆否命题
若﹁ q, 则﹁p
互为逆否
互为逆否
互逆
互 否
真假无关
真假无关
互逆
真假无关
互 否
真假无关
同真同假
同真同假
作业:P8 A组
T 3、4
授课班级:高二(7)班
1、命题:一般地,在数学中用语言、符号或式子表
达的,可以判断真假的陈述句叫做命题。
其中,判断为真的语句叫做真命题,
判断为假的语句叫做假命题。
2、命题的形式:
“若p,则q”
其中,p叫做命题的条件,q叫做命题的结论。
复 习
交换原命题的条件和结论,所得的命题是原命题的 ________
同时否定原命题的条件和结论,所得的命题是原命题的________
交换原命题的条件和结论,并且同时否定,所得的命题是 原命题的__________
逆命题。
否命题。
逆否命题。
3、四种命题:原命题
逆命题
否命题
逆否命题
若 p,则 q
若 q,则 p
若﹁ p, 则﹁ q
若﹁ q, 则﹁ p
若p, 则q
原命题
若q, 则p
逆命题
否命题
若﹁ p, 则﹁ q
逆否命题
若﹁ q, 则﹁p
互 为 逆 否
互 为 逆 否
互 逆
互 逆
互 否
互 否
?
?
?
原命题:若 a>b, 则 a+c>b+c .
逆命题:
逆否命题:
否命题:
若 a+c>b+c,则 a>b.
若 a≤b,则 a+c≤b+c.
若 a+c≤b+c,则 a≤b.
练习:分别写出下列命题的逆命题、否命题、逆否
命题,并判断它们的真假。
(真)
(真)
(真)
(真)
四种命题之间的真假性是否有一定的相互关系?
问题 1——互为逆命题的两个命题间的真假关系
①原命题:若 a>b,则 a+c>b+c。
逆命题:若 a+c>b+c,则 a>b。
②原命题:若四边形是正方形,则四边形的两对角线互相垂直。
逆命题:若四边形的两对角线互相垂直,则四边形是正方形。
③原命题:若 a>b,则 ac2>bc2。
逆命题:若 ac2>bc2,则 a>b。
④原命题:若四边形的对角线相等,则四边形是平行四边形。
逆命题:若四边形是平行四边形,则四边形的对角线相等。
真
真
真
假
假
真
假
假
1、写出下列命题的逆命题,并判断命题的真假。
结 论 1
原命题的真假和逆命题的真假没有关系。
也就是说,两个命题为互逆命题,它们的真假性没有关系。
问题 2——互为否命题的两个命题间的真假关系
①原命题:若 a>b,则 a+c>b+c。
②原命题:若四边形是正方形,则四边形两对角线互相垂直。
③原命题:若 a>b,则 ac2>bc2。
④原命题:若四边形的对角线相等,则四边形是平行四边形。
真
真
真
假
假
真
假
假
2、写出下列命题的否命题,并判断命题的真假。
否命题:若a≤b,则 a+c≤b+c。
否命题:若四边形不是正方形,则四边形两对角线互相不垂直。
否命题:若a≤b,则 ac2≤bc2。
否命题:若四边形对角线不相等,则四边形不是平行四边形。
结 论 2
原命题的真假和否命题的真假没有关系。
也就是说,两个命题为互否命题,它们的真假性没有关系。
问题 3——互为逆否命题的两个命题间的真假关系
①原命题:若 a>b,则 a+c>b+c。
②原命题:若四边形是正方形,则四边形两对角线互相垂直。
③原命题:若 a>b,则 ac2>bc2。
④原命题:若四边形的对角线相等,则四边形是平行四边形。
真
真
真
真
假
假
假
假
3、 写出下列命题的逆否命题,并判断命题的真假。
逆否命题:若 a+c≤b+c,则 a≤b。
逆否命题:若四边形两对角线互相不垂直,则四边形不是正方形。
逆否命题:若 ac2≤bc2,则 a≤b。
逆否命题:若四边形不是平行四边形,则四边形的对角线不相等。
结 论 3
原命题和逆否命题同真同假。 也就是说, 两个命题互为逆否命题,它们的真假性相同。
四种命题的真假性之间的关系如下:
1、两个命题互为逆否命题,它们的真假性相同;
2、两个命题为互逆命题或互否命题,它们的真假性没有关系。
四种命题的真假性,有且只有下面四种情况:
原命题
逆命题
否命题
逆否命题
真
真
真
真
真
真
真
真
假
假
假
假
假
假
假
假
例1:以“若x -3x+2=0,则x=2”为原命题,写出它的
逆命题、否命题与逆否命题,并判断真假。
逆命题:若x=2,则x -3x+2=0.
否命题:若x -3x+2≠0,则x≠2.
逆否命题:若x≠2,则x -3x+2≠0.
(真)
(真)
(假)
分析:原命题的条件p:x -3x+2=0,结论q:x=2.
找出原命题的
条件p和结论q
按照四种命题的
结构写出所以命题
判断真假
(互为逆否命题的两个命题真假性相同)
解: 原命题:若x -3x+2=0,则x=2.
(假)
练习:写出命题“若x>5,则x>0”的逆命题、否命题
与逆否命题,并判断真假。
分析:原命题的条件p:x>5,结论q:x>0.
逆命题:若x>0, 则x>5.
否命题:若x≤5,则x≤0.
逆否命题:若x≤0,则x≤5.
(假)
(假)
(真)
解:原命题:若x>5, 则x>0.
(真)
例2:证明:若x +y =0,则x=y=0.
分析:在判断一个命题的真假有困难时,我们可以判断其
等价命题——逆否命题的真假。因为互为逆否命题
的两个命题真假性相同。
解:原命题的逆否命题:
“若x,y中至少有一个不为0,则x +y ≠0”.
因此,不妨设 x≠0,则 x >0,
所以 x +y >0,
原命题的逆否命题是真命题,原命题也为真命题。
即 x +y ≠0.
P8 证明:若a -b +2a-4b-3≠0,则a-b≠1.
练 习
证明:原命题的逆否命题是:
“若a-b=1 ,则a -b +2a-4b-3=0”.
∵ a-b=1,
∴ a -b +2a-4b-3=(a+b)(a-b)+2a-4b-3
=a+b+2a-4b-3
=3a-3b-3
=3(a-b)-3
=0
所以,原命题的逆否命题是真命题,原命题也为真命题。
课堂小结
若p, 则q
原命题
若q, 则p
逆命题
否命题
若﹁ p, 则﹁ q
逆否命题
若﹁ q, 则﹁p
互为逆否
互为逆否
互逆
互 否
真假无关
真假无关
互逆
真假无关
互 否
真假无关
同真同假
同真同假
作业:P8 A组
T 3、4
