24.1.3弧、弦、圆心角
文档属性
| 名称 | 24.1.3弧、弦、圆心角 |

|
|
| 格式 | rar | ||
| 文件大小 | 657.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-10-21 00:00:00 | ||
图片预览


文档简介
(共25张PPT)
24.1.3弧、弦、圆心角1
(Arc / chord / central angle)
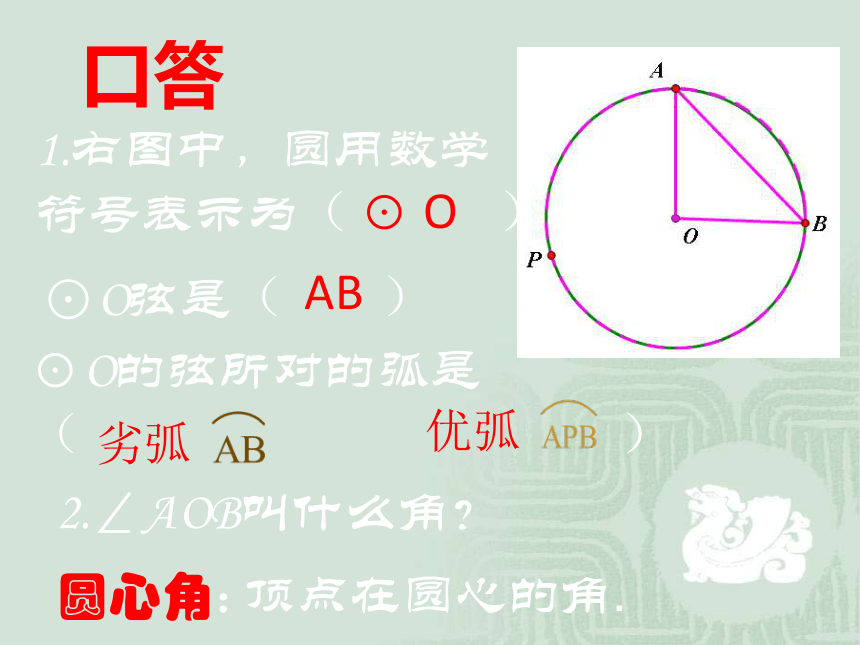
口答
1.右图中,圆用数学符号表示为( )
⊙ O
⊙O弦是( )
AB
⊙O的弦所对的弧是( )
优弧
劣弧
圆心角:
2.∠AOB叫什么角?
顶点在圆心的角.
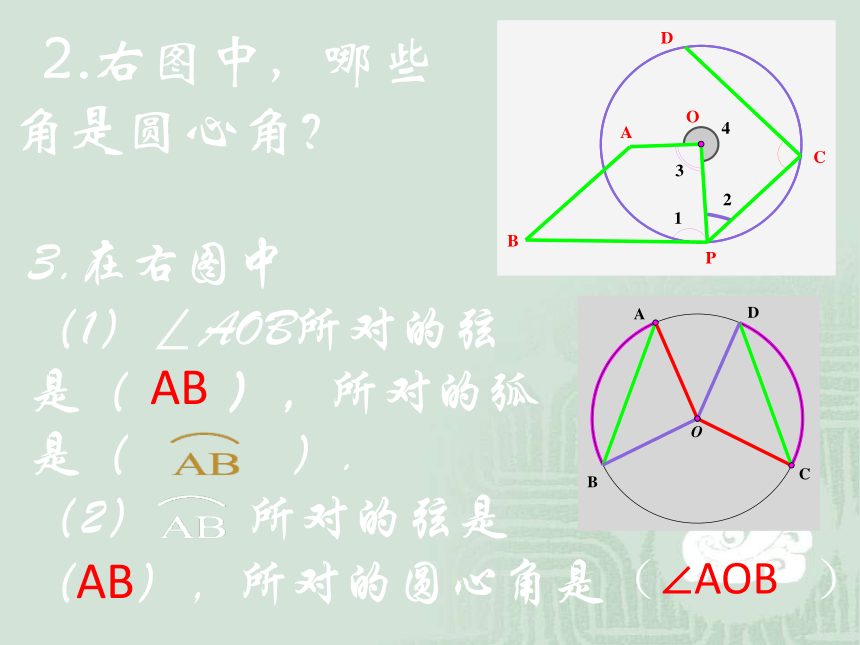
2.右图中,哪些角是圆心角?
3.在右图中
(1)∠AOB所对的弦
是( ),所对的弧
是( ).
(2) 所对的弦是
( ),所对的圆心角是( )
AB
AB
∠AOB
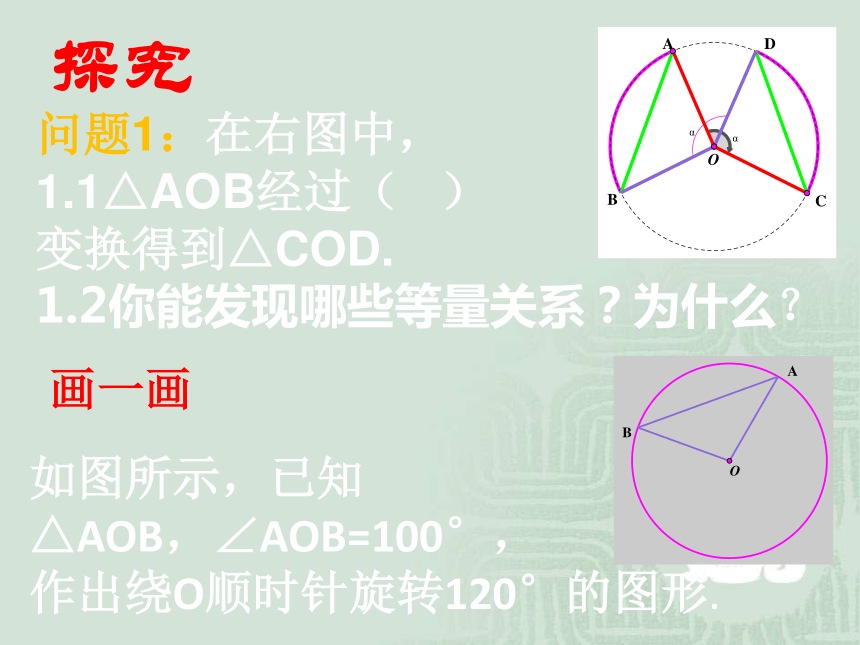
问题1:在右图中,
1.1△AOB经过( )
变换得到△COD.
1.2你能发现哪些等量关系?为什么?
探究
如图所示,已知
△AOB,∠AOB=100°,
作出绕O顺时针旋转120°的图形.
画一画
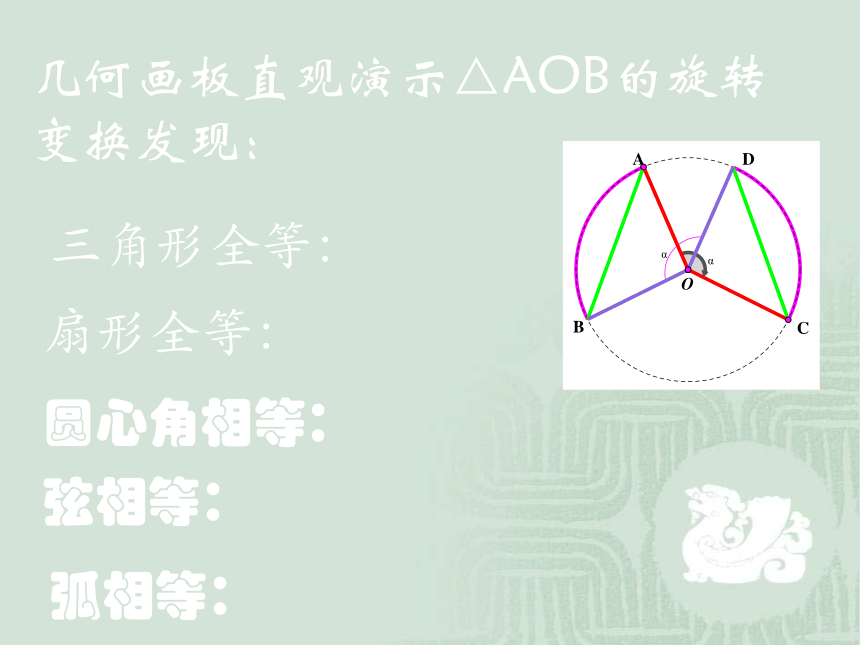
几何画板直观演示△AOB的旋转变换发现:
圆心角相等:
弦相等:
弧相等:
三角形全等:
扇形全等:
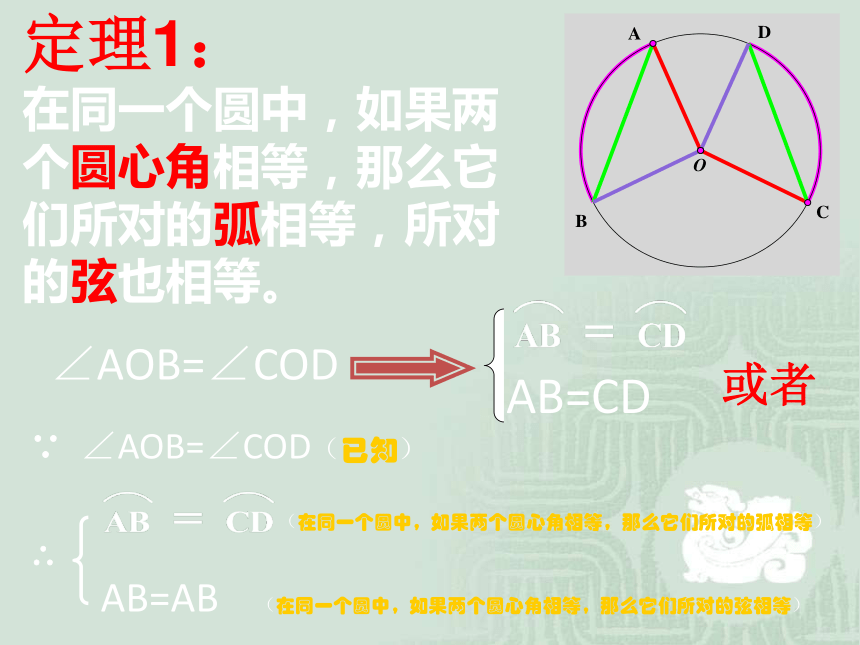
定理1:
在同一个圆中,如果两
个圆心角相等,那么它
们所对的弧相等,所对
的弦也相等。
∠AOB=∠COD
AB=CD
或者
∵ ∠AOB=∠COD(已知)
(在同一个圆中,如果两个圆心角相等,那么它们所对的弧相等) ∴
AB=AB (在同一个圆中,如果两个圆心角相等,那么它们所对的弦相等)
思考
如图∠1=∠2=∠3,
定理1结论还成立吗?
∠1=∠2=∠3
AB=CD=EF
定理1-A:
在同一个圆中,相等的圆心角所对的弧
相等,所对的弦也相等.
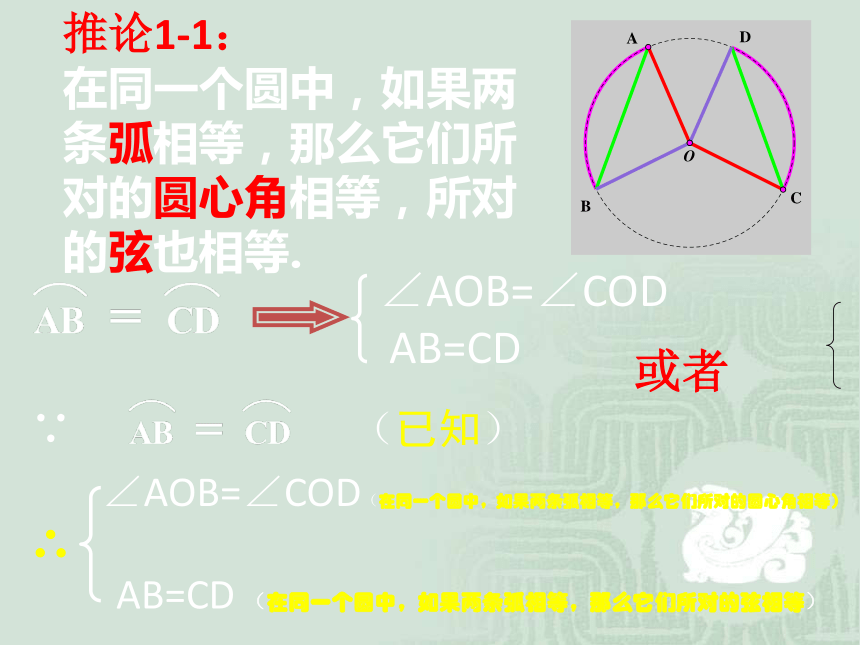
推论1-1:
在同一个圆中,如果两
条弧相等,那么它们所
对的圆心角相等,所对
的弦也相等.
∠AOB=∠COD
AB=CD
∵ (已知)
或者
∠AOB=∠COD(在同一个圆中,如果两条弧相等,那么它们所对的圆心角相等)
∴
AB=CD (在同一个圆中,如果两条弧相等,那么它们所对的弦相等)
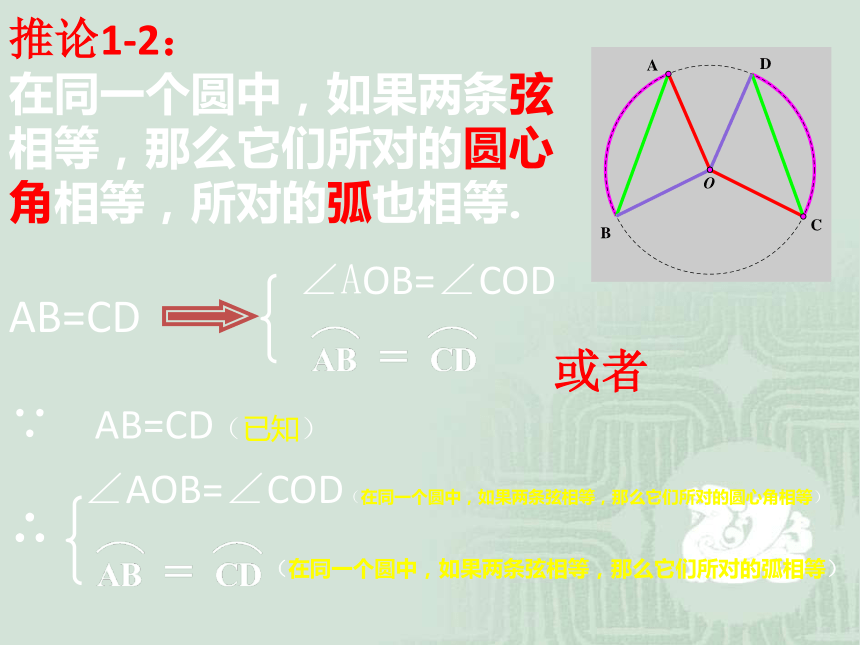
推论1-2:
在同一个圆中,如果两条弦
相等,那么它们所对的圆心
角相等,所对的弧也相等.
∵ AB=CD(已知)
AB=CD
∠AOB=∠COD
或者
∠AOB=∠COD(在同一个圆中,如果两条弦相等,那么它们所对的圆心角相等)
∴
(在同一个圆中,如果两条弦相等,那么它们所对的弧相等)
探究拓展
问题2:在两个等圆中,两个相等的圆心角所对的弧相等吗?所对的弦也相等吗?为什么?
想一想能否用前面探究问题1的思维方式来解决问题,怎样求解?
在右图中,
⊙O和⊙Y是
等圆,分别作相等的圆心角∠AOB与∠CYD,移动⊙O,使O 与Y重合,固定圆心,将⊙O旋转一个角度,使得OA与YC重合,你能发现那些等量关系?
试一试
现在,探究拓展的问题2就转化
成前面探究的问题1结论了,这
种解决问题的思维方式是一种重
要的数学思想方法
根据定理1、推论1-1、推论1-2可推得定理2、推论2-1、推论2-2
------化归思想.化未知为已知.
老师点拨
定理2
在等圆中,如
果两个圆心角
相等,那么它
们所对的两条弧相等,所对的弦也相等.
AB=CD
∠AOB=∠CYD
∴
(在同一个圆中,如果两条弦相等,那么它们所对的弧相等)
AB=CD(在同一个圆中,如果两个圆心角相等,那么它们所对的弦相等)
∵ ∠AOB= ∠ CYD(已知)
或者
推论2-1:
在等圆中,如
果两条弧相等,
那么它们所对
的圆心角相等,所对弦的也相等.
AB=CD
∠AOB=∠CYD
或者
∴
(在同一个圆中,如果两条弧相等,那么它们所对的弦相等)
∠AOB= ∠CYD(在同一个圆中,如果两条弧相等,那么它们所对的圆心角相等)
AB=CD
∵ (已知)
推论2-2:
在等圆中,如
果两条弦相等,
那么它们所对
的圆心角相等,所对的弧也相等.
AB=CD
∠AOB=∠CYD
∵ AB=CD(已知)
∴
(在同一个圆中,如果两条弦相等,那么它们所对的弧相等)
∠AOB=∠CYD(在同一个圆中,如果两条弦相等,那么它们所对的圆心角相等)
定理:
在同圆或等圆中,如果两个圆心角
相等,那么它们所对的弧相等,所
对的弦也相等.
教材P83(请同学们看书)
请同学们用3句话归纳上面的2个定理和4个推论:
合作交流
推论2:
在同圆或等圆中,如果两条弦相等,那么它们所对的所对的圆心角相等,所对的弧也相等.
推论1:
在同圆或等圆中,如果两条弧相等,那么它们所对的所对圆心角的相等,所对的弦也相等.
请同学们把教材P83的1个定理
和2个推论用1个定理描述:
在同圆或等圆中,两个圆心角、弧、弦
中有一组量相等,它们所对的其余各组量也相等.
弧、弦、圆心角的关系定理:
如图,在⊙O中,
∠ACB=60°,
求证∠AOB=∠AOC=∠BOC.
方法1:
例题讲解
分析法探索解题思路
综合法书写证明过程
方法2
分析:证△AOC和△BOC,再证∠ACO=∠BCO=30°,,∠AOC=∠BOC=120°
证明:
∵ (已知)
∴AB=AC(同圆中相等的弧所对的弦相等)
∴△ABC是等腰三角形(等腰三角形的定义)
∵∠ACB=60°(已知)
∴△ABC是等边三角形
(有一个角是60°的等腰三角形是等边三角形)
∴AB=AC=BC(等边三角形的定义)
∴∠AOB=∠AOC=∠BOC(同圆中相等的弦所对的圆心角相等)
1.圆心角的概念.
2.弧、弦、圆心角的关系定理:
在同圆或等圆中,两个圆心角、弧、弦
中有一组量相等,它们所对的其余各组
量也相等。
3.利用弧、弦、圆心角的关系定理解决
一些具体问题.
课堂小结
本节课应掌握
1.复习教材P82-83,
回忆讲课思路.
2.教材P87,复习巩固2,3,
教材P88,综合应用11.
3. 作业批改后反思改错,
把错题记录在错题本上.
24.1.3弧、弦、圆心角1
(Arc / chord / central angle)
口答
1.右图中,圆用数学符号表示为( )
⊙ O
⊙O弦是( )
AB
⊙O的弦所对的弧是( )
优弧
劣弧
圆心角:
2.∠AOB叫什么角?
顶点在圆心的角.
2.右图中,哪些角是圆心角?
3.在右图中
(1)∠AOB所对的弦
是( ),所对的弧
是( ).
(2) 所对的弦是
( ),所对的圆心角是( )
AB
AB
∠AOB
问题1:在右图中,
1.1△AOB经过( )
变换得到△COD.
1.2你能发现哪些等量关系?为什么?
探究
如图所示,已知
△AOB,∠AOB=100°,
作出绕O顺时针旋转120°的图形.
画一画
几何画板直观演示△AOB的旋转变换发现:
圆心角相等:
弦相等:
弧相等:
三角形全等:
扇形全等:
定理1:
在同一个圆中,如果两
个圆心角相等,那么它
们所对的弧相等,所对
的弦也相等。
∠AOB=∠COD
AB=CD
或者
∵ ∠AOB=∠COD(已知)
(在同一个圆中,如果两个圆心角相等,那么它们所对的弧相等) ∴
AB=AB (在同一个圆中,如果两个圆心角相等,那么它们所对的弦相等)
思考
如图∠1=∠2=∠3,
定理1结论还成立吗?
∠1=∠2=∠3
AB=CD=EF
定理1-A:
在同一个圆中,相等的圆心角所对的弧
相等,所对的弦也相等.
推论1-1:
在同一个圆中,如果两
条弧相等,那么它们所
对的圆心角相等,所对
的弦也相等.
∠AOB=∠COD
AB=CD
∵ (已知)
或者
∠AOB=∠COD(在同一个圆中,如果两条弧相等,那么它们所对的圆心角相等)
∴
AB=CD (在同一个圆中,如果两条弧相等,那么它们所对的弦相等)
推论1-2:
在同一个圆中,如果两条弦
相等,那么它们所对的圆心
角相等,所对的弧也相等.
∵ AB=CD(已知)
AB=CD
∠AOB=∠COD
或者
∠AOB=∠COD(在同一个圆中,如果两条弦相等,那么它们所对的圆心角相等)
∴
(在同一个圆中,如果两条弦相等,那么它们所对的弧相等)
探究拓展
问题2:在两个等圆中,两个相等的圆心角所对的弧相等吗?所对的弦也相等吗?为什么?
想一想能否用前面探究问题1的思维方式来解决问题,怎样求解?
在右图中,
⊙O和⊙Y是
等圆,分别作相等的圆心角∠AOB与∠CYD,移动⊙O,使O 与Y重合,固定圆心,将⊙O旋转一个角度,使得OA与YC重合,你能发现那些等量关系?
试一试
现在,探究拓展的问题2就转化
成前面探究的问题1结论了,这
种解决问题的思维方式是一种重
要的数学思想方法
根据定理1、推论1-1、推论1-2可推得定理2、推论2-1、推论2-2
------化归思想.化未知为已知.
老师点拨
定理2
在等圆中,如
果两个圆心角
相等,那么它
们所对的两条弧相等,所对的弦也相等.
AB=CD
∠AOB=∠CYD
∴
(在同一个圆中,如果两条弦相等,那么它们所对的弧相等)
AB=CD(在同一个圆中,如果两个圆心角相等,那么它们所对的弦相等)
∵ ∠AOB= ∠ CYD(已知)
或者
推论2-1:
在等圆中,如
果两条弧相等,
那么它们所对
的圆心角相等,所对弦的也相等.
AB=CD
∠AOB=∠CYD
或者
∴
(在同一个圆中,如果两条弧相等,那么它们所对的弦相等)
∠AOB= ∠CYD(在同一个圆中,如果两条弧相等,那么它们所对的圆心角相等)
AB=CD
∵ (已知)
推论2-2:
在等圆中,如
果两条弦相等,
那么它们所对
的圆心角相等,所对的弧也相等.
AB=CD
∠AOB=∠CYD
∵ AB=CD(已知)
∴
(在同一个圆中,如果两条弦相等,那么它们所对的弧相等)
∠AOB=∠CYD(在同一个圆中,如果两条弦相等,那么它们所对的圆心角相等)
定理:
在同圆或等圆中,如果两个圆心角
相等,那么它们所对的弧相等,所
对的弦也相等.
教材P83(请同学们看书)
请同学们用3句话归纳上面的2个定理和4个推论:
合作交流
推论2:
在同圆或等圆中,如果两条弦相等,那么它们所对的所对的圆心角相等,所对的弧也相等.
推论1:
在同圆或等圆中,如果两条弧相等,那么它们所对的所对圆心角的相等,所对的弦也相等.
请同学们把教材P83的1个定理
和2个推论用1个定理描述:
在同圆或等圆中,两个圆心角、弧、弦
中有一组量相等,它们所对的其余各组量也相等.
弧、弦、圆心角的关系定理:
如图,在⊙O中,
∠ACB=60°,
求证∠AOB=∠AOC=∠BOC.
方法1:
例题讲解
分析法探索解题思路
综合法书写证明过程
方法2
分析:证△AOC和△BOC,再证∠ACO=∠BCO=30°,,∠AOC=∠BOC=120°
证明:
∵ (已知)
∴AB=AC(同圆中相等的弧所对的弦相等)
∴△ABC是等腰三角形(等腰三角形的定义)
∵∠ACB=60°(已知)
∴△ABC是等边三角形
(有一个角是60°的等腰三角形是等边三角形)
∴AB=AC=BC(等边三角形的定义)
∴∠AOB=∠AOC=∠BOC(同圆中相等的弦所对的圆心角相等)
1.圆心角的概念.
2.弧、弦、圆心角的关系定理:
在同圆或等圆中,两个圆心角、弧、弦
中有一组量相等,它们所对的其余各组
量也相等。
3.利用弧、弦、圆心角的关系定理解决
一些具体问题.
课堂小结
本节课应掌握
1.复习教材P82-83,
回忆讲课思路.
2.教材P87,复习巩固2,3,
教材P88,综合应用11.
3. 作业批改后反思改错,
把错题记录在错题本上.
同课章节目录
