2020-2021学年青岛新版七年级上册数学《第1章 基本的几何图形》单元测试卷(Word版 含解析)
文档属性
| 名称 | 2020-2021学年青岛新版七年级上册数学《第1章 基本的几何图形》单元测试卷(Word版 含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 193.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-10 23:06:20 | ||
图片预览


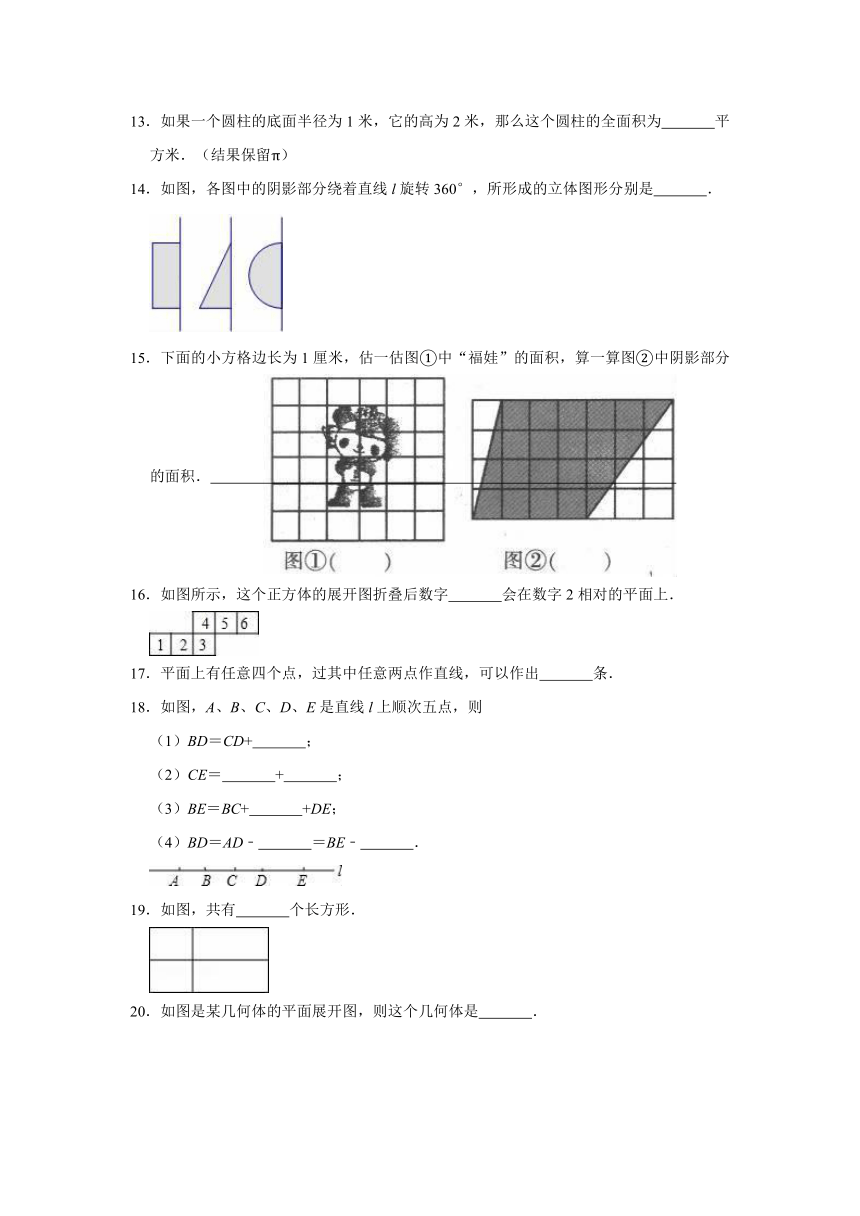


文档简介
2020-2021学年青岛新版七年级上册数学《第1章
基本的几何图形》单元测试卷
一.选择题
1.足球的表面是由什么图形缝制而成的( )
A.圆形
B.五边形和六边形
C.六边形
D.不规则图形
2.下图中甲和乙周长相比,结果是( )
A.甲比乙大
B.甲比乙小
C.甲和乙一样大
D.无法比较
3.给出以下四种说法:
(1)矩形绕着它的一条边旋转一周,形成圆柱;
(2)梯形绕着它的下底旋转一周,形成圆柱;
(3)直角三角形绕着它的一条直角边旋转一周,形成圆锥;
(4)直角梯形绕着垂直于底边的腰旋转一周,形成圆锥.
其中,说法正确的是( )
A.(1)(2)
B.(1)(3)
C.(2)(3)
D.(2)(4)
4.一个正方体的表面展开图可以是下列图形中的( )
A.
B.
C.
D.
5.下列图形中,经过折叠可围成长方体的是( )
A.
B.
C.
D.
6.小明掷骰子游戏,连续四次掷出的结果如图所示,请问第四次掷出的结果中底面上的数字是( )
A.2
B.5
C.3
D.以上都错
7.下列语句中,最正确的是( )
A.延长线段AB
B.延长射线AB
C.在直线AB的延长线上取一点C
D.延长线段BA到C,使BC=AB
8.如图,从A到B有3条路径,最短的路径是③,理由是( )
A.因为③是直的
B.两点确定一条直线
C.两点间距离的定义
D.两点之间,线段最短
9.反向延长线段AB到C使得BC=2AB,则下列关系式正确的为( )
A.AC=3AB
B.AC=2AB
C.AC=AB
D.AC=AB
10.如图,用一个平面去截一个正方体,截面相同的是( )
A.①与②
B.③与④
C.①与③④
D.①与②,③与④
二.填空题
11.用一个平面去截五棱柱,边数最多的截面是
形.
12.如图,AC=
+
,AB=
﹣
;若B为线段AC的中点,则AB=
=
,AC=2
=2
.
13.如果一个圆柱的底面半径为1米,它的高为2米,那么这个圆柱的全面积为
平方米.(结果保留π)
14.如图,各图中的阴影部分绕着直线l旋转360°,所形成的立体图形分别是
.
15.下面的小方格边长为1厘米,估一估图①中“福娃”的面积,算一算图②中阴影部分的面积.
16.如图所示,这个正方体的展开图折叠后数字
会在数字2相对的平面上.
17.平面上有任意四个点,过其中任意两点作直线,可以作出
条.
18.如图,A、B、C、D、E是直线l上顺次五点,则
(1)BD=CD+
;
(2)CE=
+
;
(3)BE=BC+
+DE;
(4)BD=AD﹣
=BE﹣
.
19.如图,共有
个长方形.
20.如图是某几何体的平面展开图,则这个几何体是
.
三.解答题
21.一间长为8米,宽为5米的房间,用半径为0.2米的圆形磨光机磨地板,不能磨到的部分的面积共多少平方米?(提示:不论房间面积多大,其四个角各有一部分不能磨到)
22.如图,立方体每个面上都写有一个自然数,并且相对两个面所写两数之和相等.若18的对面写的是质数a,14的对面写是质数b,35的对面写的是质数c,试求a2+b2+c2﹣ab﹣bc﹣ca的值.
23.木工检验木条的边线是否是直的,常常用眼睛从木条的一端向另一端望去,如果看到两个端点及这条边线中的各点都重合于一点,那么这条边线就是直的,你可以同伙伴试一试这个方法,并说一说其中的道理.
24.如图,已知线段a、b,画线段AB.
(1)画a+b
(2)画2a+b
(3)画2a﹣b.
25.如图所示是我们在运动场上踢的足球,而大多的足球是由许多小黑白块的皮缝合而成的.小强和小刚两位同学,一天在玩足球时研究起足球上的黑白块的个数,结果发现黑块都是五边形,白块都是六边形.小强好不容易才数清了黑块共12块,小刚数白块时不是重复,就是遗漏,无法数清白块的个数,你能帮助小刚解决这一问题吗?
26.如图,C,D,E将线段AB分成四部分,且AC:CD:DE:EB=2:3:4:5,M,P,Q,N分别是AC,CD,DE,BE的中点,若MN=a,求PQ的长.
参考答案与试题解析
一.选择题
1.解:足球表面是有一些正五边形和正六边形形构成的.
故选:B.
2.解:由题意知,两对边平行且相等,
甲周长为两邻边加中间一条线段,乙周长为相邻两边加中间一条边.
故甲乙周长相等.
故选:C.
3.解:(1)矩形绕着它的一条边旋转一周,形成圆柱,正确;
(2)梯形绕着它的下底旋转一周,不形成圆柱,错误;
(3)直角三角形绕着它的一条直角边旋转一周,形成圆锥,正确;
(4)直角梯形绕着垂直于底边的腰旋转一周,形成圆台,错误.
正确的是(1)(3).
故选:B.
4.解:A,B,D折叠后有重合面,从而缺少面,不能折成正方体,只有C是一个正方体的表面展开图.
故选:C.
5.解:选项A缺少一个面,不能围成长方体;
选项C与D中折叠后底面重合,不能围成长方体;
只有B能围成长方体.
故选:B.
6.解:由图可知,与5相邻的面有1、2、3、4,
所以,“5”与“6”是相对面,
与1相邻的面有2、4、5、6,
所以,“1”与“3”是相对面,
所以,“2”与“4”是相对面,
故第四次掷出的结果中底面上的数字是3.
故选:C.
7.解:A、延长线段AB,说法正确,故A选项正确;
B、延长射线AB,因没说明射线的端点,故B选项错误;
C、在直线AB的延长线上取一点C,因为直线不需延长,故C选项错误;
D、延长线段BA到C,使BC=AB,因为BC>AB,故D选项错误.
故选:A.
8.解:走路径③,是因为路径③是一条直线,而两点之间,线段最短.故选D.
9.解:由题意得,BC=BA+AC=2AB,
∴AC=AB.
故选:C.
10.解:由图形可知截面相同的是①与②,③与④.
故选:D.
二.填空题
11.解:用一个平面去截五棱柱,边数最多的截面是七边形.
故答案为:七边.
12.解:由图形可以看出,
AC=AB+BC,
AB=AC﹣BC,
∵B为线段AC的中点,
∴AB=BC=AC,AC=2AB=2BC,
故答案为:AB,BC,AC,BC,BC,AC,AB,BC.
13.解:根据圆柱的侧面积公式可得:π×2×1×2=4π.
圆柱的两个底面积为2π,
∴圆柱的全面积为4π+2π=6π(平方米).
故答案为:6π.
14.解:根据分析可得:各图中的阴影图形绕着直线l旋转360°,各能形成圆柱、圆锥、球.
故答案为:圆柱、圆锥、球.
15.解:小方格边长为1厘米,则一个小方格面积为1平方厘米.
(1)图中福娃约占了8个小方格,故答案为8平方厘米.
(2)图中阴影部分约占了20个小方格,故答案为20平方厘米.
16.解:面“1”与面“3”相对,面“2”与面“5”相对,“4”与面“6”相对.
故答案为:5.
17.解:如图所示,共可作1或4或6条直线.
故答案为:1或4或6.
18.解:A、B、C、D、E是直线上顺次五点,由图可知:
(1)BD=CD+BC,
(2)CE=CD+DE,
(3)BE=BC+CD+DE,
(4)BD=AD﹣AB=BE﹣DE.
故答案为:BC;CD,DE;CD;AB,DE.
19.解:如图,
长方形AHGE,EGJD,HBNG,GFCJ,HBCJ,AHJD,ABFE,EFCD,ABCD,
故答案为:9.
20.解:由几何体展开图可知,该几何体是三棱柱,
故答案为:三棱柱.
三.解答题
21.解:如图所示,
要求的面积=4(0.2×0.2﹣)=0.16﹣0.04π(平方米).
答:不能磨到的部分的面积共0.16﹣0.04π平方米.
22.解:∵35﹣18=17,
35﹣14=21,
∴35、18、14的对面数字都是质数,
∴35的对面是最小的质数2,
∴c=2,
∵相对两个面所写两数之和相等,
∴a=(35+2)﹣18=19,
b=(35+2)﹣14=23,
∴2(a2+b2+c2﹣ab﹣bc﹣ca)
=2(a2+b2+c2﹣ab﹣bc﹣ca)
=(a2﹣2ab+b2)+(a2﹣2ac+c2)+(b2﹣2bc+c2)
=(a﹣b)2+(a﹣c)2+(b﹣c)2
=(19﹣23)2+(19﹣2)2+(23﹣2)2
=16+289+441
=746.
∴a2+b2+c2﹣ab﹣bc﹣ca=×746=373.
23.解:如图,有3条线段,它们分别是线段AB,线段BC,线段AC,
∵两个端点及这条边线中的各点都重合于一点,根据经过两点有且只有一条直线,
∴这条线的边线是直的.
24.解:(1)如图所示,画线段AC使AC=a,再延长AC至B,使BC=b,则线段AB即为所求线段;
(2)如图所示,线段AC=2a,BC=b,则线段AB=2a+b;
(3)如图所示,AC=2a,BC=b,则AB=2a﹣b.
25.解:设白块有x块,则:3x=5×12,
解得:x=20.
答:白块有20块.
26.解:由AC:CD:DE:EB=2:3:4:5,得
AC=2x,CD=3x,DE=4x,EB=5x.
由M是AC的中点,N是BE的中点,得
AM=AC=x,NB=EB=.
由线段的和差,得
MN=MC+CD+DE+EN=x+3x+4x+x=.
又MN=a,
=a.
解得x=.
由P是CD的中点,Q是DE的中点,得
PD=CD=,DQ=DE=2x.
PQ=PD+DQ=+2x=
PQ=×=a.
基本的几何图形》单元测试卷
一.选择题
1.足球的表面是由什么图形缝制而成的( )
A.圆形
B.五边形和六边形
C.六边形
D.不规则图形
2.下图中甲和乙周长相比,结果是( )
A.甲比乙大
B.甲比乙小
C.甲和乙一样大
D.无法比较
3.给出以下四种说法:
(1)矩形绕着它的一条边旋转一周,形成圆柱;
(2)梯形绕着它的下底旋转一周,形成圆柱;
(3)直角三角形绕着它的一条直角边旋转一周,形成圆锥;
(4)直角梯形绕着垂直于底边的腰旋转一周,形成圆锥.
其中,说法正确的是( )
A.(1)(2)
B.(1)(3)
C.(2)(3)
D.(2)(4)
4.一个正方体的表面展开图可以是下列图形中的( )
A.
B.
C.
D.
5.下列图形中,经过折叠可围成长方体的是( )
A.
B.
C.
D.
6.小明掷骰子游戏,连续四次掷出的结果如图所示,请问第四次掷出的结果中底面上的数字是( )
A.2
B.5
C.3
D.以上都错
7.下列语句中,最正确的是( )
A.延长线段AB
B.延长射线AB
C.在直线AB的延长线上取一点C
D.延长线段BA到C,使BC=AB
8.如图,从A到B有3条路径,最短的路径是③,理由是( )
A.因为③是直的
B.两点确定一条直线
C.两点间距离的定义
D.两点之间,线段最短
9.反向延长线段AB到C使得BC=2AB,则下列关系式正确的为( )
A.AC=3AB
B.AC=2AB
C.AC=AB
D.AC=AB
10.如图,用一个平面去截一个正方体,截面相同的是( )
A.①与②
B.③与④
C.①与③④
D.①与②,③与④
二.填空题
11.用一个平面去截五棱柱,边数最多的截面是
形.
12.如图,AC=
+
,AB=
﹣
;若B为线段AC的中点,则AB=
=
,AC=2
=2
.
13.如果一个圆柱的底面半径为1米,它的高为2米,那么这个圆柱的全面积为
平方米.(结果保留π)
14.如图,各图中的阴影部分绕着直线l旋转360°,所形成的立体图形分别是
.
15.下面的小方格边长为1厘米,估一估图①中“福娃”的面积,算一算图②中阴影部分的面积.
16.如图所示,这个正方体的展开图折叠后数字
会在数字2相对的平面上.
17.平面上有任意四个点,过其中任意两点作直线,可以作出
条.
18.如图,A、B、C、D、E是直线l上顺次五点,则
(1)BD=CD+
;
(2)CE=
+
;
(3)BE=BC+
+DE;
(4)BD=AD﹣
=BE﹣
.
19.如图,共有
个长方形.
20.如图是某几何体的平面展开图,则这个几何体是
.
三.解答题
21.一间长为8米,宽为5米的房间,用半径为0.2米的圆形磨光机磨地板,不能磨到的部分的面积共多少平方米?(提示:不论房间面积多大,其四个角各有一部分不能磨到)
22.如图,立方体每个面上都写有一个自然数,并且相对两个面所写两数之和相等.若18的对面写的是质数a,14的对面写是质数b,35的对面写的是质数c,试求a2+b2+c2﹣ab﹣bc﹣ca的值.
23.木工检验木条的边线是否是直的,常常用眼睛从木条的一端向另一端望去,如果看到两个端点及这条边线中的各点都重合于一点,那么这条边线就是直的,你可以同伙伴试一试这个方法,并说一说其中的道理.
24.如图,已知线段a、b,画线段AB.
(1)画a+b
(2)画2a+b
(3)画2a﹣b.
25.如图所示是我们在运动场上踢的足球,而大多的足球是由许多小黑白块的皮缝合而成的.小强和小刚两位同学,一天在玩足球时研究起足球上的黑白块的个数,结果发现黑块都是五边形,白块都是六边形.小强好不容易才数清了黑块共12块,小刚数白块时不是重复,就是遗漏,无法数清白块的个数,你能帮助小刚解决这一问题吗?
26.如图,C,D,E将线段AB分成四部分,且AC:CD:DE:EB=2:3:4:5,M,P,Q,N分别是AC,CD,DE,BE的中点,若MN=a,求PQ的长.
参考答案与试题解析
一.选择题
1.解:足球表面是有一些正五边形和正六边形形构成的.
故选:B.
2.解:由题意知,两对边平行且相等,
甲周长为两邻边加中间一条线段,乙周长为相邻两边加中间一条边.
故甲乙周长相等.
故选:C.
3.解:(1)矩形绕着它的一条边旋转一周,形成圆柱,正确;
(2)梯形绕着它的下底旋转一周,不形成圆柱,错误;
(3)直角三角形绕着它的一条直角边旋转一周,形成圆锥,正确;
(4)直角梯形绕着垂直于底边的腰旋转一周,形成圆台,错误.
正确的是(1)(3).
故选:B.
4.解:A,B,D折叠后有重合面,从而缺少面,不能折成正方体,只有C是一个正方体的表面展开图.
故选:C.
5.解:选项A缺少一个面,不能围成长方体;
选项C与D中折叠后底面重合,不能围成长方体;
只有B能围成长方体.
故选:B.
6.解:由图可知,与5相邻的面有1、2、3、4,
所以,“5”与“6”是相对面,
与1相邻的面有2、4、5、6,
所以,“1”与“3”是相对面,
所以,“2”与“4”是相对面,
故第四次掷出的结果中底面上的数字是3.
故选:C.
7.解:A、延长线段AB,说法正确,故A选项正确;
B、延长射线AB,因没说明射线的端点,故B选项错误;
C、在直线AB的延长线上取一点C,因为直线不需延长,故C选项错误;
D、延长线段BA到C,使BC=AB,因为BC>AB,故D选项错误.
故选:A.
8.解:走路径③,是因为路径③是一条直线,而两点之间,线段最短.故选D.
9.解:由题意得,BC=BA+AC=2AB,
∴AC=AB.
故选:C.
10.解:由图形可知截面相同的是①与②,③与④.
故选:D.
二.填空题
11.解:用一个平面去截五棱柱,边数最多的截面是七边形.
故答案为:七边.
12.解:由图形可以看出,
AC=AB+BC,
AB=AC﹣BC,
∵B为线段AC的中点,
∴AB=BC=AC,AC=2AB=2BC,
故答案为:AB,BC,AC,BC,BC,AC,AB,BC.
13.解:根据圆柱的侧面积公式可得:π×2×1×2=4π.
圆柱的两个底面积为2π,
∴圆柱的全面积为4π+2π=6π(平方米).
故答案为:6π.
14.解:根据分析可得:各图中的阴影图形绕着直线l旋转360°,各能形成圆柱、圆锥、球.
故答案为:圆柱、圆锥、球.
15.解:小方格边长为1厘米,则一个小方格面积为1平方厘米.
(1)图中福娃约占了8个小方格,故答案为8平方厘米.
(2)图中阴影部分约占了20个小方格,故答案为20平方厘米.
16.解:面“1”与面“3”相对,面“2”与面“5”相对,“4”与面“6”相对.
故答案为:5.
17.解:如图所示,共可作1或4或6条直线.
故答案为:1或4或6.
18.解:A、B、C、D、E是直线上顺次五点,由图可知:
(1)BD=CD+BC,
(2)CE=CD+DE,
(3)BE=BC+CD+DE,
(4)BD=AD﹣AB=BE﹣DE.
故答案为:BC;CD,DE;CD;AB,DE.
19.解:如图,
长方形AHGE,EGJD,HBNG,GFCJ,HBCJ,AHJD,ABFE,EFCD,ABCD,
故答案为:9.
20.解:由几何体展开图可知,该几何体是三棱柱,
故答案为:三棱柱.
三.解答题
21.解:如图所示,
要求的面积=4(0.2×0.2﹣)=0.16﹣0.04π(平方米).
答:不能磨到的部分的面积共0.16﹣0.04π平方米.
22.解:∵35﹣18=17,
35﹣14=21,
∴35、18、14的对面数字都是质数,
∴35的对面是最小的质数2,
∴c=2,
∵相对两个面所写两数之和相等,
∴a=(35+2)﹣18=19,
b=(35+2)﹣14=23,
∴2(a2+b2+c2﹣ab﹣bc﹣ca)
=2(a2+b2+c2﹣ab﹣bc﹣ca)
=(a2﹣2ab+b2)+(a2﹣2ac+c2)+(b2﹣2bc+c2)
=(a﹣b)2+(a﹣c)2+(b﹣c)2
=(19﹣23)2+(19﹣2)2+(23﹣2)2
=16+289+441
=746.
∴a2+b2+c2﹣ab﹣bc﹣ca=×746=373.
23.解:如图,有3条线段,它们分别是线段AB,线段BC,线段AC,
∵两个端点及这条边线中的各点都重合于一点,根据经过两点有且只有一条直线,
∴这条线的边线是直的.
24.解:(1)如图所示,画线段AC使AC=a,再延长AC至B,使BC=b,则线段AB即为所求线段;
(2)如图所示,线段AC=2a,BC=b,则线段AB=2a+b;
(3)如图所示,AC=2a,BC=b,则AB=2a﹣b.
25.解:设白块有x块,则:3x=5×12,
解得:x=20.
答:白块有20块.
26.解:由AC:CD:DE:EB=2:3:4:5,得
AC=2x,CD=3x,DE=4x,EB=5x.
由M是AC的中点,N是BE的中点,得
AM=AC=x,NB=EB=.
由线段的和差,得
MN=MC+CD+DE+EN=x+3x+4x+x=.
又MN=a,
=a.
解得x=.
由P是CD的中点,Q是DE的中点,得
PD=CD=,DQ=DE=2x.
PQ=PD+DQ=+2x=
PQ=×=a.
同课章节目录
- 第1章 基本的几何图形
- 1.1 我们身边的图形世界
- 1.2 几何图形
- 1.3 线段、射线和直线
- 1.4 线段的比较与作法
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数与绝对值
- 第3章 有理数的运算
- 3.1 有理数的加法与减法
- 3.2 有理数的乘法与除法
- 3.3 有理数的乘方
- 3.4 有理数的混合运算
- 3.5 利用计算器进行有理数的计算
- 第4章 数据的收集整理与描述
- 4.1 普查和抽样调查
- 4.2 简单随机抽样
- 4.3 数据的整理
- 4.4 扇形统计图
- 第5章 代数式与函数的初步认识
- 5.1 用字母表示数
- 5.2 代数式
- 5.3 代数式的值
- 5.4 生活中的常量与变量
- 5.5 函数的初步认识
- 第6章 整式的加减
- 6.1 单项式与多项式
- 6.2 同类项
- 6.3 去括号
- 6.4 整式的加减
- 第7章 一元一次方程
- 7.1 等式的基本性质
- 7.2 一元一次方程
- 7.3 一元一次方程的解法
- 7.4 一元一次方程的应用
