23.3 图案设计

(共32张PPT)
23.3 图案设计
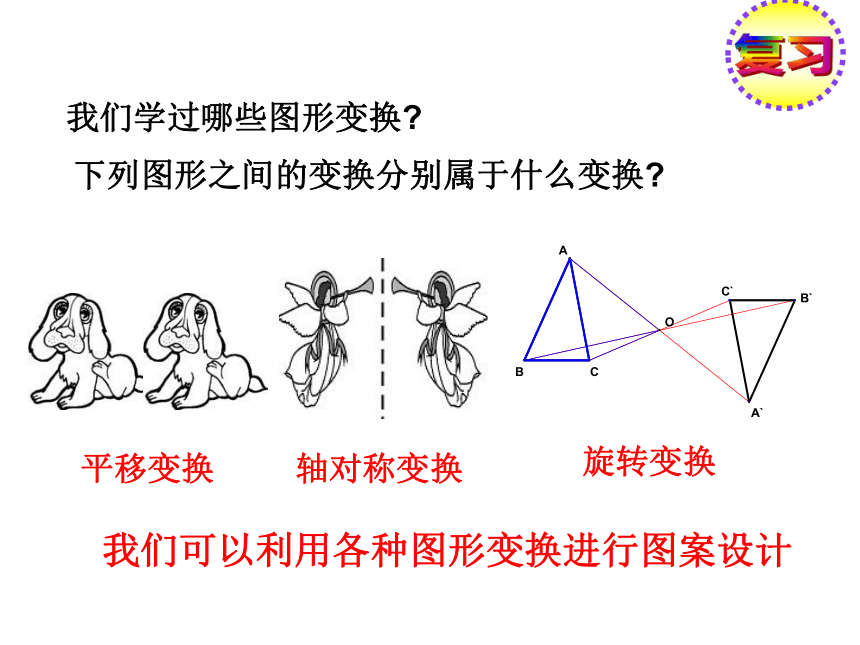
我们学过哪些图形变换
平移变换
轴对称变换
旋转变换
下列图形之间的变换分别属于什么变换
我们可以利用各种图形变换进行图案设计
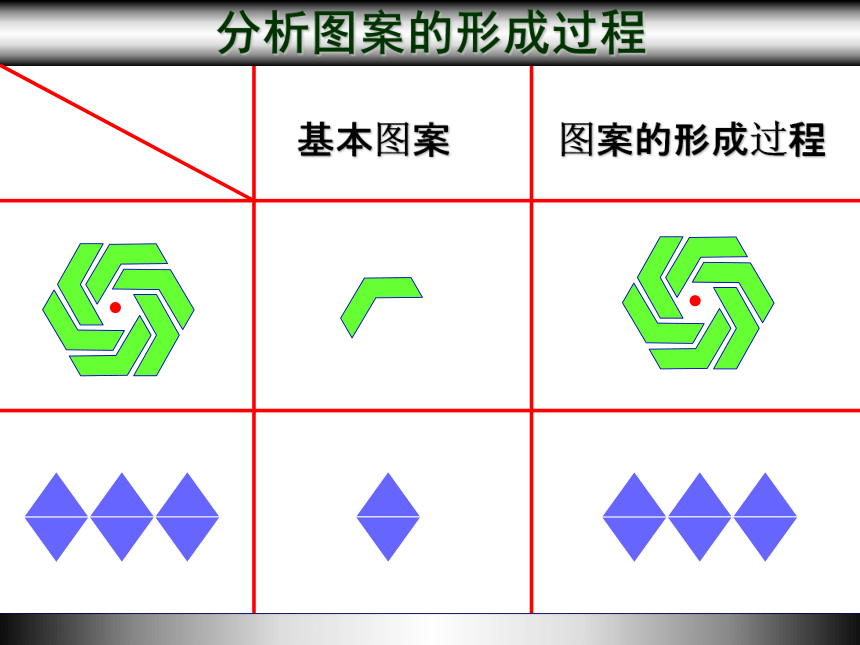
基本图案
图案的形成过程
分析图案的形成过程
基本图案
图案的形成过程
分析图案的形成过程
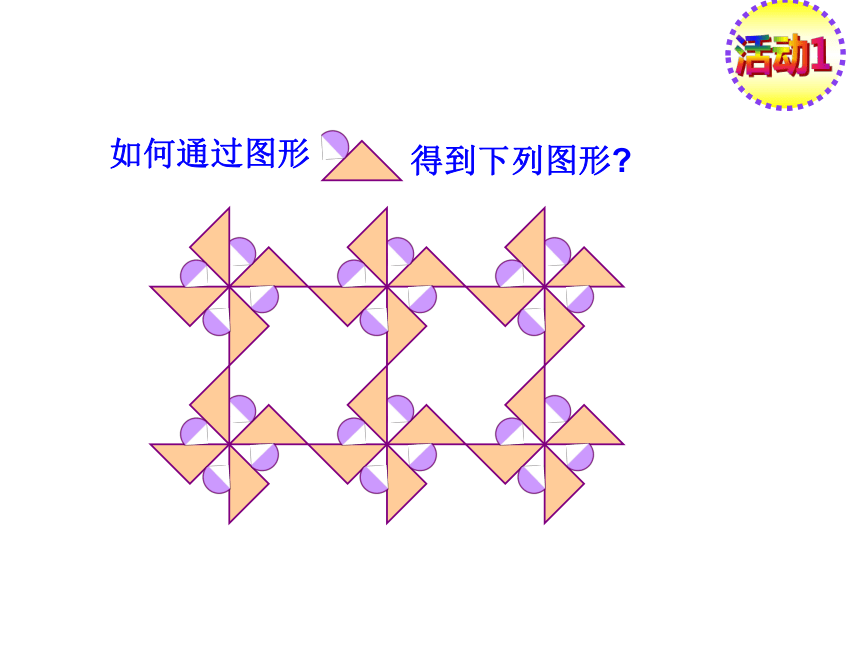
如何通过图形
得到下列图形
1.旋转:
将
逆时针旋转900、1800、2700
2.轴对称变换:
3.平移变换:
利用各种图形变换进行图案设计
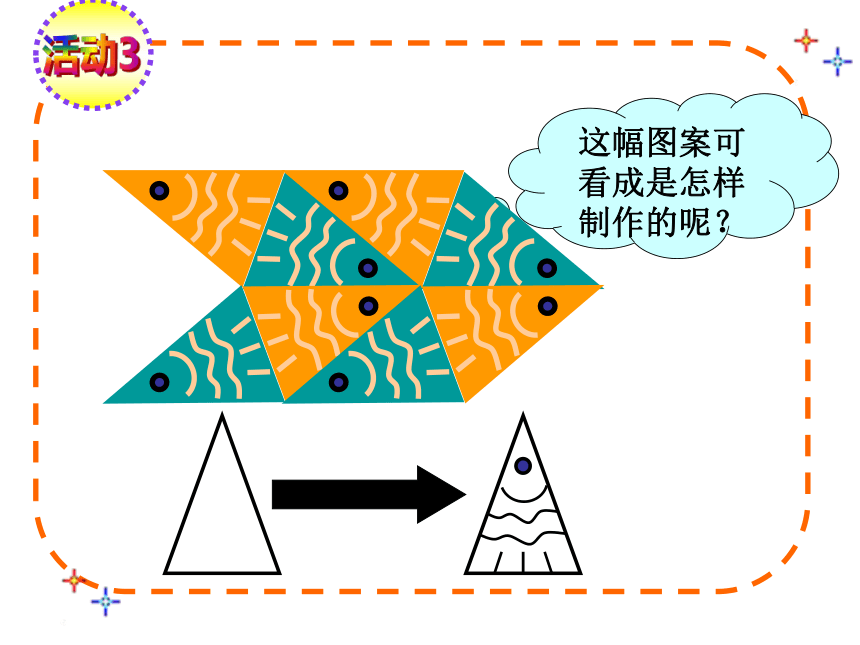
等积变形
3
4
1
2
1
2
2
1
3
4
中点
新旧图形的面积有何关系
面积相等
这幅图案可看成是怎样制作的呢？
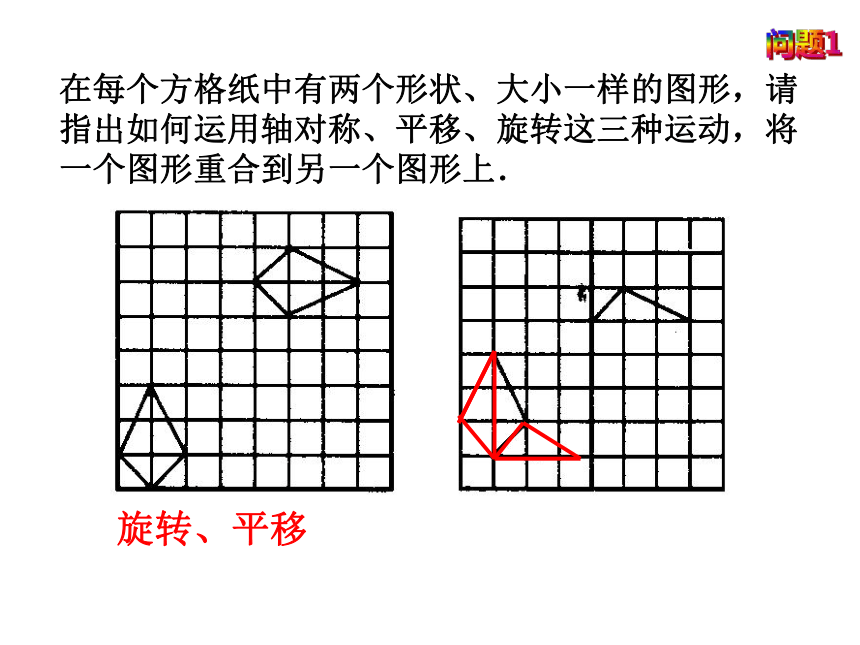
在每个方格纸中有两个形状、大小一样的图形，请指出如何运用轴对称、平移、旋转这三种运动，将一个图形重合到另一个图形上．
旋转、平移
已知，图A、图B分别是正方形网格上的两个中心对称图形，网格中最小的正方形面积为一个平方单位，则图A的面积为 ，图B的面积为 ；你能在图C的网格上画出一个面积为8个平方单位的中心对称图形吗？
12
12
A B C D
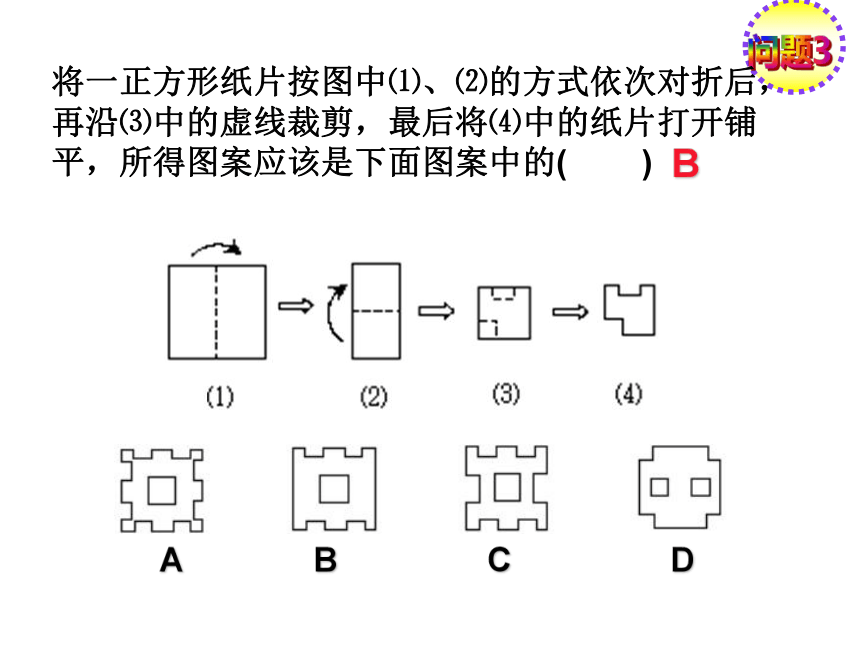
B
将一正方形纸片按图中⑴、⑵的方式依次对折后，再沿⑶中的虚线裁剪，最后将⑷中的纸片打开铺平，所得图案应该是下面图案中的( )
如图所示，把一个正方形三次对折后沿虚线剪下，所得图形是 ( )
C
(1)观察图中的①～④中的阴影部分构成的图案，请写出这四个图案都具有的两个共同特征；
(2)借助图⑤中的网格，请设计一个新的图案，使该图
同时具有你在解答(1)中所定的两个共同特征。
如图是五个小正方形拼成的图形.请你移动其中一个小正方形,重新拼成一个图形,使得所拼成的新图形:
(1)是轴对称图形,但不是中心对称图形;
(2)是中心对称图形,但不是轴对称图形;
(3)既是轴对称图形,又是中心对称图形.
(1)是轴对称图形,但不是中心对称图形;
(2)是中心对称图形,但不是轴对称图形;
(3)既是轴对称图形,又是中心对称图形.
请以给定的图形○○△△＝(两个圆,两个三角形,两条平行线)为构件,尽可能多地构思有意义的一些中心图形,并写上一两句贴切,诙谐的解说词.如下图就是符合要求的图形,你能构思其它图形吗 比一比,看谁想得多,看谁想得妙!
路灯与倒影
指南针
除号
沙漏
两只拔河的小鸡
小鸡
小鸟飞翔
鱼翔浅底
小猪小猪胖乎乎
唐老鸭溜冰
猫头鹰
蝴蝶纷飞
三毛他哥二毛
母女俩
开心雪人
用望远镜的小女孩
渔翁
请遵守交通规则
企盼奥运
流星雨
浪漫一刻
放飞心情
小雨伞
旭日东升
红旗飘扬
装甲车
飞碟
钥匙
宝剑
自行车
温暖的家
衬衣
把手
保护视力
天平
传送带
电灯
棒棒糖
红缨枪
直升飞机
圣诞树
手拉车
老上海电车
红绿灯
如何画平行线
下图是某设计师设计的方桌布图案的一部分。请你运用旋转变换的方法，在坐标纸上将该图形绕原点顺时针依次旋转90°，180°，270°，并画出它在各象限内的图形。
如图，O是边长为a的正方形ABCD的中心，将一块半径足够长，圆心角为直角的扇形纸板的圆心放在O点处，并将纸板绕O点旋转。则ABCD的边被纸板覆盖部分的面积为多少.
如图甲，正方形ABCD和正方形CEFG共一顶点C，且B，C，E在一条直线上。连接BG，DE.
请你猜测BG，DE的位置关系和数量关系，并说明理由；
若正方形CEFG绕C点顺时针方向旋转一个角度后，如图乙，BG和DE是否还有上述关系？是说明理由。
请选一个基本图形,从它出发进行图案设计.
在平面直角坐标系中，已知点P0的坐标为（1，0），将点P0绕着原点O按逆时针方向旋转30°得到点P1，延长OP1到点P2使O P2=2OP1；再将点P2绕原点O按逆时针方向旋转30°得到点P3，延长OP3到点P4使O P4=2OP3；……如此继续下去。求：
点P2的坐标；
点P2003的坐标.