13.3.1 实数(1)
图片预览








文档简介
(共29张PPT)
13.3.1 实数(1)
祖冲之(南北朝)
毕达哥拉斯
古希腊数学家
毕达哥拉斯学派
的主要代表人物
至2002年底,科学家们用超级计算机已把 值算到小数点后12411亿位.
边长为1的正方形对角线长到底是多少呢?这是怎样的一类数呢?
毕达哥拉斯学派认为“宇宙间的一切现象都能归结为整数或整数之比”,即都可用有理数来描述。但后来,这学派的一位成员希伯索斯发现边长为1的正方形的对角线的长不能用有理数来表示,这就动摇了毕达哥拉斯学派的信条,引起了信徒们的恐慌。由此引发了第一次数学危机。这是怎样的一类数呢?
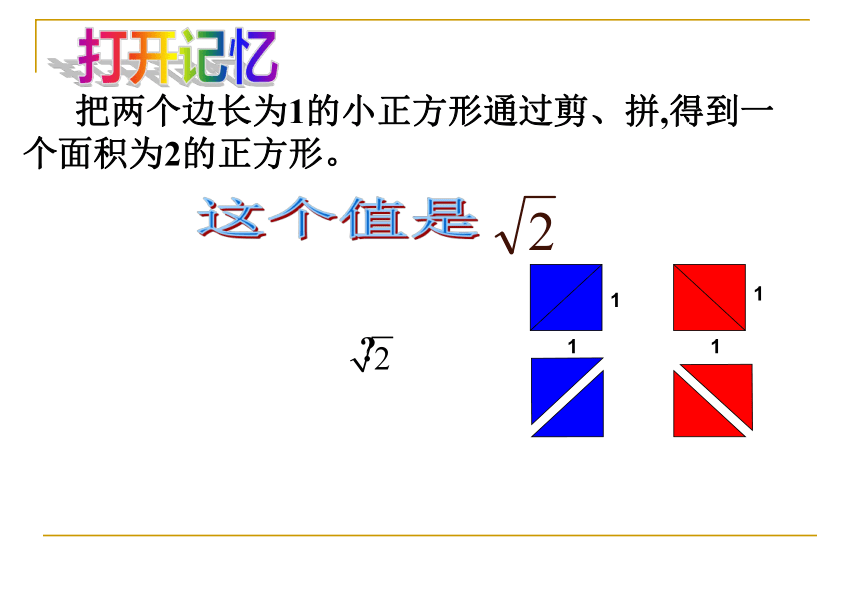
把两个边长为1的小正方形通过剪、拼,得到一个面积为2的正方形。
1
1
1
1
如果用计算机计算 ,结果将是:1.4142135623730950488016887242096980785696718753769480731766797379907324784621070388503875343276415727350138462309122970249248360558507372126441214970999358314132226659275055927557999505011527820605715……
有理数
整数
分数
使用计算器计算,把上述有理数写成小数的形式.
探究
3.0
- 0.6
5.875
你有什么发现?
★ 任何一个有理数都可以写成有限小数或无限循环小数的形式.
有限小数或
无限循环小数
如果用计算机计算 ,结果将是:1.4142135623730950488016887242096980785696718753769480731766797379907324784621070388503875343276415727350138462309122970249248360558507372126441214970999358314132226659275055927557999505011527820605715……
叫做无理数.
新知
… ①开不尽方的数
π … ②与π有关的数
1.010010001…
(两个1之间依次多一个0)
无限不循环小数
无理数的概念
你所认识的数中有没有不属于有理数的呢?说说看!
③无限有规律的数
无限不循环小数
无理数也像有理数一样广泛存在着。
实数的分类
实数
有理数
无理数
整数
分数
有限小数或无限循环小数
无限不循环小数
有理数和无理数统称实数.
有理数有正和负之分,那么无理数呢
无理数也有正负之分,例如
正无理数:
负无理数:
由于非0有理数和无理数都有正负之分.因此实数可有下面的分法.
⑧
①
②
③
④
⑤
⑥
⑦
依据实数的分类,在右图的卡片上填上下列数的名称.
正有理数
零
负有理数
正无理数
负无理数
有理数
无理数
实数
依据实数的分类,在右图的卡片上填上下列数的名称.
①
②
实数
③
④
⑤
⑥
⑦
⑧
正实数
零
负实数
正有理数
正无理数
负有理数
负无理数
几百年前的某一天,数字王国的国王准备挑选一位聪明的大臣出使塞外,于是召集他的大臣们开会。许多数字大臣纷纷到场,一时间会场里你推我挤,熙熙嚷嚷,吵个不休,国王非常生气。他该如何让大臣们有秩序的分类坐定下来呢?
数字王国
有理数集合
无理数集合
正实数集合
零
负实数集合
一、判断下列说法是否正确
3)实数可以分为正实数和负实数两类
……( )
1)无限小数都是无理数;
2)无理数都是无限小数;
………………………( )
………………………( )
4)实数不是有理数就是无理数 ……… ( )
5)带根号的数都是无理数 ……… ( )
6)无理数一定都带根号 ……… ( )
国王出题:
整数有
有理数有
无理数有
正实数有
实数有
二、填空
在实数
中,
,
,
,
p
0
0
p
p
0
,
,
0
p
国王出题:
大会召开圆满结束要退场了,国王为了防止出现
刚才你推我挤的场面,要求他们在数轴上先排好队。
这时无理数大臣们又嚷开了,我们能有自己准确的位
置吗?
如图,直径为1个单位长度的圆的周长为多少?把这个圆从原点沿数轴向 滚动一周,圆上一点从原点到达A点,则点A的坐标为多少?
-4
-2
0
1
2
3
4
-1
-3
无理数 可以用数轴上的点来表示.
A
问题2.你能在数轴上表示出 吗?
问题1.无理数能在数轴上表示出来吗?
左
右
探究
-2
-1
0
1
2
-
每一个实数都可以用数轴上的一个点来表示;
反过来,数轴上的每一个点都表示一个实数。
★实数与数轴上的点是一一对应的.
A
实数 a
探究
-2
-1
0
1
2
-
1
-2
-1
0
1
2
-1
1
x
y
A点的坐标是________
A
( , 0 )
B
B点的坐标是________
(0 , )
有序实数对
有序实数对和直角坐标系中的点是一一对应的.
当数从有理数扩充到实数以后,有理数关于相反数和绝对值等的意义同样适合于实数.
实数 的相反数是
一个正实数的绝对值是 ,一个负实数的
绝对值是 ,0的绝对值是 。
它本身
它的相反数
0
(1)请将数轴上是各点与下列实数对应起来:
-3 -2 -1 0 1 2 3 4
A
B
C
D
E
3
(2)比较它们的大小(用“<”号连接)
<
<
<
<
-1.5
3
在数轴上表示的两个实数,右边的数总比左边的数大。
π-3.14的相反数是_________
3.14-π
4
的相反数是
例:
(1) 的相反数是__________
(5) 绝对值是 _________
(2) 的倒数是____,
(3)| |=___________
(4)绝对值等于 的数是 _________
的平方 是___ .
(6)绝对值小于 的整数是___________
(7) 0
>
1、无理数和实数的概念;
2、实数的分类;
3、实数和数轴上的点是一一对应的;有序实数对和平面直角坐标系一一对应。
4、相反数、绝对值、数的大小比较法则同样适用于实数;
小结
思想方法:分类思想,类比思想,数形结合思想,化归思想
布置作业
1.作业本;
2.阅读课本88页“阅读与思考”为什么说 不是
有理数?
3.课外探究
你能在数轴上表示出 吗?
13.3.1 实数(1)
祖冲之(南北朝)
毕达哥拉斯
古希腊数学家
毕达哥拉斯学派
的主要代表人物
至2002年底,科学家们用超级计算机已把 值算到小数点后12411亿位.
边长为1的正方形对角线长到底是多少呢?这是怎样的一类数呢?
毕达哥拉斯学派认为“宇宙间的一切现象都能归结为整数或整数之比”,即都可用有理数来描述。但后来,这学派的一位成员希伯索斯发现边长为1的正方形的对角线的长不能用有理数来表示,这就动摇了毕达哥拉斯学派的信条,引起了信徒们的恐慌。由此引发了第一次数学危机。这是怎样的一类数呢?
把两个边长为1的小正方形通过剪、拼,得到一个面积为2的正方形。
1
1
1
1
如果用计算机计算 ,结果将是:1.4142135623730950488016887242096980785696718753769480731766797379907324784621070388503875343276415727350138462309122970249248360558507372126441214970999358314132226659275055927557999505011527820605715……
有理数
整数
分数
使用计算器计算,把上述有理数写成小数的形式.
探究
3.0
- 0.6
5.875
你有什么发现?
★ 任何一个有理数都可以写成有限小数或无限循环小数的形式.
有限小数或
无限循环小数
如果用计算机计算 ,结果将是:1.4142135623730950488016887242096980785696718753769480731766797379907324784621070388503875343276415727350138462309122970249248360558507372126441214970999358314132226659275055927557999505011527820605715……
叫做无理数.
新知
… ①开不尽方的数
π … ②与π有关的数
1.010010001…
(两个1之间依次多一个0)
无限不循环小数
无理数的概念
你所认识的数中有没有不属于有理数的呢?说说看!
③无限有规律的数
无限不循环小数
无理数也像有理数一样广泛存在着。
实数的分类
实数
有理数
无理数
整数
分数
有限小数或无限循环小数
无限不循环小数
有理数和无理数统称实数.
有理数有正和负之分,那么无理数呢
无理数也有正负之分,例如
正无理数:
负无理数:
由于非0有理数和无理数都有正负之分.因此实数可有下面的分法.
⑧
①
②
③
④
⑤
⑥
⑦
依据实数的分类,在右图的卡片上填上下列数的名称.
正有理数
零
负有理数
正无理数
负无理数
有理数
无理数
实数
依据实数的分类,在右图的卡片上填上下列数的名称.
①
②
实数
③
④
⑤
⑥
⑦
⑧
正实数
零
负实数
正有理数
正无理数
负有理数
负无理数
几百年前的某一天,数字王国的国王准备挑选一位聪明的大臣出使塞外,于是召集他的大臣们开会。许多数字大臣纷纷到场,一时间会场里你推我挤,熙熙嚷嚷,吵个不休,国王非常生气。他该如何让大臣们有秩序的分类坐定下来呢?
数字王国
有理数集合
无理数集合
正实数集合
零
负实数集合
一、判断下列说法是否正确
3)实数可以分为正实数和负实数两类
……( )
1)无限小数都是无理数;
2)无理数都是无限小数;
………………………( )
………………………( )
4)实数不是有理数就是无理数 ……… ( )
5)带根号的数都是无理数 ……… ( )
6)无理数一定都带根号 ……… ( )
国王出题:
整数有
有理数有
无理数有
正实数有
实数有
二、填空
在实数
中,
,
,
,
p
0
0
p
p
0
,
,
0
p
国王出题:
大会召开圆满结束要退场了,国王为了防止出现
刚才你推我挤的场面,要求他们在数轴上先排好队。
这时无理数大臣们又嚷开了,我们能有自己准确的位
置吗?
如图,直径为1个单位长度的圆的周长为多少?把这个圆从原点沿数轴向 滚动一周,圆上一点从原点到达A点,则点A的坐标为多少?
-4
-2
0
1
2
3
4
-1
-3
无理数 可以用数轴上的点来表示.
A
问题2.你能在数轴上表示出 吗?
问题1.无理数能在数轴上表示出来吗?
左
右
探究
-2
-1
0
1
2
-
每一个实数都可以用数轴上的一个点来表示;
反过来,数轴上的每一个点都表示一个实数。
★实数与数轴上的点是一一对应的.
A
实数 a
探究
-2
-1
0
1
2
-
1
-2
-1
0
1
2
-1
1
x
y
A点的坐标是________
A
( , 0 )
B
B点的坐标是________
(0 , )
有序实数对
有序实数对和直角坐标系中的点是一一对应的.
当数从有理数扩充到实数以后,有理数关于相反数和绝对值等的意义同样适合于实数.
实数 的相反数是
一个正实数的绝对值是 ,一个负实数的
绝对值是 ,0的绝对值是 。
它本身
它的相反数
0
(1)请将数轴上是各点与下列实数对应起来:
-3 -2 -1 0 1 2 3 4
A
B
C
D
E
3
(2)比较它们的大小(用“<”号连接)
<
<
<
<
-1.5
3
在数轴上表示的两个实数,右边的数总比左边的数大。
π-3.14的相反数是_________
3.14-π
4
的相反数是
例:
(1) 的相反数是__________
(5) 绝对值是 _________
(2) 的倒数是____,
(3)| |=___________
(4)绝对值等于 的数是 _________
的平方 是___ .
(6)绝对值小于 的整数是___________
(7) 0
>
1、无理数和实数的概念;
2、实数的分类;
3、实数和数轴上的点是一一对应的;有序实数对和平面直角坐标系一一对应。
4、相反数、绝对值、数的大小比较法则同样适用于实数;
小结
思想方法:分类思想,类比思想,数形结合思想,化归思想
布置作业
1.作业本;
2.阅读课本88页“阅读与思考”为什么说 不是
有理数?
3.课外探究
你能在数轴上表示出 吗?
