实数 (第一课时)
图片预览







文档简介
(共30张PPT)
口答: 9的平方根是____________
9的算术平方根是________
2的平方根是____________
2的算术平方根是________
3
复习提问
±3
问题1: 3、-3都是有理数吗
问题2: 都是有理数吗
10.3 实数 (第一课时)
知识回顾
1、有理数的概念
整数和分数统称为有理数.
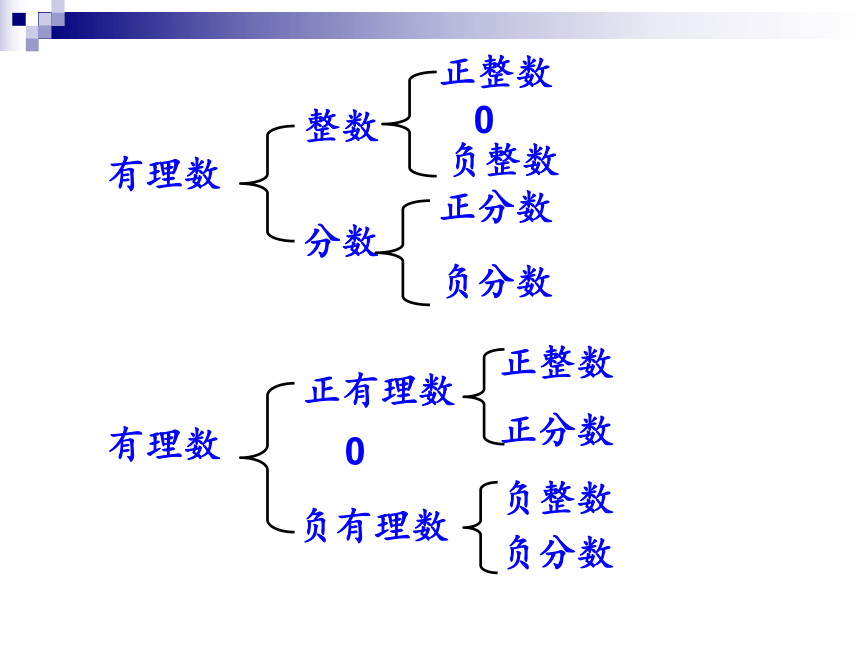
2、有理数的分类
有理数
分数
整数
正整数
0
负整数
正分数
负分数
有理数
正有理数
负有理数
0
正分数
正整数
负整数
负分数
探究一
借助计算器,把下列有理数写成小数的形式,你有什么发现?
5.875
3.0
- 0.6
·
2
1
0
.
任何一个有理数都可以写成有限小数或无限循环小数的形式.
反过来,任何有限小数或无限循环小数也都是有理数.
再使用计算器,把 写成小数的形式,你有什么发现?
我们把这种无限且不循环的小数叫做无理数.
1.41421356237309504880168…
公元前500年,古希腊毕达哥拉斯(Pythagoras)学派认为“万物皆为数”,即宇宙间的一切现象都能归结为整数与整数之比,也就是指一切现象都可用有理数来描述。
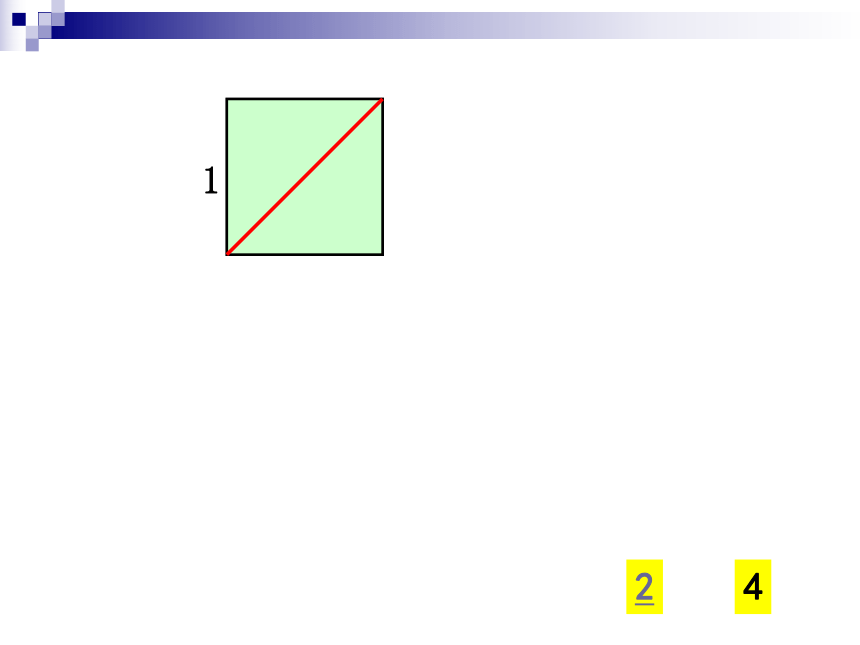
但后来这学派的成员希伯索斯(Hippasus) 发现边长为1的正方形的对角线的长不能用整数或整数之比来表示,这就动摇了毕达哥拉斯学派的信条,引起了信徒们的恐慌,据说,他为此被投入大海,为发现真理而献出宝贵的生命,但真理是不可战胜的。
你知道边长为1的正方形的对角线的长为多少吗?
1
4
2
1
A
D
C
B
E
F
M
N
1
1
2
2
除了 ,你能举出其他的一些无理数吗?
讨论:带根号的数都是无理数吗
说一说
有限小数或无限循环小数
无限不循环小数
有理数
无理数
练习:把下列各数分别填入相应的集合内
有理数集合
无理数集合
(相邻两个3之间
的7的个数逐次增加1个)
无理数也像有理数一样有正负之分.
无理数
正无理数
负无理数
(相邻两个3之间的7的个数逐次增加1个)
有理数和无理数统称为实数.
有理数
无理数
实数
初中阶段对数的认识范围扩充为
新加入
讨论交流:实数如何分类?
实数
有理数
正有理数
负有理数
零
无理数
正无理数
负无理数
或 有理数
整数
分数
实数
正实数
0
负实数
正有理数
正无理数
负有理数
负无理数
随堂练习
判断:
⑴实数不是有理数就是无理数。( )
⑵无理数都是无限不循环小数。( )
⑶无理数都是无限小数。( )
⑷带根号的数都是无理数。( )
⑸无理数一定都带根号。( )
⑹两个无理数之积不一定是无理数。( )
⑺两个无理数之和一定是无理数。( )
⑻数轴上的任何一点都可以表示实数。( )
×
×
×
如下图,以单位长度为边长画一个正方形,以原点为圆心,正方形对角线为半径画弧,与正、负半轴的交点分别为点A和点B,数轴上A点和B点对应的数是什么?
-2
-1
0
1
2
B
A
C
探究:每个有理数都可以用数轴上的点来表示.
无理数是否也可以用数轴上的点来表示出来呢
问题一:
无理数 可以用数轴上的点来表示出来.
OA的长是这个圆的周长 ,所以点A的坐标是
探究:每个有理数都可以用数轴上的点来表示.
无理数是否也可以用数轴上的点来表示出来呢
无理数 可以用数轴上的点来表示出来.
问题二:如图,直径为1个单位长度的圆从原点沿数轴向右滚动一周,圆上一点从原点到达A点,则点A的坐标为多少?
-4
-2
0
1
2
3
4
-1
-3
A
除了 ,其实所有的无理数都可以在数轴上表示出来,所以实数都可以在数轴上表示出来.
探究:每个有理数都可以用数轴上的点来表示.
无理数是否也可以用数轴上的点来表示出来呢
0
1
2
3
-1
-2
数轴上的点有些表示有理数,有些表示无理数,所以数轴上的每一点都表示一个实数.
结论:实数与数轴上的点是一一对应的.
请将数轴上的各点与下列实数对应起来:
随堂练习
0
1
2
3
4
-1
-2
-3
A
B
C
D
E
, -1.5 , , 4
0
1
2
3
4
-1
-2
-3
试一试:
如图,观看数轴直接判断 的大小关系.
2和
2 ﹤
类比有理数在数轴上的分布规律,对于实数在数轴上如何分布,你有何启发?
结论:在数轴上表示的两个实数,左边的数总比 右边的数小.
类比有理数求相反数、绝对值,
对于如何求实数相反数、绝对值,
你有何启发?
1.a是一个实数,它的相反数为_______ ,
绝对值为_________;
在实数范围内,相反数、绝对值的意义和有理数范围内的相反数、绝对值的意义完全一样。
2.正实数的绝对值是__________,
0的绝对值是___________,
负实数的绝对值是____________.
它本身
0
它的相反数
结论:
随堂练习
今天我们学习了什么知识
★无理数和实数的概念以及实数的分类.
★实数与数轴上的点具有一一对应关系.
★实数范围内的相反数、绝对值的意义.
我们学习了:
★类比学习体现了数学中的类比思想.
知识拓展
试将下列所给的数进行分类,你能找到几种不同的分类
0,
-3.7,
-4,
3.14,
【友情提示】
(1)按有理数、无理数分类;
(2)按正数、负数、零分类;
(3)按绝对值是否大于1分类;
(4)按是否带根号分类;
(5)按是否整数分类等.
作业:
阅读书本P82-P85
作业本(2)
口答: 9的平方根是____________
9的算术平方根是________
2的平方根是____________
2的算术平方根是________
3
复习提问
±3
问题1: 3、-3都是有理数吗
问题2: 都是有理数吗
10.3 实数 (第一课时)
知识回顾
1、有理数的概念
整数和分数统称为有理数.
2、有理数的分类
有理数
分数
整数
正整数
0
负整数
正分数
负分数
有理数
正有理数
负有理数
0
正分数
正整数
负整数
负分数
探究一
借助计算器,把下列有理数写成小数的形式,你有什么发现?
5.875
3.0
- 0.6
·
2
1
0
.
任何一个有理数都可以写成有限小数或无限循环小数的形式.
反过来,任何有限小数或无限循环小数也都是有理数.
再使用计算器,把 写成小数的形式,你有什么发现?
我们把这种无限且不循环的小数叫做无理数.
1.41421356237309504880168…
公元前500年,古希腊毕达哥拉斯(Pythagoras)学派认为“万物皆为数”,即宇宙间的一切现象都能归结为整数与整数之比,也就是指一切现象都可用有理数来描述。
但后来这学派的成员希伯索斯(Hippasus) 发现边长为1的正方形的对角线的长不能用整数或整数之比来表示,这就动摇了毕达哥拉斯学派的信条,引起了信徒们的恐慌,据说,他为此被投入大海,为发现真理而献出宝贵的生命,但真理是不可战胜的。
你知道边长为1的正方形的对角线的长为多少吗?
1
4
2
1
A
D
C
B
E
F
M
N
1
1
2
2
除了 ,你能举出其他的一些无理数吗?
讨论:带根号的数都是无理数吗
说一说
有限小数或无限循环小数
无限不循环小数
有理数
无理数
练习:把下列各数分别填入相应的集合内
有理数集合
无理数集合
(相邻两个3之间
的7的个数逐次增加1个)
无理数也像有理数一样有正负之分.
无理数
正无理数
负无理数
(相邻两个3之间的7的个数逐次增加1个)
有理数和无理数统称为实数.
有理数
无理数
实数
初中阶段对数的认识范围扩充为
新加入
讨论交流:实数如何分类?
实数
有理数
正有理数
负有理数
零
无理数
正无理数
负无理数
或 有理数
整数
分数
实数
正实数
0
负实数
正有理数
正无理数
负有理数
负无理数
随堂练习
判断:
⑴实数不是有理数就是无理数。( )
⑵无理数都是无限不循环小数。( )
⑶无理数都是无限小数。( )
⑷带根号的数都是无理数。( )
⑸无理数一定都带根号。( )
⑹两个无理数之积不一定是无理数。( )
⑺两个无理数之和一定是无理数。( )
⑻数轴上的任何一点都可以表示实数。( )
×
×
×
如下图,以单位长度为边长画一个正方形,以原点为圆心,正方形对角线为半径画弧,与正、负半轴的交点分别为点A和点B,数轴上A点和B点对应的数是什么?
-2
-1
0
1
2
B
A
C
探究:每个有理数都可以用数轴上的点来表示.
无理数是否也可以用数轴上的点来表示出来呢
问题一:
无理数 可以用数轴上的点来表示出来.
OA的长是这个圆的周长 ,所以点A的坐标是
探究:每个有理数都可以用数轴上的点来表示.
无理数是否也可以用数轴上的点来表示出来呢
无理数 可以用数轴上的点来表示出来.
问题二:如图,直径为1个单位长度的圆从原点沿数轴向右滚动一周,圆上一点从原点到达A点,则点A的坐标为多少?
-4
-2
0
1
2
3
4
-1
-3
A
除了 ,其实所有的无理数都可以在数轴上表示出来,所以实数都可以在数轴上表示出来.
探究:每个有理数都可以用数轴上的点来表示.
无理数是否也可以用数轴上的点来表示出来呢
0
1
2
3
-1
-2
数轴上的点有些表示有理数,有些表示无理数,所以数轴上的每一点都表示一个实数.
结论:实数与数轴上的点是一一对应的.
请将数轴上的各点与下列实数对应起来:
随堂练习
0
1
2
3
4
-1
-2
-3
A
B
C
D
E
, -1.5 , , 4
0
1
2
3
4
-1
-2
-3
试一试:
如图,观看数轴直接判断 的大小关系.
2和
2 ﹤
类比有理数在数轴上的分布规律,对于实数在数轴上如何分布,你有何启发?
结论:在数轴上表示的两个实数,左边的数总比 右边的数小.
类比有理数求相反数、绝对值,
对于如何求实数相反数、绝对值,
你有何启发?
1.a是一个实数,它的相反数为_______ ,
绝对值为_________;
在实数范围内,相反数、绝对值的意义和有理数范围内的相反数、绝对值的意义完全一样。
2.正实数的绝对值是__________,
0的绝对值是___________,
负实数的绝对值是____________.
它本身
0
它的相反数
结论:
随堂练习
今天我们学习了什么知识
★无理数和实数的概念以及实数的分类.
★实数与数轴上的点具有一一对应关系.
★实数范围内的相反数、绝对值的意义.
我们学习了:
★类比学习体现了数学中的类比思想.
知识拓展
试将下列所给的数进行分类,你能找到几种不同的分类
0,
-3.7,
-4,
3.14,
【友情提示】
(1)按有理数、无理数分类;
(2)按正数、负数、零分类;
(3)按绝对值是否大于1分类;
(4)按是否带根号分类;
(5)按是否整数分类等.
作业:
阅读书本P82-P85
作业本(2)
