10.3.1实数(1)
图片预览






文档简介
(共20张PPT)
毕达哥拉斯(Pythagoras,约公元前580——前500年),古希腊数学家,毕达哥斯学派的主要代表人物.
数学小史
同学们,你们赞成这位数学家的说法吗?
这是古希腊著名的数学家毕达哥拉斯,他在意大利南部的克罗托那建立了一个秘密组织,形成了“毕达哥拉斯学派”,这个学派对数学发展有重要的贡献,著名的勾股定理就是这个学派智慧的结晶.
毕达哥拉斯说:“世界上只有整数和分数,除此之外就再也没有什么别的数了!”
有理数
整数
分数
有理数
正有理数
零
负有理数
回顾
有理数包括哪些数?
3,
,
3
5
,
47
8
,
11
9
,
11
9
.
5
9
像
使用计算器计算,把下列有理数写成小数的形式,你有什么发现?
3 = 3.0,
= 0.6,
3
5
47
8
= 5.875,
11
9
= 0.81,
.
.
= 0.5.
5
9
.
= 0.12,
11
9
.
★任何一个有理数都可以写成有限小数或无限循环小数的形式.
探究
除了有限小数和无限循环小数,还有其它类型的小数吗?
叫做无理数.
新知
所有的数都可以写成有限小数和无限循环小数的形式吗?
=1.41421356237309504880168…
=1.73205080756887729352744…
π=3.1415926535897932384626…
1.010010001…
(两个1之间依次多一个0)
无限不循环小数
无理数的概念
无理数也有正负之分,
正无理数:
负无理数:
例如:
,
,
…
—
—
—
,
,
…
无理数的分类
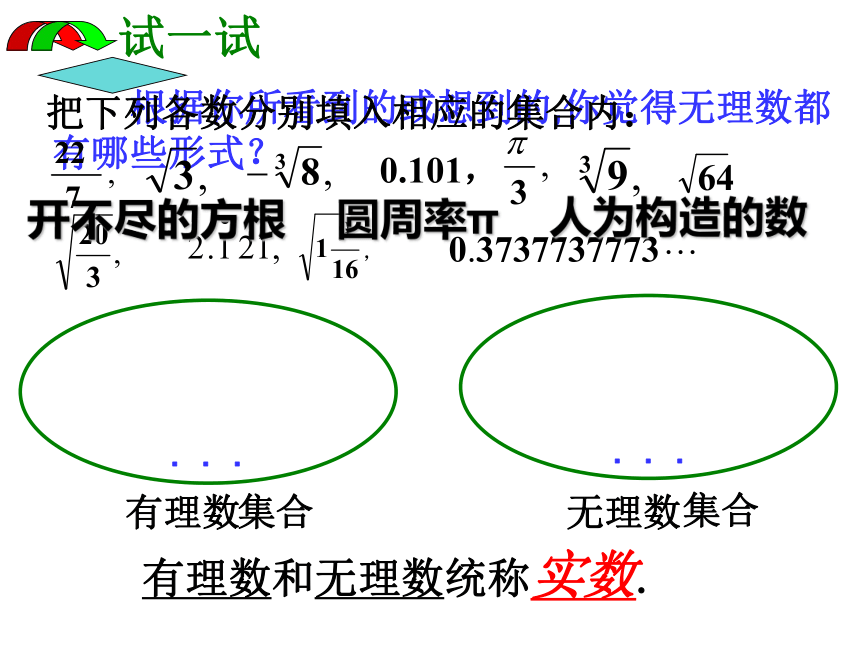
根据你所看到的或想到的,你觉得无理数都有哪些形式?
试一试
把下列各数分别填入相应的集合内:
0.101,
,
有理数
无理数
集合
集合
有理数和无理数统称实数.
...
...
圆周率π
开不尽的方根
人为构造的数
有理数
无理数
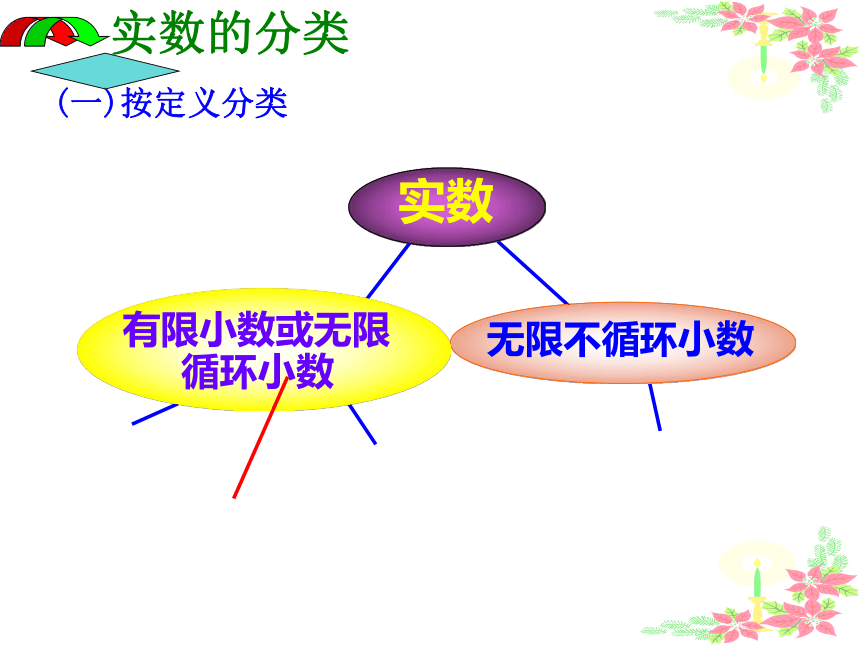
(一)按定义分类
分数
整数
实数
无限不循环小数
有限小数或无限
循环小数
实数的分类
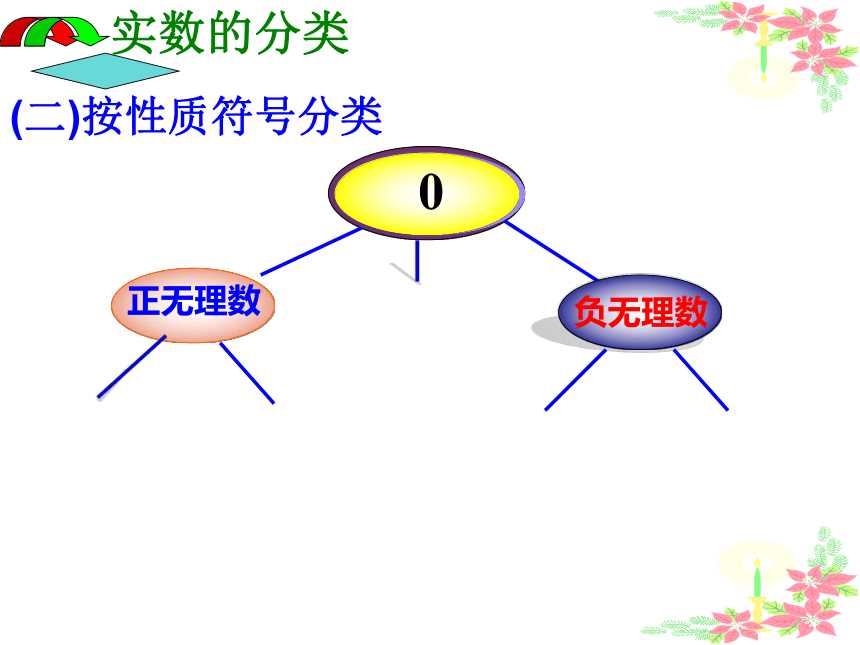
(二)按性质符号分类
实数
正实数
负实数
0
正有理数
正无理数
负有理数
负无理数
实数的分类
练一练
1.判断:
(1)实数不是有理数就是无理数;( )
(2)无理数都是无限不循环小数;( )
(3)无理数都是无限小数; ( )
(4)带根号的数都是无理数; ( )
(5)无理数一定都带根号. ( )
×
×
2. 把下列各数填入相应的集合内:
(1)有理数集合:
(2)无理数集合:
(3)整数集合:
(4)负数集合:
(5)分数集合:
(6)实数集合:
练一练
练一练
当数从有理数扩充到实数以后,有理数关于相反数和绝对值的意义同样适合于实数.
探究
如图,直径为1个单位长度的圆从原点沿数轴向右滚动一周,圆上一点从原点到达A点,则点A的坐标为多少?
-4
-2
0
1
2
3
4
-1
-3
无理数 可以用数轴上的点来表示.
A
问题2.你能在数轴上表示出 吗?
问题1.无理数能在数轴上表示出来吗?
探究
探究
-2
-1
0
1
2
-
每一个实数都可以用数轴上的一个点来表示;
反过来,数轴上的每一点都表示一个实数。
★实数和数轴上的点是一一对应的.
探究
问题3.能在直角坐标系中描示出点( ,1)吗?
( ,1)
有序实数对
有序实数对和直角坐标系中的点是一一对应的.
-2
-1
0
1
2
-1
1
x
y
知识拓展
试将下列所有数进行分类,你能找到几种不同的分类
0,
-3.7,
-4,
3.14,
【友情提示】
(1)按有理数、无理数分类;
(2)按正数、负数、零分类;
(3)按绝对值是否大于1分类;
(4)按是否带根号分类;
(5)按是否整数分类等.
…
实数
课堂小结
…
有理数
…
无理数
★实数和数轴上的点是一一对应的.
★有序实数对和直角坐标系中的点是一 一对应的.
原创与经典B:P32-33
阅读与思考课本P88的材料
《为什么说 不是有理数》
再见
毕达哥拉斯(Pythagoras,约公元前580——前500年),古希腊数学家,毕达哥斯学派的主要代表人物.
数学小史
同学们,你们赞成这位数学家的说法吗?
这是古希腊著名的数学家毕达哥拉斯,他在意大利南部的克罗托那建立了一个秘密组织,形成了“毕达哥拉斯学派”,这个学派对数学发展有重要的贡献,著名的勾股定理就是这个学派智慧的结晶.
毕达哥拉斯说:“世界上只有整数和分数,除此之外就再也没有什么别的数了!”
有理数
整数
分数
有理数
正有理数
零
负有理数
回顾
有理数包括哪些数?
3,
,
3
5
,
47
8
,
11
9
,
11
9
.
5
9
像
使用计算器计算,把下列有理数写成小数的形式,你有什么发现?
3 = 3.0,
= 0.6,
3
5
47
8
= 5.875,
11
9
= 0.81,
.
.
= 0.5.
5
9
.
= 0.12,
11
9
.
★任何一个有理数都可以写成有限小数或无限循环小数的形式.
探究
除了有限小数和无限循环小数,还有其它类型的小数吗?
叫做无理数.
新知
所有的数都可以写成有限小数和无限循环小数的形式吗?
=1.41421356237309504880168…
=1.73205080756887729352744…
π=3.1415926535897932384626…
1.010010001…
(两个1之间依次多一个0)
无限不循环小数
无理数的概念
无理数也有正负之分,
正无理数:
负无理数:
例如:
,
,
…
—
—
—
,
,
…
无理数的分类
根据你所看到的或想到的,你觉得无理数都有哪些形式?
试一试
把下列各数分别填入相应的集合内:
0.101,
,
有理数
无理数
集合
集合
有理数和无理数统称实数.
...
...
圆周率π
开不尽的方根
人为构造的数
有理数
无理数
(一)按定义分类
分数
整数
实数
无限不循环小数
有限小数或无限
循环小数
实数的分类
(二)按性质符号分类
实数
正实数
负实数
0
正有理数
正无理数
负有理数
负无理数
实数的分类
练一练
1.判断:
(1)实数不是有理数就是无理数;( )
(2)无理数都是无限不循环小数;( )
(3)无理数都是无限小数; ( )
(4)带根号的数都是无理数; ( )
(5)无理数一定都带根号. ( )
×
×
2. 把下列各数填入相应的集合内:
(1)有理数集合:
(2)无理数集合:
(3)整数集合:
(4)负数集合:
(5)分数集合:
(6)实数集合:
练一练
练一练
当数从有理数扩充到实数以后,有理数关于相反数和绝对值的意义同样适合于实数.
探究
如图,直径为1个单位长度的圆从原点沿数轴向右滚动一周,圆上一点从原点到达A点,则点A的坐标为多少?
-4
-2
0
1
2
3
4
-1
-3
无理数 可以用数轴上的点来表示.
A
问题2.你能在数轴上表示出 吗?
问题1.无理数能在数轴上表示出来吗?
探究
探究
-2
-1
0
1
2
-
每一个实数都可以用数轴上的一个点来表示;
反过来,数轴上的每一点都表示一个实数。
★实数和数轴上的点是一一对应的.
探究
问题3.能在直角坐标系中描示出点( ,1)吗?
( ,1)
有序实数对
有序实数对和直角坐标系中的点是一一对应的.
-2
-1
0
1
2
-1
1
x
y
知识拓展
试将下列所有数进行分类,你能找到几种不同的分类
0,
-3.7,
-4,
3.14,
【友情提示】
(1)按有理数、无理数分类;
(2)按正数、负数、零分类;
(3)按绝对值是否大于1分类;
(4)按是否带根号分类;
(5)按是否整数分类等.
…
实数
课堂小结
…
有理数
…
无理数
★实数和数轴上的点是一一对应的.
★有序实数对和直角坐标系中的点是一 一对应的.
原创与经典B:P32-33
阅读与思考课本P88的材料
《为什么说 不是有理数》
再见
