完全平方公式(1)
图片预览





文档简介
(共14张PPT)
沙市实验中学
数学教研组
(a+b)(m+n)
=
am
复习:多项式的乘法法则
+an
+bm
+bn
多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.
探究
计算下列各式,你能发现什么规律
(p+2)2 = (p+2) (p+2) = ______
(m+2)2= _________;
(p-1)2 = (p-1 ) (p-1) = ________;
(m-2)2 = __________.
P2+4p+4
m2+4m+4
P2-2p+1
m2-4m+4
计算:(a+b)2 和 (a-b)2.
(a+b)2=(a+b) (a+b) = a2+ab+ab+b2
=a2+2ab+b2.
(a-b)2 = (a-b) (a-b) = a2-ab-ab+b2
=a2-2ab+b2
完全平方公式的数学表达式:
完全平方公式的文字叙述:
两个数的和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的2倍。
(a+b)2= a2 +b2 +2ab
(a-b)2= a2 +b2 - 2ab
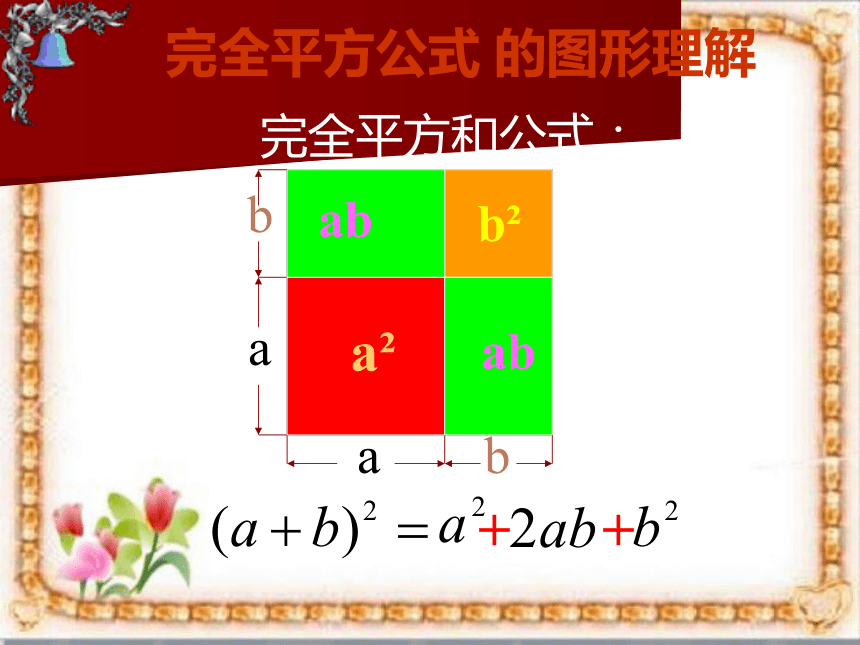
(a+b)2= a2 +2ab+b2
(a-b)2= a2 - 2ab+b2
b
b
a
a
(a+b)
a
b
ab
ab
+
+
完全平方和公式:
完全平方公式 的图形理解
公式特点:
4、公式中的字母a,b可以表示数,单项式和
多项式。
(a+b)2= a2 +2ab+b2
(a-b)2= a2 - 2ab+b2
1、积为二次三项式;
2、积中两项为两数的平方和;
3、另一项是两数积的2倍,且与乘式中间 的符号相同。
首平方,末平方,首末两倍中间放,符号与前一个样
下面各式的计算是否正确?如果不正确,应当怎样改正?
(x+y)2=x2 +y2
(2)(x -y)2 =x2 -y2
(3) (-x +y)2 =x2+2xy +y2
(4) (2x+y)2 =4x2 +2xy +y2
错
错
错
错
(x +y)2 =x2+2xy +y2
(x -y)2 =x2 -2xy +y2
(-x + y)2 =x2 -2xy +y2
(2x +y)2 =4x2+4xy +y2
例1 运用完全平方公式计算:
解: (4m-n)2=
=16m2
(1)(4m-n)2
(a +b)2= a2 + 2 ab + b2
(4m)2
-2 (4m) n
+n2
-8mn
+n2
运用完全平方公式计算:
(1) 1022
解: 1022
= (100+2)2
=10000+400+4
=10404
(2) 992
解: 992
= (100 –1)2
=10000 -200+1
=9801
小结:
(a+b)2= a2 +2ab+b2
(a-b)2= a2 - 2ab+b2
1、完全平方公式:
2、注意:项数、符号、字母及其指数;
3、解题时常用结论:
(-a-b)2 =(a+b)2 (a-b)2 =(b-a)2
沙市实验中学
数学教研组
(a+b)(m+n)
=
am
复习:多项式的乘法法则
+an
+bm
+bn
多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.
探究
计算下列各式,你能发现什么规律
(p+2)2 = (p+2) (p+2) = ______
(m+2)2= _________;
(p-1)2 = (p-1 ) (p-1) = ________;
(m-2)2 = __________.
P2+4p+4
m2+4m+4
P2-2p+1
m2-4m+4
计算:(a+b)2 和 (a-b)2.
(a+b)2=(a+b) (a+b) = a2+ab+ab+b2
=a2+2ab+b2.
(a-b)2 = (a-b) (a-b) = a2-ab-ab+b2
=a2-2ab+b2
完全平方公式的数学表达式:
完全平方公式的文字叙述:
两个数的和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的2倍。
(a+b)2= a2 +b2 +2ab
(a-b)2= a2 +b2 - 2ab
(a+b)2= a2 +2ab+b2
(a-b)2= a2 - 2ab+b2
b
b
a
a
(a+b)
a
b
ab
ab
+
+
完全平方和公式:
完全平方公式 的图形理解
公式特点:
4、公式中的字母a,b可以表示数,单项式和
多项式。
(a+b)2= a2 +2ab+b2
(a-b)2= a2 - 2ab+b2
1、积为二次三项式;
2、积中两项为两数的平方和;
3、另一项是两数积的2倍,且与乘式中间 的符号相同。
首平方,末平方,首末两倍中间放,符号与前一个样
下面各式的计算是否正确?如果不正确,应当怎样改正?
(x+y)2=x2 +y2
(2)(x -y)2 =x2 -y2
(3) (-x +y)2 =x2+2xy +y2
(4) (2x+y)2 =4x2 +2xy +y2
错
错
错
错
(x +y)2 =x2+2xy +y2
(x -y)2 =x2 -2xy +y2
(-x + y)2 =x2 -2xy +y2
(2x +y)2 =4x2+4xy +y2
例1 运用完全平方公式计算:
解: (4m-n)2=
=16m2
(1)(4m-n)2
(a +b)2= a2 + 2 ab + b2
(4m)2
-2 (4m) n
+n2
-8mn
+n2
运用完全平方公式计算:
(1) 1022
解: 1022
= (100+2)2
=10000+400+4
=10404
(2) 992
解: 992
= (100 –1)2
=10000 -200+1
=9801
小结:
(a+b)2= a2 +2ab+b2
(a-b)2= a2 - 2ab+b2
1、完全平方公式:
2、注意:项数、符号、字母及其指数;
3、解题时常用结论:
(-a-b)2 =(a+b)2 (a-b)2 =(b-a)2
