第14章 14.2勾股定理的应用 同步练习
文档属性
| 名称 | 第14章 14.2勾股定理的应用 同步练习 |

|
|
| 格式 | doc | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-11 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
初中数学华师大版八年级上学期 第14章 14.2勾股定理的应用
一、单选题
1.我国古代数学著作《九章算术》记载了一道有趣的问题.原文是:今有池方一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐.问水深、葭长各几何.译为:有一个水池,水面是一个边长为10尺的正方形,在水池正中央有一根芦苇,它高出水面1尺,如果把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面,水的深度与这根芦苇的长度分别是多少?设芦苇的长度是 尺.根据题意,可列方程为(?? )
A.???????????B.???????????C.???????????D.?
第1题 第2题 第3题
2.如图,斜靠在墙上的一根竹竿,AB=5m,OB=3m。若B端沿地面OB方向外移0.5m,则A端沿垂直于地面AC方向下移(??? ) 21世纪教育网版权所有
A.?等于0.5m????????????????????????????B.?小于0.5m????????????????????????????C.?大于0.5m????????????????????????????D.?不确定
3.如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为 ,则正方形A,B,C,D的面积之和为( ) 21cnjy.com
A.?????????????????????????????????B.?????????????????????????????????C.?????????????????????????????????D.?
4.在我国古代数学_è?????????????????_术》的第九章《勾股》中记载了这样一个问题:“今天有开门去阔一尺,不合二寸,问门广几何?”意思是:如图,推开两扇门(AD和BC),门边缘D,C两点到门槛AB的距离是1尺,两扇门的间隙CD为2寸,则门宽AB长是(??? )寸(1尺=10寸) 21·cn·jy·com
A.?101???????????????????????????????????????B.?100???????????????????????????????????????C.?52???????????????????????????????????????D.?96
第4题 第5题 第6题
5.如图,在直角三角形ABC中,∠B=90°,AB=CB,则以下式子一定成立的是(??? )
A.?a2+b2=c2???????????????????????B.?(a+c)2=b2???????????????????????C.?(a+b)(a-b)=c2???????????????????????D.?b2=2a2
6.在正方形网格中,每个小正方形的边长均为 ,点 是格点上的点,把点 先向右移动 格,再向下移动 格到点 ,那么 两点的距离是(? ) www.21-cn-jy.com
A.??????????????????????????????????????????B.??????????????????????????????????????????C.??????????????????????????????????????????D.?
二、填空题
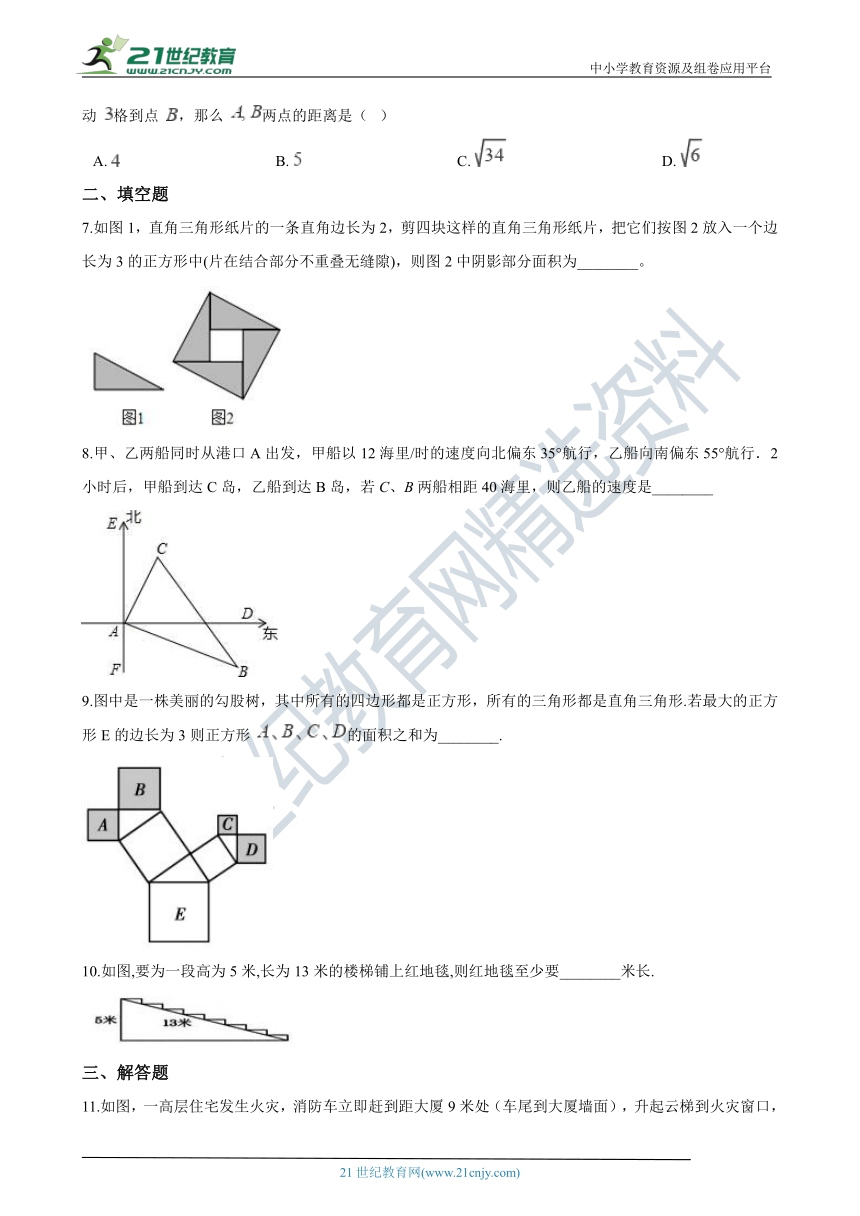
7.如图1,直角三角形_??????????????????_角边长为2,剪四块这样的直角三角形纸片,把它们按图2放入一个边长为3的正方形中(片在结合部分不重叠无缝隙),则图2中阴影部分面积为________。
8.甲、乙两船同时从_??????A?????????_甲船以12海里/时的速度向北偏东35°航行,乙船向南偏东55°航行.2小时后,甲船到达C岛,乙船到达B岛,若C、B两船相距40海里,则乙船的速度是________
9.图中是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若最大的正方形E的边长为3则正方形 的面积之和为________. 2·1·c·n·j·y
10.如图,要为一段高为5米,长为13米的楼梯铺上红地毯,则红地毯至少要________米长.
?
三、解答题
11.如图,一高层住宅发生火_?????????é??è?????_即赶到距大厦9米处(车尾到大厦墙面),升起云梯到火灾窗口,已知云梯长15米,云梯底部距地面2米,问:发生火灾的住户窗口距离地面多高?
12.如图,一棵小树在大风中被吹歪,用一根棍子把小树扶直,已知支撑点到地面的距离是 米,棍子的长度为5.5米,求棍子和地面接触点 到小树底部 的距离是多少? 【来源:21·世纪·教育·网】
13.如图,某电信公_???è???????¨A???_B两乡镇间的E处修建一座5G信号塔,且使C,D两个村庄到E的距离相等.已知AD⊥AB于点A,BC⊥AB于点B,AB=80km,AD=50km,BC=30km,求5G信号塔E应该建在离A乡镇多少千米的地方? 21·世纪*教育网
14.一艘轮船以_20??·é??/???_的速度由西向东航行,在途中接到台风警报,台风中心正以40海里/时的速度由南向北移动,距台风中心20海里的圆形区域(包括边界)都属于台风区域,当轮船到A处时测得台风中心移到位于点A正南方的B处,且AB=100海里.若这艘轮船自A处按原速度继续航行,在途中是否会遇到台风?若会,则求出轮船最初遇到台风的时间;若不会,请说明理由. www-2-1-cnjy-com
四、综合题
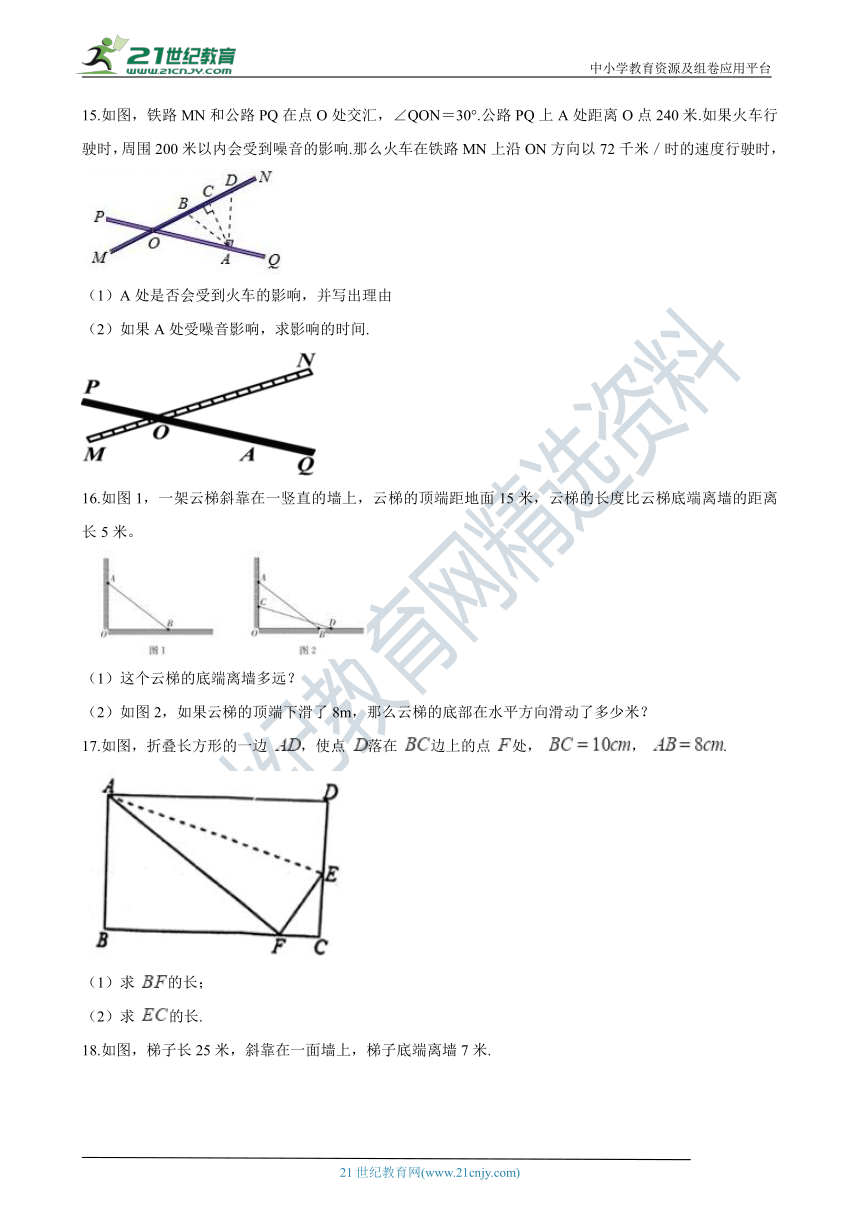
15.如图,铁_è·?MN??????è·?_PQ在点O处交汇,∠QON=30°.公路PQ上A处距离O点240米.如果火车行驶时,周围200米以内会受到噪音的影响.那么火车在铁路MN上沿ON方向以72千米/时的速度行驶时,
(1)A处是否会受到火车的影响,并写出理由
(2)如果A处受噪音影响,求影响的时间.
16.如图1,一架云梯斜靠在一竖直的墙上,云梯的顶端距地面15米,云梯的长度比云梯底端离墙的距离长5米。 21教育网
(1)这个云梯的底端离墙多远?
(2)如图2,如果云梯的顶端下滑了8m,那么云梯的底部在水平方向滑动了多少米?
17.如图,折叠长方形的一边 ,使点 落在 边上的点 处, , .
(1)求 的长;
(2)求 的长.
18.如图,梯子长25米,斜靠在一面墙上,梯子底端离墙7米.
(1)这个梯子的顶端距地面有多高?
(2)如果梯子的顶端下滑了4米,那么梯子的底端在水平方向滑动了几米?
答案部分
一、单选题
1. B
2. B
3. D
4. A
5. D
6. C
二、填空题
7.
8. 16海里/时
9. 9
10. 18
三、解答题
11. 解:由题意,AB=15,AC=DE=9,CD=AE=2,BD⊥AC,
在Rt△ACB中,由勾股定理得:
,
∴BD=BC+CD=14(米),
答:发生火灾的住户窗口距离地面14米.
12. 由题意知:AB= 米,AC=5.5米,
∵∠ABC=90°,
∴ =4.5米,
13. 解:设AE=xkm,则BE=(80-x)km
∵AD⊥AB,BC⊥AB
∴ 和△BCE都是直角三角形
∴ ,
又∵AD=50,BC=30,DE=CE
∴ .
解得
答:5G信号塔E应该建在离A乡镇多30千米的地方.
14. 解:不会受影响,
假设途中会遇到台风,且最初遇到的时间为th,此时轮船位于C处,台风中心移到E处,连接CE,
则AC=20t,
AE=AB﹣BE=100﹣40t,
AC2+AE2=EC2 .
(20t)2+(100﹣40t)2=202 ,
整理得:5t2﹣20t+24=0
∵△=(﹣20)2﹣4×5×24<0
∴方程无实数根,
∴不会受影响.
四、综合题
15. (1)如图,过点A作AC⊥ON,AB=AD=200米,
∵∠QON=30°,OA=240米,
∴AC=120米<200,故受到火车的影响,
(2)当火车到B点时开始对A处有噪音影响,此时AB=200,
∵AB=200,AC=120,
利用勾股定理得出BC=160,同理CD=160.即BD=320米,
∴影响的时间为 秒.
16. (1)解:根据题意可得OA=15米,AB-OB=5米。
由勾股定理可得OA2+OB2=AB2 , 即152+OB2=(5+OB)2 ,
解得OB=20米.
答:这个云梯的底端离墙20米。
(2)解:由(1)可得AB=20+5=25米,
根据题意可得CO=7米,CD=AB=25米,
由勾股定理可得OC2+OD2=CD2 , 即OD= =24,
∴BD=24-20=4米。
答:云梯的底部在水平方向滑动了4米。
17. (1)解:由题意可得,
在 中,∵ ,
∴
(2)解:∵
由题意可得 ,设 的长为 cm
则在 中,
解得
则 的长为
18. (1)解:根据题意得 ,
∴梯子顶端距地面的高度 米
(2)解: = 米,
∵
∴根据勾股定理得, 米,
∴ 米,
答:梯子下端滑行了8米.
_21?????????è?????(www.21cnjy.com)_
初中数学华师大版八年级上学期 第14章 14.2勾股定理的应用
一、单选题
1.我国古代数学著作《九章算术》记载了一道有趣的问题.原文是:今有池方一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐.问水深、葭长各几何.译为:有一个水池,水面是一个边长为10尺的正方形,在水池正中央有一根芦苇,它高出水面1尺,如果把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面,水的深度与这根芦苇的长度分别是多少?设芦苇的长度是 尺.根据题意,可列方程为(?? )
A.???????????B.???????????C.???????????D.?
第1题 第2题 第3题
2.如图,斜靠在墙上的一根竹竿,AB=5m,OB=3m。若B端沿地面OB方向外移0.5m,则A端沿垂直于地面AC方向下移(??? ) 21世纪教育网版权所有
A.?等于0.5m????????????????????????????B.?小于0.5m????????????????????????????C.?大于0.5m????????????????????????????D.?不确定
3.如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为 ,则正方形A,B,C,D的面积之和为( ) 21cnjy.com
A.?????????????????????????????????B.?????????????????????????????????C.?????????????????????????????????D.?
4.在我国古代数学_è?????????????????_术》的第九章《勾股》中记载了这样一个问题:“今天有开门去阔一尺,不合二寸,问门广几何?”意思是:如图,推开两扇门(AD和BC),门边缘D,C两点到门槛AB的距离是1尺,两扇门的间隙CD为2寸,则门宽AB长是(??? )寸(1尺=10寸) 21·cn·jy·com
A.?101???????????????????????????????????????B.?100???????????????????????????????????????C.?52???????????????????????????????????????D.?96
第4题 第5题 第6题
5.如图,在直角三角形ABC中,∠B=90°,AB=CB,则以下式子一定成立的是(??? )
A.?a2+b2=c2???????????????????????B.?(a+c)2=b2???????????????????????C.?(a+b)(a-b)=c2???????????????????????D.?b2=2a2
6.在正方形网格中,每个小正方形的边长均为 ,点 是格点上的点,把点 先向右移动 格,再向下移动 格到点 ,那么 两点的距离是(? ) www.21-cn-jy.com
A.??????????????????????????????????????????B.??????????????????????????????????????????C.??????????????????????????????????????????D.?
二、填空题
7.如图1,直角三角形_??????????????????_角边长为2,剪四块这样的直角三角形纸片,把它们按图2放入一个边长为3的正方形中(片在结合部分不重叠无缝隙),则图2中阴影部分面积为________。
8.甲、乙两船同时从_??????A?????????_甲船以12海里/时的速度向北偏东35°航行,乙船向南偏东55°航行.2小时后,甲船到达C岛,乙船到达B岛,若C、B两船相距40海里,则乙船的速度是________
9.图中是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若最大的正方形E的边长为3则正方形 的面积之和为________. 2·1·c·n·j·y
10.如图,要为一段高为5米,长为13米的楼梯铺上红地毯,则红地毯至少要________米长.
?
三、解答题
11.如图,一高层住宅发生火_?????????é??è?????_即赶到距大厦9米处(车尾到大厦墙面),升起云梯到火灾窗口,已知云梯长15米,云梯底部距地面2米,问:发生火灾的住户窗口距离地面多高?
12.如图,一棵小树在大风中被吹歪,用一根棍子把小树扶直,已知支撑点到地面的距离是 米,棍子的长度为5.5米,求棍子和地面接触点 到小树底部 的距离是多少? 【来源:21·世纪·教育·网】
13.如图,某电信公_???è???????¨A???_B两乡镇间的E处修建一座5G信号塔,且使C,D两个村庄到E的距离相等.已知AD⊥AB于点A,BC⊥AB于点B,AB=80km,AD=50km,BC=30km,求5G信号塔E应该建在离A乡镇多少千米的地方? 21·世纪*教育网
14.一艘轮船以_20??·é??/???_的速度由西向东航行,在途中接到台风警报,台风中心正以40海里/时的速度由南向北移动,距台风中心20海里的圆形区域(包括边界)都属于台风区域,当轮船到A处时测得台风中心移到位于点A正南方的B处,且AB=100海里.若这艘轮船自A处按原速度继续航行,在途中是否会遇到台风?若会,则求出轮船最初遇到台风的时间;若不会,请说明理由. www-2-1-cnjy-com
四、综合题
15.如图,铁_è·?MN??????è·?_PQ在点O处交汇,∠QON=30°.公路PQ上A处距离O点240米.如果火车行驶时,周围200米以内会受到噪音的影响.那么火车在铁路MN上沿ON方向以72千米/时的速度行驶时,
(1)A处是否会受到火车的影响,并写出理由
(2)如果A处受噪音影响,求影响的时间.
16.如图1,一架云梯斜靠在一竖直的墙上,云梯的顶端距地面15米,云梯的长度比云梯底端离墙的距离长5米。 21教育网
(1)这个云梯的底端离墙多远?
(2)如图2,如果云梯的顶端下滑了8m,那么云梯的底部在水平方向滑动了多少米?
17.如图,折叠长方形的一边 ,使点 落在 边上的点 处, , .
(1)求 的长;
(2)求 的长.
18.如图,梯子长25米,斜靠在一面墙上,梯子底端离墙7米.
(1)这个梯子的顶端距地面有多高?
(2)如果梯子的顶端下滑了4米,那么梯子的底端在水平方向滑动了几米?
答案部分
一、单选题
1. B
2. B
3. D
4. A
5. D
6. C
二、填空题
7.
8. 16海里/时
9. 9
10. 18
三、解答题
11. 解:由题意,AB=15,AC=DE=9,CD=AE=2,BD⊥AC,
在Rt△ACB中,由勾股定理得:
,
∴BD=BC+CD=14(米),
答:发生火灾的住户窗口距离地面14米.
12. 由题意知:AB= 米,AC=5.5米,
∵∠ABC=90°,
∴ =4.5米,
13. 解:设AE=xkm,则BE=(80-x)km
∵AD⊥AB,BC⊥AB
∴ 和△BCE都是直角三角形
∴ ,
又∵AD=50,BC=30,DE=CE
∴ .
解得
答:5G信号塔E应该建在离A乡镇多30千米的地方.
14. 解:不会受影响,
假设途中会遇到台风,且最初遇到的时间为th,此时轮船位于C处,台风中心移到E处,连接CE,
则AC=20t,
AE=AB﹣BE=100﹣40t,
AC2+AE2=EC2 .
(20t)2+(100﹣40t)2=202 ,
整理得:5t2﹣20t+24=0
∵△=(﹣20)2﹣4×5×24<0
∴方程无实数根,
∴不会受影响.
四、综合题
15. (1)如图,过点A作AC⊥ON,AB=AD=200米,
∵∠QON=30°,OA=240米,
∴AC=120米<200,故受到火车的影响,
(2)当火车到B点时开始对A处有噪音影响,此时AB=200,
∵AB=200,AC=120,
利用勾股定理得出BC=160,同理CD=160.即BD=320米,
∴影响的时间为 秒.
16. (1)解:根据题意可得OA=15米,AB-OB=5米。
由勾股定理可得OA2+OB2=AB2 , 即152+OB2=(5+OB)2 ,
解得OB=20米.
答:这个云梯的底端离墙20米。
(2)解:由(1)可得AB=20+5=25米,
根据题意可得CO=7米,CD=AB=25米,
由勾股定理可得OC2+OD2=CD2 , 即OD= =24,
∴BD=24-20=4米。
答:云梯的底部在水平方向滑动了4米。
17. (1)解:由题意可得,
在 中,∵ ,
∴
(2)解:∵
由题意可得 ,设 的长为 cm
则在 中,
解得
则 的长为
18. (1)解:根据题意得 ,
∴梯子顶端距地面的高度 米
(2)解: = 米,
∵
∴根据勾股定理得, 米,
∴ 米,
答:梯子下端滑行了8米.
_21?????????è?????(www.21cnjy.com)_
