华东师大版九年级下册:27.2.2直线和圆的位置关系 学案(无答案)
文档属性
| 名称 | 华东师大版九年级下册:27.2.2直线和圆的位置关系 学案(无答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 146.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-12 00:00:00 | ||
图片预览


文档简介
27.2.2直线和圆的位置关系
执笔:郭玉闯
审核:余亚丽
学习目标:1、理解圆与直线的位置关系
2、根据直线与圆的公共点的个数或圆心到直线的距离与圆的半径之间的数量关系判断直线与圆的位置关系
3、了解切线的概念,探索切线与过切点的半径之间关系,掌握切线的识别方法
学习重点:直线与圆的三种位置关系及圆的切线的判定。
学习难点:直线与圆的三种位置关系及圆的切线的性质与判定。
学习过程:
一、知识回顾:1、
叫两点间的距离
2、
叫点到直线的距离
二、探索新知:
知识点一:
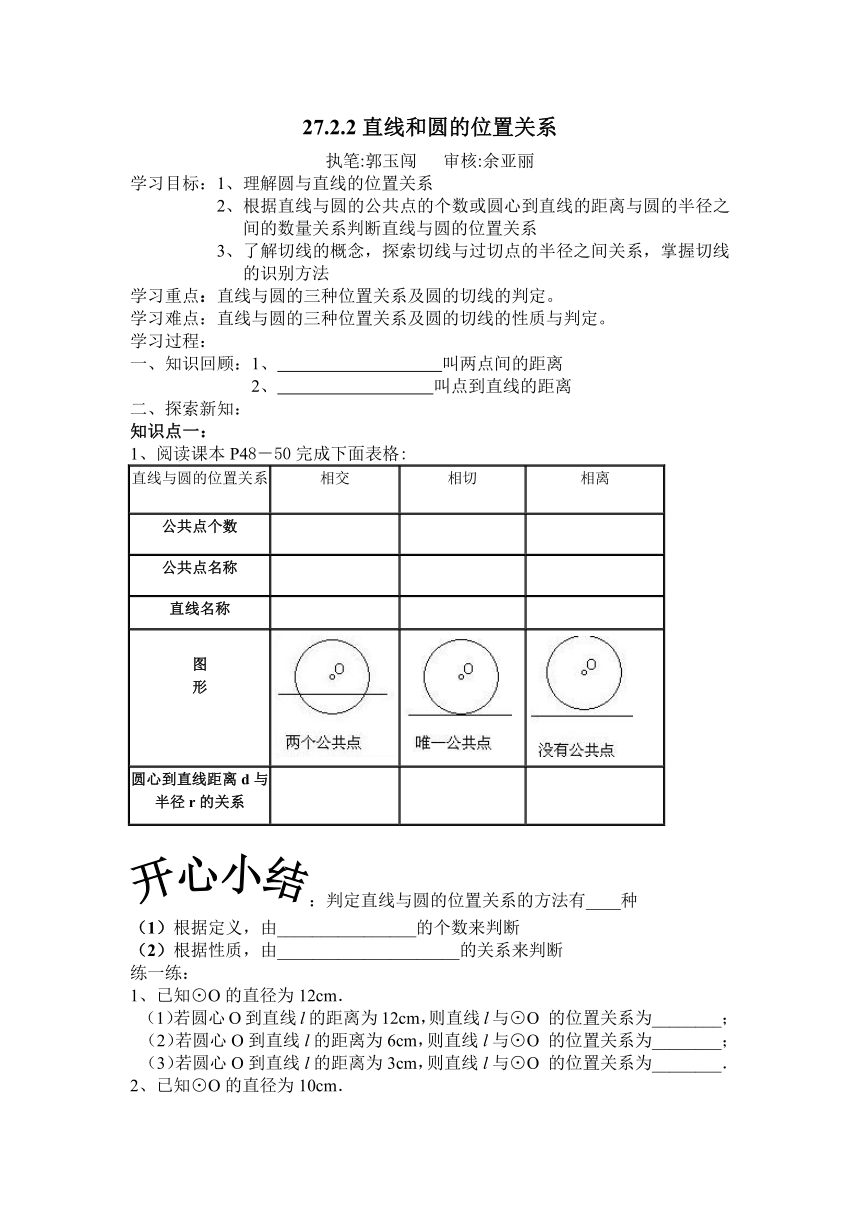
1、阅读课本P48-50完成下面表格:
直线与圆的位置关系
相交
相切
相离
公共点个数
公共点名称
?
直线名称
?
图
形
?
?
?
圆心到直线距离d与半径r的关系
?
?
?
:判定直线与圆的位置关系的方法有____种
(1)根据定义,由________________的个数来判断
(2)根据性质,由_____________________的关系来判断
练一练:
1、已知⊙O的直径为12cm.
(1)若圆心O到直线l的距离为12cm,则直线l与⊙O
的位置关系为________;
(2)若圆心O到直线l的距离为6cm,则直线l与⊙O
的位置关系为________;
(3)若圆心O到直线l的距离为3cm,则直线l与⊙O
的位置关系为________.
2、已知⊙O的直径为10cm.
(1)若直线l与⊙O相交,则圆心O到直线l的距离为________;
(2)若直线l与⊙O相切,则圆心O到直线l的距离为________;
(3)若直线l与⊙O相离,则圆心O到直线l的距离为________
1、已知圆的直径为10,直线与圆心的距离为4,那么圆和直线有
个公共点。
2、⊙O的半径为,圆心O到直线的距离为,如果=4,=4,那么直线与⊙O的位置关系是
,如果5=3,那么直线与⊙O的位置关系是
。
3、△ABC中,∠C=90°,AC=3,AB=5,以C为圆心,为半径作⊙C,则直线AB与⊙C相离时,的取值范围是
;相切时,的取值范围是取值范围是
;相交时的取值范围是
。⊙C与线段AB相交时,r的取值范围是
。
4、Rt△ABC的斜边AB=4,直角边AC=2,若AB与⊙C相切,则⊙C的半径是(
)
A
B
C
D
5、如图,在△ABC中,∠C=90°,AC=8,
AB=10,点P在AC上,AP=2,若⊙O的圆
心在线段BP上,且⊙O与AB、AC都相
切,则⊙O的半径为(
)
A
1
B
C
D
6、⊙O内最长弦的长为,直线与⊙O相离,设点O到的距离为,则与的关系是
。
7、如图,P(4,3)是平面直角坐标系内一点,
以P点为圆心,R为半径的圆与
坐标轴
有三个交点,则R的取值是
。
8、在Rt△ABC中∠C=
90°,AC=3cm,BC=4cm,
以C为圆心,
r为半径的圆与AB有怎样的关系?
为什么?
(1)
r
=2cm
(2)
r
=2.4cm
(3)
r
=3cm
9、圆心到直线的距离为,⊙O的半径为,若、是方程的两个实数根,则直线与⊙O的位置关系是怎样的?
10、在Rt△ABC中,AC=3,BC=4,∠ACB=90?.若以点C为圆心,r为半径的圆与直线AB不相离,求r的取值范围。
11、如图,在Rt△ABC中,∠ACB=90?.
(1)先作∠ABC的平分线交AC边于点O,再以点O为圆心,OC为半径作⊙O(要求:尺规作图,保留作图痕迹,不写作法);
(2)请你判断(1)中AB与⊙O的位置关系,并证明你的结论。
12、在平面直角坐标系中,⊙O′与x轴相交于A(2,0),B(8,0),⊙O′的圆心O′在直线y=45x上,求⊙O′的半径,并判断⊙O′与y轴的位置关系.
13、如图,Rt△ABC中,∠ACB=90?,AC=4,BA=5.P是AC上的动点(P不与A.?C重合),设PC=x,点P到AB的距离为y.
(1)求y与x的函数关系式;
(2)试讨论以P为圆心,半径长为x的圆与AB所在直线的位置关系,并指出相应的x的取值范围。
执笔:郭玉闯
审核:余亚丽
学习目标:1、理解圆与直线的位置关系
2、根据直线与圆的公共点的个数或圆心到直线的距离与圆的半径之间的数量关系判断直线与圆的位置关系
3、了解切线的概念,探索切线与过切点的半径之间关系,掌握切线的识别方法
学习重点:直线与圆的三种位置关系及圆的切线的判定。
学习难点:直线与圆的三种位置关系及圆的切线的性质与判定。
学习过程:
一、知识回顾:1、
叫两点间的距离
2、
叫点到直线的距离
二、探索新知:
知识点一:
1、阅读课本P48-50完成下面表格:
直线与圆的位置关系
相交
相切
相离
公共点个数
公共点名称
?
直线名称
?
图
形
?
?
?
圆心到直线距离d与半径r的关系
?
?
?
:判定直线与圆的位置关系的方法有____种
(1)根据定义,由________________的个数来判断
(2)根据性质,由_____________________的关系来判断
练一练:
1、已知⊙O的直径为12cm.
(1)若圆心O到直线l的距离为12cm,则直线l与⊙O
的位置关系为________;
(2)若圆心O到直线l的距离为6cm,则直线l与⊙O
的位置关系为________;
(3)若圆心O到直线l的距离为3cm,则直线l与⊙O
的位置关系为________.
2、已知⊙O的直径为10cm.
(1)若直线l与⊙O相交,则圆心O到直线l的距离为________;
(2)若直线l与⊙O相切,则圆心O到直线l的距离为________;
(3)若直线l与⊙O相离,则圆心O到直线l的距离为________
1、已知圆的直径为10,直线与圆心的距离为4,那么圆和直线有
个公共点。
2、⊙O的半径为,圆心O到直线的距离为,如果=4,=4,那么直线与⊙O的位置关系是
,如果5=3,那么直线与⊙O的位置关系是
。
3、△ABC中,∠C=90°,AC=3,AB=5,以C为圆心,为半径作⊙C,则直线AB与⊙C相离时,的取值范围是
;相切时,的取值范围是取值范围是
;相交时的取值范围是
。⊙C与线段AB相交时,r的取值范围是
。
4、Rt△ABC的斜边AB=4,直角边AC=2,若AB与⊙C相切,则⊙C的半径是(
)
A
B
C
D
5、如图,在△ABC中,∠C=90°,AC=8,
AB=10,点P在AC上,AP=2,若⊙O的圆
心在线段BP上,且⊙O与AB、AC都相
切,则⊙O的半径为(
)
A
1
B
C
D
6、⊙O内最长弦的长为,直线与⊙O相离,设点O到的距离为,则与的关系是
。
7、如图,P(4,3)是平面直角坐标系内一点,
以P点为圆心,R为半径的圆与
坐标轴
有三个交点,则R的取值是
。
8、在Rt△ABC中∠C=
90°,AC=3cm,BC=4cm,
以C为圆心,
r为半径的圆与AB有怎样的关系?
为什么?
(1)
r
=2cm
(2)
r
=2.4cm
(3)
r
=3cm
9、圆心到直线的距离为,⊙O的半径为,若、是方程的两个实数根,则直线与⊙O的位置关系是怎样的?
10、在Rt△ABC中,AC=3,BC=4,∠ACB=90?.若以点C为圆心,r为半径的圆与直线AB不相离,求r的取值范围。
11、如图,在Rt△ABC中,∠ACB=90?.
(1)先作∠ABC的平分线交AC边于点O,再以点O为圆心,OC为半径作⊙O(要求:尺规作图,保留作图痕迹,不写作法);
(2)请你判断(1)中AB与⊙O的位置关系,并证明你的结论。
12、在平面直角坐标系中,⊙O′与x轴相交于A(2,0),B(8,0),⊙O′的圆心O′在直线y=45x上,求⊙O′的半径,并判断⊙O′与y轴的位置关系.
13、如图,Rt△ABC中,∠ACB=90?,AC=4,BA=5.P是AC上的动点(P不与A.?C重合),设PC=x,点P到AB的距离为y.
(1)求y与x的函数关系式;
(2)试讨论以P为圆心,半径长为x的圆与AB所在直线的位置关系,并指出相应的x的取值范围。
