2020-2021学年人教新版七年级数学上册《4.3.3 余角和补角》 高频易错题集 (附解析)
文档属性
| 名称 | 2020-2021学年人教新版七年级数学上册《4.3.3 余角和补角》 高频易错题集 (附解析) |  | |
| 格式 | zip | ||
| 文件大小 | 366.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-17 09:19:37 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
4.3.3
余角和补角
高频易错题集
一.选择题(共10小题)
1.如果一个角的度数比它补角的2倍多30°,那么这个角的度数是( )
A.50°
B.70°
C.130°
D.160°
2.下列语句:①两点确定一条直线,
②两点之间,线段最短,
③等角的余角相等,
④等角的补角相等;
正确的个数是( )
A.1
B.2
C.3
D.4
3.如果∠1与∠2互补,∠2与∠3互余,则∠1与∠3的关系是( )
A.∠1=∠3
B.∠1=180°﹣∠3
C.∠1=90°+∠3
D.∠3=90°+∠1
4.将一副三角板按如图所示位置摆放,其中∠α=∠β的是( )
A.①②
B.②③
C.①④
D.②④
5.在图中,∠ACE的补角、余角分别是( )
A.∠ECB、∠ECD
B.∠ECD、∠ECB
C.∠ACB、∠ACD
D.∠ACB、∠ACD
6.下列说法:①0是绝对值最小的有理数;②一个数的绝对值越大,表示它的点在数轴上离原点越远;③等角的补角相等;④两点之间线段最短.其中正确的个数是( )
A.1个
B.2个
C.3个
D.4个
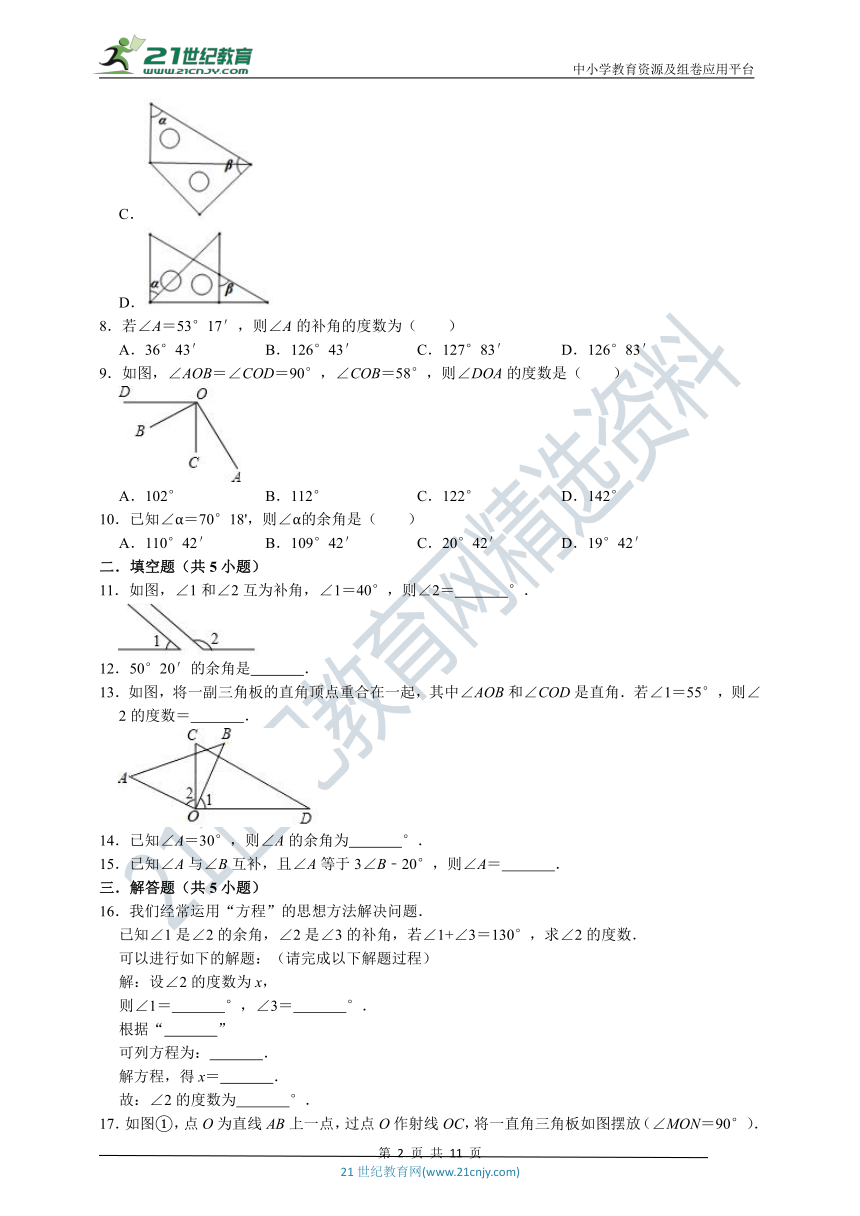
7.一副直角三角板有不同的摆放方式,图中满足∠α与∠β相等的摆放方式是( )
A.
B.
C.
D.
8.若∠A=53°17′,则∠A的补角的度数为( )
A.36°43′
B.126°43′
C.127°83′
D.126°83′
9.如图,∠AOB=∠COD=90°,∠COB=58°,则∠DOA的度数是( )
A.102°
B.112°
C.122°
D.142°
10.已知∠α=70°18',则∠α的余角是( )
A.110°42′
B.109°42′
C.20°42′
D.19°42′
二.填空题(共5小题)
11.如图,∠1和∠2互为补角,∠1=40°,则∠2=
°.
12.50°20′的余角是
.
13.如图,将一副三角板的直角顶点重合在一起,其中∠AOB和∠COD是直角.若∠1=55°,则∠2的度数=
.
14.已知∠A=30°,则∠A的余角为
°.
15.已知∠A与∠B互补,且∠A等于3∠B﹣20°,则∠A=
.
三.解答题(共5小题)
16.我们经常运用“方程”的思想方法解决问题.
已知∠1是∠2的余角,∠2是∠3的补角,若∠1+∠3=130°,求∠2的度数.
可以进行如下的解题:(请完成以下解题过程)
解:设∠2的度数为x,
则∠1=
°,∠3=
°.
根据“
”
可列方程为:
.
解方程,得x=
.
故:∠2的度数为
°.
17.如图①,点O为直线AB上一点,过点O作射线OC,将一直角三角板如图摆放(∠MON=90°).
(1)将图①中的三角板绕点O旋转一定的角度得图②,使边OM恰好平分∠BOC,问:ON是否平分∠AOC?请说明理由;
(2)将图①中的三角板绕点O旋转一定的角度得图③,使边ON在∠BOC的内部,如果∠BOC=60°,则∠BOM与∠NOC之间存在怎样的数量关系?请说明理由.
18.如图1,点O为直线AB上一点,过点O作射线OC,使∠BOC=2∠AOC,将一直角三角板的直角顶点放在点O处,边OM在射线OB上,另一边ON在直线AB的下方.
(1)将图1中的三角板绕点O按逆时针方向旋转45°至图2的位置,此时∠MOC=
°;
(2)将图1中的三角板绕点O按逆时针方向旋转至图3的位置,使得ON在∠AOC的内部.试探究∠AOM与∠NOC之间满足什么等量关系,并说明理由;
(3)在上述直角三角板从图1逆时针旋转一周的过程中,若三角板绕点O按5°每秒的速度旋转,当直角三角板的直角边ON所在直线恰好平分∠AOC时,求此时三角板绕点O的运动时间t的值.
19.如图,已知AOB是一条直线,∠1=∠2,∠3=∠4,∠AOF=∠BOF=90°.则
(1)∠AOC的补角是
;
(2)∠AOC的余角是
;
(3)∠COF的补角是
;
(4)∠EOF的余角是
.
20.如图,∠AOC和∠DOB都是直角.
(1)如图1,如果∠DOC=32°,求∠AOB的度数;
(2)找出图1中相等的锐角,并说明相等的理由;
(3)在图2中,利用三角板画一个与∠FOE相等的角.
试题解析
一.选择题(共10小题)
1.如果一个角的度数比它补角的2倍多30°,那么这个角的度数是( )
A.50°
B.70°
C.130°
D.160°
解:设这个角是x°,根据题意,得
x=2(180﹣x)+30,
解得:x=130.
即这个角的度数为130°.
故选:C.
2.下列语句:①两点确定一条直线,
②两点之间,线段最短,
③等角的余角相等,
④等角的补角相等;
正确的个数是( )
A.1
B.2
C.3
D.4
解:①两点确定一条直线,正确;
②两点之间,线段最短,正确;
③等角的余角相等,正确;
④等角的补角相等,正确.
所以正确的说法有①②③④共4个.
故选:D.
3.如果∠1与∠2互补,∠2与∠3互余,则∠1与∠3的关系是( )
A.∠1=∠3
B.∠1=180°﹣∠3
C.∠1=90°+∠3
D.∠3=90°+∠1
解:∵∠1+∠2=180°
∴∠1=180°﹣∠2
又∵∠2+∠3=90°
∴∠3=90°﹣∠2
∴∠1﹣∠3=90°,即∠1=90°+∠3.
故选:C.
4.将一副三角板按如图所示位置摆放,其中∠α=∠β的是( )
A.①②
B.②③
C.①④
D.②④
解:A图形中,根据同角的余角相等可得∠α=∠β;
B图形中,∠α>∠β
C图形中,∠α<∠β
D图形中,∠α=∠β=45°.
所以∠α=∠β的是①④.
故选:C.
5.在图中,∠ACE的补角、余角分别是( )
A.∠ECB、∠ECD
B.∠ECD、∠ECB
C.∠ACB、∠ACD
D.∠ACB、∠ACD
解:∠ACE的补角是∠ECB,∠ACE的余角是∠ECD.
故选:A.
6.下列说法:①0是绝对值最小的有理数;②一个数的绝对值越大,表示它的点在数轴上离原点越远;③等角的补角相等;④两点之间线段最短.其中正确的个数是( )
A.1个
B.2个
C.3个
D.4个
解:根据绝对值的定义是数轴上点到原点的距离,可知①②正确;
根据补角的性质可知等角的补角相等,故③正确;
根据线段的性质可知两点之间线段最短,故④正确;
正确的个数是4个,
故选:D.
7.一副直角三角板有不同的摆放方式,图中满足∠α与∠β相等的摆放方式是( )
A.
B.
C.
D.
解:选项B中,∠α、∠β都与中间的锐角互余,根据同角的余角相等可得∠α=∠β,
故选:B.
8.若∠A=53°17′,则∠A的补角的度数为( )
A.36°43′
B.126°43′
C.127°83′
D.126°83′
解:∵∠A=53°17′,
∴∠A的补角=180°﹣53°17′=126°43′.
故选:B.
9.如图,∠AOB=∠COD=90°,∠COB=58°,则∠DOA的度数是( )
A.102°
B.112°
C.122°
D.142°
解:∵∠AOB=∠COD=90°,∠COB=58°,
∴∠BOD=∠COA=90°﹣58°=32°,
∴∠DOA=∠AOB+∠DOB=90°+32°=122°.
故选:C.
10.已知∠α=70°18',则∠α的余角是( )
A.110°42′
B.109°42′
C.20°42′
D.19°42′
解:∠A的余角为90°﹣70°18'=19°42′,
故选:D.
二.填空题(共5小题)
11.如图,∠1和∠2互为补角,∠1=40°,则∠2= 140 °.
解:∵∠1和∠2互为补角,
∴∠1+∠2=180°,
∵∠1=40°,
∴∠2=180°﹣∠1=180°﹣40°=140°,
故答案为:140.
12.50°20′的余角是 39°40' .
解:50°20′的余角是90°﹣50°20′=39°40′.
故答案是:39°40′.
13.如图,将一副三角板的直角顶点重合在一起,其中∠AOB和∠COD是直角.若∠1=55°,则∠2的度数= 55° .
解:∵∠AOB和∠COD是直角,
∴∠BOC+∠1=90°=∠BOC+∠2,
∴∠1=∠2=55°,
故答案为:55°.
14.已知∠A=30°,则∠A的余角为 60 °.
解:∵∠A=30°,
∴∠A的余角=90°﹣30°=60°.
故答案为:60.
15.已知∠A与∠B互补,且∠A等于3∠B﹣20°,则∠A= 130° .
解:∵∠A与∠B互补,
∴∠A+∠B=180°,
∵∠A=3∠B﹣20°,
∴3∠B﹣20°+∠B=180°,
∴4∠B=180°+20°,
∴∠B=50°,
∠A=180°﹣50°=130°.
故答案为:130°.
三.解答题(共5小题)
16.我们经常运用“方程”的思想方法解决问题.
已知∠1是∠2的余角,∠2是∠3的补角,若∠1+∠3=130°,求∠2的度数.
可以进行如下的解题:(请完成以下解题过程)
解:设∠2的度数为x,
则∠1= (90﹣x) °,∠3= (180﹣x) °.
根据“ ∠1+∠3=130° ”
可列方程为: (90﹣x)+(180﹣x)=130 .
解方程,得x= 70 .
故:∠2的度数为 70 °.
解:设∠2的度数为x,
则∠1=(90﹣x)°,∠3=(180﹣x)°.
根据“∠1+∠3=130°”
可列方程为:(90﹣x)+(180﹣x)=130.
解方程,得x=70.
故:∠2的度数为70°.
故答案为:(90﹣x);(180﹣x);∠1+∠3=130°;(90﹣x)+(180﹣x)=130;70;70.
17.如图①,点O为直线AB上一点,过点O作射线OC,将一直角三角板如图摆放(∠MON=90°).
(1)将图①中的三角板绕点O旋转一定的角度得图②,使边OM恰好平分∠BOC,问:ON是否平分∠AOC?请说明理由;
(2)将图①中的三角板绕点O旋转一定的角度得图③,使边ON在∠BOC的内部,如果∠BOC=60°,则∠BOM与∠NOC之间存在怎样的数量关系?请说明理由.
解:(1)ON平分∠AOC.
理由如下:∵∠MON=90°,
∴∠BOM+∠AON=90°,∠MOC+∠NOC=90°.
又∵OM平分∠BOC,
∴∠BOM=∠MOC,
∴∠AON=∠NOC.
∴ON平分∠AOC.
(2)∠BOM=∠NOC+30°.
理由如下:∵∠CON+∠NOB=60°,∠BOM+∠NOB=90°,
∴∠BOM=90°﹣∠NOB=90°﹣(60°﹣∠NOC)=∠NOC+30°.
∴∠BOM与∠NOC之间存在的数量关系是:∠BOM=∠NOC+30°.
18.如图1,点O为直线AB上一点,过点O作射线OC,使∠BOC=2∠AOC,将一直角三角板的直角顶点放在点O处,边OM在射线OB上,另一边ON在直线AB的下方.
(1)将图1中的三角板绕点O按逆时针方向旋转45°至图2的位置,此时∠MOC= 75 °;
(2)将图1中的三角板绕点O按逆时针方向旋转至图3的位置,使得ON在∠AOC的内部.试探究∠AOM与∠NOC之间满足什么等量关系,并说明理由;
(3)在上述直角三角板从图1逆时针旋转一周的过程中,若三角板绕点O按5°每秒的速度旋转,当直角三角板的直角边ON所在直线恰好平分∠AOC时,求此时三角板绕点O的运动时间t的值.
解:(1)∵∠BOC+∠AOC=180°,∠BOC=2∠AOC,
∴∠AOC=60°,∠BOC=120°,
由旋转可知∠BOM=45°,
∵OM恰好平分∠BOC,
∴∠MOC=120°﹣45°=75°.
故答案为:75.
(2)由(1)得∠AOC=60°,
∵∠MON=90°,
∴∠AOM=90°﹣∠AON,∠NOC=60°﹣∠AON,
∴∠AOM﹣∠NOC=(90°﹣∠AON)﹣(60°﹣∠AON)=30°,
∴∠AOM与∠NOC之间的数量关系为:∠AOM﹣∠NOC=30°.
(3)由(1)得∠AOC=60°,
①如左图,延长NO,
当直线ON恰好平分锐角∠AOC,
∴∠AOD=∠COD=30°,
即逆时针旋转60°时NO延长线平分∠AOC,
由题意得,5t=60,
∴t=12;
如右图,当NO平分∠AOC,
∴∠AON=30°,
即逆时针旋转240°时NO平分∠AOC,
∴5t=240,
∴t=48,
∴三角板绕点O的运动时间为12秒或48秒.
19.如图,已知AOB是一条直线,∠1=∠2,∠3=∠4,∠AOF=∠BOF=90°.则
(1)∠AOC的补角是 ∠COB ;
(2)∠AOC的余角是 ∠3、∠4 ;
(3)∠COF的补角是 ∠AOE ;
(4)∠EOF的余角是 ∠3、∠4 .
解:根据题意和图示可知:
(1)∠AOC+∠BOC=180°,
故答案为:∠COB;
(2)∠3=∠4,∠AOC+∠3=90°,
故答案为:∠3、∠4;
(3)∵∠3=∠4,
∴∠COF的补角是∠AOE,
故答案为:∠AOE;
(4)∵∠EOF+∠4=90°,
∴∠4是∠EOF的余角,
∵∠3=∠4,
∴∠3也是∠EOF的余角,
∴∠EOF的余角是∠3、∠4,
故答案为:∠3、∠4.
20.如图,∠AOC和∠DOB都是直角.
(1)如图1,如果∠DOC=32°,求∠AOB的度数;
(2)找出图1中相等的锐角,并说明相等的理由;
(3)在图2中,利用三角板画一个与∠FOE相等的角.
解:(1)∵∠DOC=32°,∠AOC=90°,
∴∠AOD=58°,
又∵∠BOD=90°,
∴∠AOB=∠AOD+∠BOD=58°+90°=148°;
(2)∠AOD=∠BOC;
理由:∵∠AOD=∠BOD,
∴∠AOD+∠COD=∠BOC+∠COD,
∴∠AOD=∠BOC;
(3)如图所示,∠GOH=∠EOF.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
4.3.3
余角和补角
高频易错题集
一.选择题(共10小题)
1.如果一个角的度数比它补角的2倍多30°,那么这个角的度数是( )
A.50°
B.70°
C.130°
D.160°
2.下列语句:①两点确定一条直线,
②两点之间,线段最短,
③等角的余角相等,
④等角的补角相等;
正确的个数是( )
A.1
B.2
C.3
D.4
3.如果∠1与∠2互补,∠2与∠3互余,则∠1与∠3的关系是( )
A.∠1=∠3
B.∠1=180°﹣∠3
C.∠1=90°+∠3
D.∠3=90°+∠1
4.将一副三角板按如图所示位置摆放,其中∠α=∠β的是( )
A.①②
B.②③
C.①④
D.②④
5.在图中,∠ACE的补角、余角分别是( )
A.∠ECB、∠ECD
B.∠ECD、∠ECB
C.∠ACB、∠ACD
D.∠ACB、∠ACD
6.下列说法:①0是绝对值最小的有理数;②一个数的绝对值越大,表示它的点在数轴上离原点越远;③等角的补角相等;④两点之间线段最短.其中正确的个数是( )
A.1个
B.2个
C.3个
D.4个
7.一副直角三角板有不同的摆放方式,图中满足∠α与∠β相等的摆放方式是( )
A.
B.
C.
D.
8.若∠A=53°17′,则∠A的补角的度数为( )
A.36°43′
B.126°43′
C.127°83′
D.126°83′
9.如图,∠AOB=∠COD=90°,∠COB=58°,则∠DOA的度数是( )
A.102°
B.112°
C.122°
D.142°
10.已知∠α=70°18',则∠α的余角是( )
A.110°42′
B.109°42′
C.20°42′
D.19°42′
二.填空题(共5小题)
11.如图,∠1和∠2互为补角,∠1=40°,则∠2=
°.
12.50°20′的余角是
.
13.如图,将一副三角板的直角顶点重合在一起,其中∠AOB和∠COD是直角.若∠1=55°,则∠2的度数=
.
14.已知∠A=30°,则∠A的余角为
°.
15.已知∠A与∠B互补,且∠A等于3∠B﹣20°,则∠A=
.
三.解答题(共5小题)
16.我们经常运用“方程”的思想方法解决问题.
已知∠1是∠2的余角,∠2是∠3的补角,若∠1+∠3=130°,求∠2的度数.
可以进行如下的解题:(请完成以下解题过程)
解:设∠2的度数为x,
则∠1=
°,∠3=
°.
根据“
”
可列方程为:
.
解方程,得x=
.
故:∠2的度数为
°.
17.如图①,点O为直线AB上一点,过点O作射线OC,将一直角三角板如图摆放(∠MON=90°).
(1)将图①中的三角板绕点O旋转一定的角度得图②,使边OM恰好平分∠BOC,问:ON是否平分∠AOC?请说明理由;
(2)将图①中的三角板绕点O旋转一定的角度得图③,使边ON在∠BOC的内部,如果∠BOC=60°,则∠BOM与∠NOC之间存在怎样的数量关系?请说明理由.
18.如图1,点O为直线AB上一点,过点O作射线OC,使∠BOC=2∠AOC,将一直角三角板的直角顶点放在点O处,边OM在射线OB上,另一边ON在直线AB的下方.
(1)将图1中的三角板绕点O按逆时针方向旋转45°至图2的位置,此时∠MOC=
°;
(2)将图1中的三角板绕点O按逆时针方向旋转至图3的位置,使得ON在∠AOC的内部.试探究∠AOM与∠NOC之间满足什么等量关系,并说明理由;
(3)在上述直角三角板从图1逆时针旋转一周的过程中,若三角板绕点O按5°每秒的速度旋转,当直角三角板的直角边ON所在直线恰好平分∠AOC时,求此时三角板绕点O的运动时间t的值.
19.如图,已知AOB是一条直线,∠1=∠2,∠3=∠4,∠AOF=∠BOF=90°.则
(1)∠AOC的补角是
;
(2)∠AOC的余角是
;
(3)∠COF的补角是
;
(4)∠EOF的余角是
.
20.如图,∠AOC和∠DOB都是直角.
(1)如图1,如果∠DOC=32°,求∠AOB的度数;
(2)找出图1中相等的锐角,并说明相等的理由;
(3)在图2中,利用三角板画一个与∠FOE相等的角.
试题解析
一.选择题(共10小题)
1.如果一个角的度数比它补角的2倍多30°,那么这个角的度数是( )
A.50°
B.70°
C.130°
D.160°
解:设这个角是x°,根据题意,得
x=2(180﹣x)+30,
解得:x=130.
即这个角的度数为130°.
故选:C.
2.下列语句:①两点确定一条直线,
②两点之间,线段最短,
③等角的余角相等,
④等角的补角相等;
正确的个数是( )
A.1
B.2
C.3
D.4
解:①两点确定一条直线,正确;
②两点之间,线段最短,正确;
③等角的余角相等,正确;
④等角的补角相等,正确.
所以正确的说法有①②③④共4个.
故选:D.
3.如果∠1与∠2互补,∠2与∠3互余,则∠1与∠3的关系是( )
A.∠1=∠3
B.∠1=180°﹣∠3
C.∠1=90°+∠3
D.∠3=90°+∠1
解:∵∠1+∠2=180°
∴∠1=180°﹣∠2
又∵∠2+∠3=90°
∴∠3=90°﹣∠2
∴∠1﹣∠3=90°,即∠1=90°+∠3.
故选:C.
4.将一副三角板按如图所示位置摆放,其中∠α=∠β的是( )
A.①②
B.②③
C.①④
D.②④
解:A图形中,根据同角的余角相等可得∠α=∠β;
B图形中,∠α>∠β
C图形中,∠α<∠β
D图形中,∠α=∠β=45°.
所以∠α=∠β的是①④.
故选:C.
5.在图中,∠ACE的补角、余角分别是( )
A.∠ECB、∠ECD
B.∠ECD、∠ECB
C.∠ACB、∠ACD
D.∠ACB、∠ACD
解:∠ACE的补角是∠ECB,∠ACE的余角是∠ECD.
故选:A.
6.下列说法:①0是绝对值最小的有理数;②一个数的绝对值越大,表示它的点在数轴上离原点越远;③等角的补角相等;④两点之间线段最短.其中正确的个数是( )
A.1个
B.2个
C.3个
D.4个
解:根据绝对值的定义是数轴上点到原点的距离,可知①②正确;
根据补角的性质可知等角的补角相等,故③正确;
根据线段的性质可知两点之间线段最短,故④正确;
正确的个数是4个,
故选:D.
7.一副直角三角板有不同的摆放方式,图中满足∠α与∠β相等的摆放方式是( )
A.
B.
C.
D.
解:选项B中,∠α、∠β都与中间的锐角互余,根据同角的余角相等可得∠α=∠β,
故选:B.
8.若∠A=53°17′,则∠A的补角的度数为( )
A.36°43′
B.126°43′
C.127°83′
D.126°83′
解:∵∠A=53°17′,
∴∠A的补角=180°﹣53°17′=126°43′.
故选:B.
9.如图,∠AOB=∠COD=90°,∠COB=58°,则∠DOA的度数是( )
A.102°
B.112°
C.122°
D.142°
解:∵∠AOB=∠COD=90°,∠COB=58°,
∴∠BOD=∠COA=90°﹣58°=32°,
∴∠DOA=∠AOB+∠DOB=90°+32°=122°.
故选:C.
10.已知∠α=70°18',则∠α的余角是( )
A.110°42′
B.109°42′
C.20°42′
D.19°42′
解:∠A的余角为90°﹣70°18'=19°42′,
故选:D.
二.填空题(共5小题)
11.如图,∠1和∠2互为补角,∠1=40°,则∠2= 140 °.
解:∵∠1和∠2互为补角,
∴∠1+∠2=180°,
∵∠1=40°,
∴∠2=180°﹣∠1=180°﹣40°=140°,
故答案为:140.
12.50°20′的余角是 39°40' .
解:50°20′的余角是90°﹣50°20′=39°40′.
故答案是:39°40′.
13.如图,将一副三角板的直角顶点重合在一起,其中∠AOB和∠COD是直角.若∠1=55°,则∠2的度数= 55° .
解:∵∠AOB和∠COD是直角,
∴∠BOC+∠1=90°=∠BOC+∠2,
∴∠1=∠2=55°,
故答案为:55°.
14.已知∠A=30°,则∠A的余角为 60 °.
解:∵∠A=30°,
∴∠A的余角=90°﹣30°=60°.
故答案为:60.
15.已知∠A与∠B互补,且∠A等于3∠B﹣20°,则∠A= 130° .
解:∵∠A与∠B互补,
∴∠A+∠B=180°,
∵∠A=3∠B﹣20°,
∴3∠B﹣20°+∠B=180°,
∴4∠B=180°+20°,
∴∠B=50°,
∠A=180°﹣50°=130°.
故答案为:130°.
三.解答题(共5小题)
16.我们经常运用“方程”的思想方法解决问题.
已知∠1是∠2的余角,∠2是∠3的补角,若∠1+∠3=130°,求∠2的度数.
可以进行如下的解题:(请完成以下解题过程)
解:设∠2的度数为x,
则∠1= (90﹣x) °,∠3= (180﹣x) °.
根据“ ∠1+∠3=130° ”
可列方程为: (90﹣x)+(180﹣x)=130 .
解方程,得x= 70 .
故:∠2的度数为 70 °.
解:设∠2的度数为x,
则∠1=(90﹣x)°,∠3=(180﹣x)°.
根据“∠1+∠3=130°”
可列方程为:(90﹣x)+(180﹣x)=130.
解方程,得x=70.
故:∠2的度数为70°.
故答案为:(90﹣x);(180﹣x);∠1+∠3=130°;(90﹣x)+(180﹣x)=130;70;70.
17.如图①,点O为直线AB上一点,过点O作射线OC,将一直角三角板如图摆放(∠MON=90°).
(1)将图①中的三角板绕点O旋转一定的角度得图②,使边OM恰好平分∠BOC,问:ON是否平分∠AOC?请说明理由;
(2)将图①中的三角板绕点O旋转一定的角度得图③,使边ON在∠BOC的内部,如果∠BOC=60°,则∠BOM与∠NOC之间存在怎样的数量关系?请说明理由.
解:(1)ON平分∠AOC.
理由如下:∵∠MON=90°,
∴∠BOM+∠AON=90°,∠MOC+∠NOC=90°.
又∵OM平分∠BOC,
∴∠BOM=∠MOC,
∴∠AON=∠NOC.
∴ON平分∠AOC.
(2)∠BOM=∠NOC+30°.
理由如下:∵∠CON+∠NOB=60°,∠BOM+∠NOB=90°,
∴∠BOM=90°﹣∠NOB=90°﹣(60°﹣∠NOC)=∠NOC+30°.
∴∠BOM与∠NOC之间存在的数量关系是:∠BOM=∠NOC+30°.
18.如图1,点O为直线AB上一点,过点O作射线OC,使∠BOC=2∠AOC,将一直角三角板的直角顶点放在点O处,边OM在射线OB上,另一边ON在直线AB的下方.
(1)将图1中的三角板绕点O按逆时针方向旋转45°至图2的位置,此时∠MOC= 75 °;
(2)将图1中的三角板绕点O按逆时针方向旋转至图3的位置,使得ON在∠AOC的内部.试探究∠AOM与∠NOC之间满足什么等量关系,并说明理由;
(3)在上述直角三角板从图1逆时针旋转一周的过程中,若三角板绕点O按5°每秒的速度旋转,当直角三角板的直角边ON所在直线恰好平分∠AOC时,求此时三角板绕点O的运动时间t的值.
解:(1)∵∠BOC+∠AOC=180°,∠BOC=2∠AOC,
∴∠AOC=60°,∠BOC=120°,
由旋转可知∠BOM=45°,
∵OM恰好平分∠BOC,
∴∠MOC=120°﹣45°=75°.
故答案为:75.
(2)由(1)得∠AOC=60°,
∵∠MON=90°,
∴∠AOM=90°﹣∠AON,∠NOC=60°﹣∠AON,
∴∠AOM﹣∠NOC=(90°﹣∠AON)﹣(60°﹣∠AON)=30°,
∴∠AOM与∠NOC之间的数量关系为:∠AOM﹣∠NOC=30°.
(3)由(1)得∠AOC=60°,
①如左图,延长NO,
当直线ON恰好平分锐角∠AOC,
∴∠AOD=∠COD=30°,
即逆时针旋转60°时NO延长线平分∠AOC,
由题意得,5t=60,
∴t=12;
如右图,当NO平分∠AOC,
∴∠AON=30°,
即逆时针旋转240°时NO平分∠AOC,
∴5t=240,
∴t=48,
∴三角板绕点O的运动时间为12秒或48秒.
19.如图,已知AOB是一条直线,∠1=∠2,∠3=∠4,∠AOF=∠BOF=90°.则
(1)∠AOC的补角是 ∠COB ;
(2)∠AOC的余角是 ∠3、∠4 ;
(3)∠COF的补角是 ∠AOE ;
(4)∠EOF的余角是 ∠3、∠4 .
解:根据题意和图示可知:
(1)∠AOC+∠BOC=180°,
故答案为:∠COB;
(2)∠3=∠4,∠AOC+∠3=90°,
故答案为:∠3、∠4;
(3)∵∠3=∠4,
∴∠COF的补角是∠AOE,
故答案为:∠AOE;
(4)∵∠EOF+∠4=90°,
∴∠4是∠EOF的余角,
∵∠3=∠4,
∴∠3也是∠EOF的余角,
∴∠EOF的余角是∠3、∠4,
故答案为:∠3、∠4.
20.如图,∠AOC和∠DOB都是直角.
(1)如图1,如果∠DOC=32°,求∠AOB的度数;
(2)找出图1中相等的锐角,并说明相等的理由;
(3)在图2中,利用三角板画一个与∠FOE相等的角.
解:(1)∵∠DOC=32°,∠AOC=90°,
∴∠AOD=58°,
又∵∠BOD=90°,
∴∠AOB=∠AOD+∠BOD=58°+90°=148°;
(2)∠AOD=∠BOC;
理由:∵∠AOD=∠BOD,
∴∠AOD+∠COD=∠BOC+∠COD,
∴∠AOD=∠BOC;
(3)如图所示,∠GOH=∠EOF.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
