2020-2021学年人教新版七年级数学上册《4.4 课题学习 设计制作长方体形状的包装纸盒》 高频易错题集 (附解析)
文档属性
| 名称 | 2020-2021学年人教新版七年级数学上册《4.4 课题学习 设计制作长方体形状的包装纸盒》 高频易错题集 (附解析) |  | |
| 格式 | zip | ||
| 文件大小 | 385.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-17 09:23:40 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
4.4
课题学习
设计制作长方体形状的包装纸盒
高频易错题集
一.选择题(共10小题)
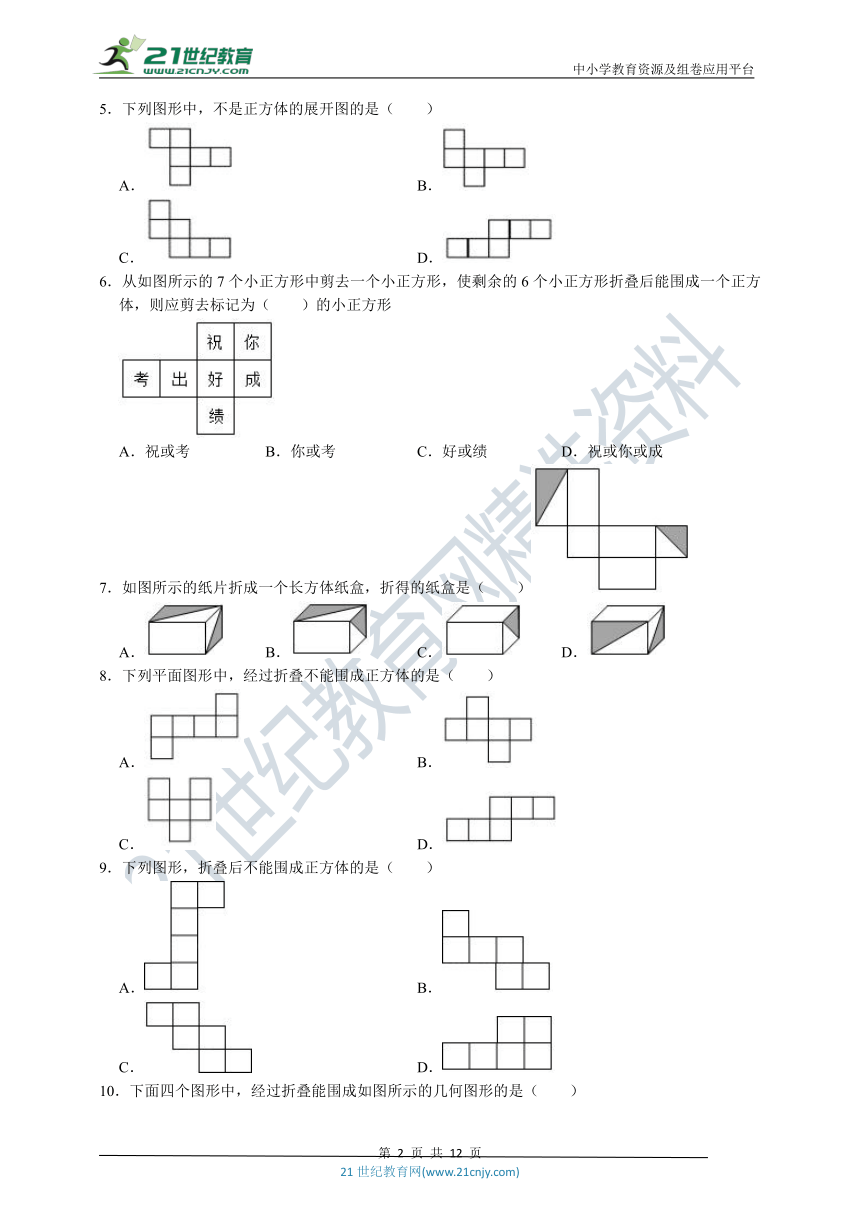
1.如图是某个几何体的展开图,该几何体是( )
A.三棱柱
B.三棱锥
C.圆柱
D.圆锥
2.正方体展开后,不能得到的展开图是( )
A.
B.
C.
D.
3.一个正方体的表面展开图可以是下列图形中的( )
A.
B.
C.
D.
4.如图正方体纸盒,展开后可以得到( )
A.
B.
C.
D.
5.下列图形中,不是正方体的展开图的是( )
A.
B.
C.
D.
6.从如图所示的7个小正方形中剪去一个小正方形,使剩余的6个小正方形折叠后能围成一个正方体,则应剪去标记为( )的小正方形
A.祝或考
B.你或考
C.好或绩
D.祝或你或成
7.如图所示的纸片折成一个长方体纸盒,折得的纸盒是( )
A.
B.
C.
D.
8.下列平面图形中,经过折叠不能围成正方体的是( )
A.
B.
C.
D.
9.下列图形,折叠后不能围成正方体的是( )
A.
B.
C.
D.
10.下面四个图形中,经过折叠能围成如图所示的几何图形的是( )
A.
B.
C.
D.
二.填空题(共5小题)
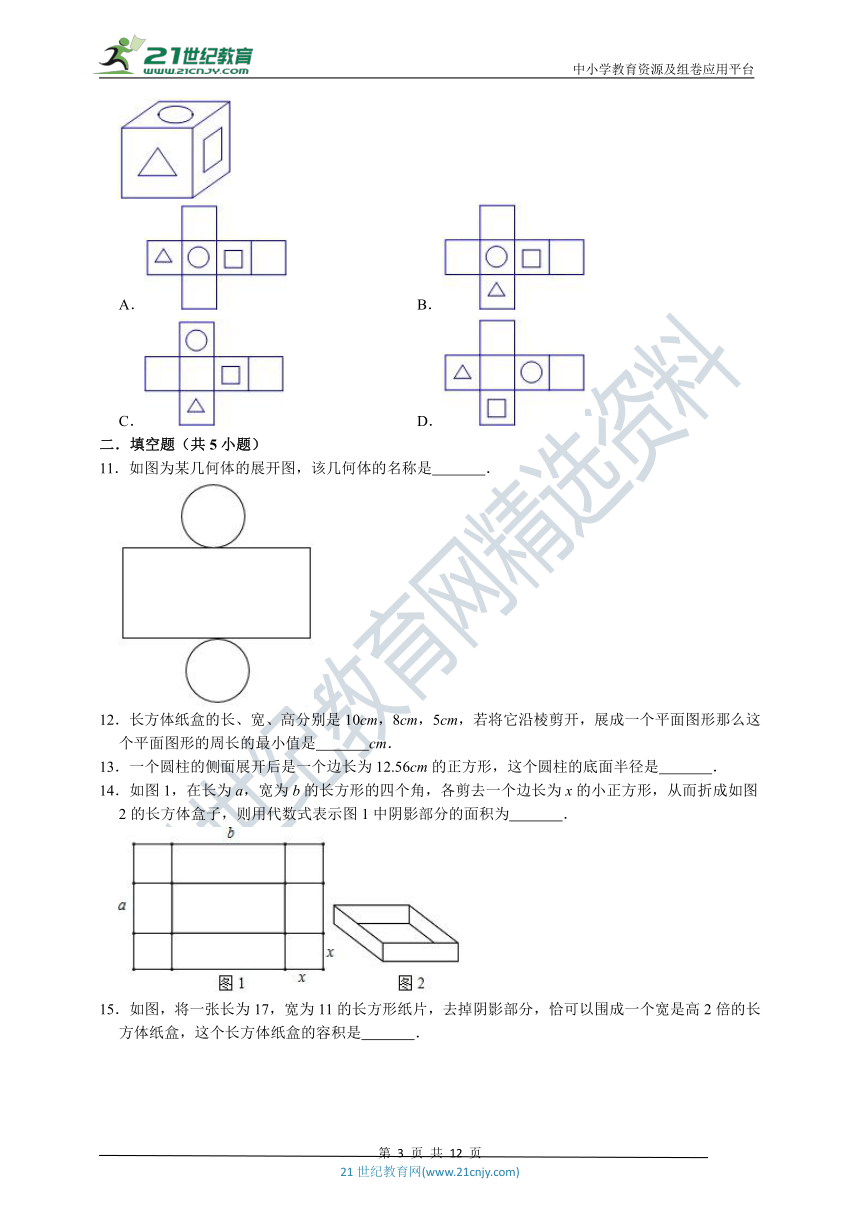
11.如图为某几何体的展开图,该几何体的名称是
.
12.长方体纸盒的长、宽、高分别是10cm,8cm,5cm,若将它沿棱剪开,展成一个平面图形那么这个平面图形的周长的最小值是
cm.
13.一个圆柱的侧面展开后是一个边长为12.56cm的正方形,这个圆柱的底面半径是
.
14.如图1,在长为a,宽为b的长方形的四个角,各剪去一个边长为x的小正方形,从而折成如图2的长方体盒子,则用代数式表示图1中阴影部分的面积为
.
15.如图,将一张长为17,宽为11的长方形纸片,去掉阴影部分,恰可以围成一个宽是高2倍的长方体纸盒,这个长方体纸盒的容积是
.
三.解答题(共5小题)
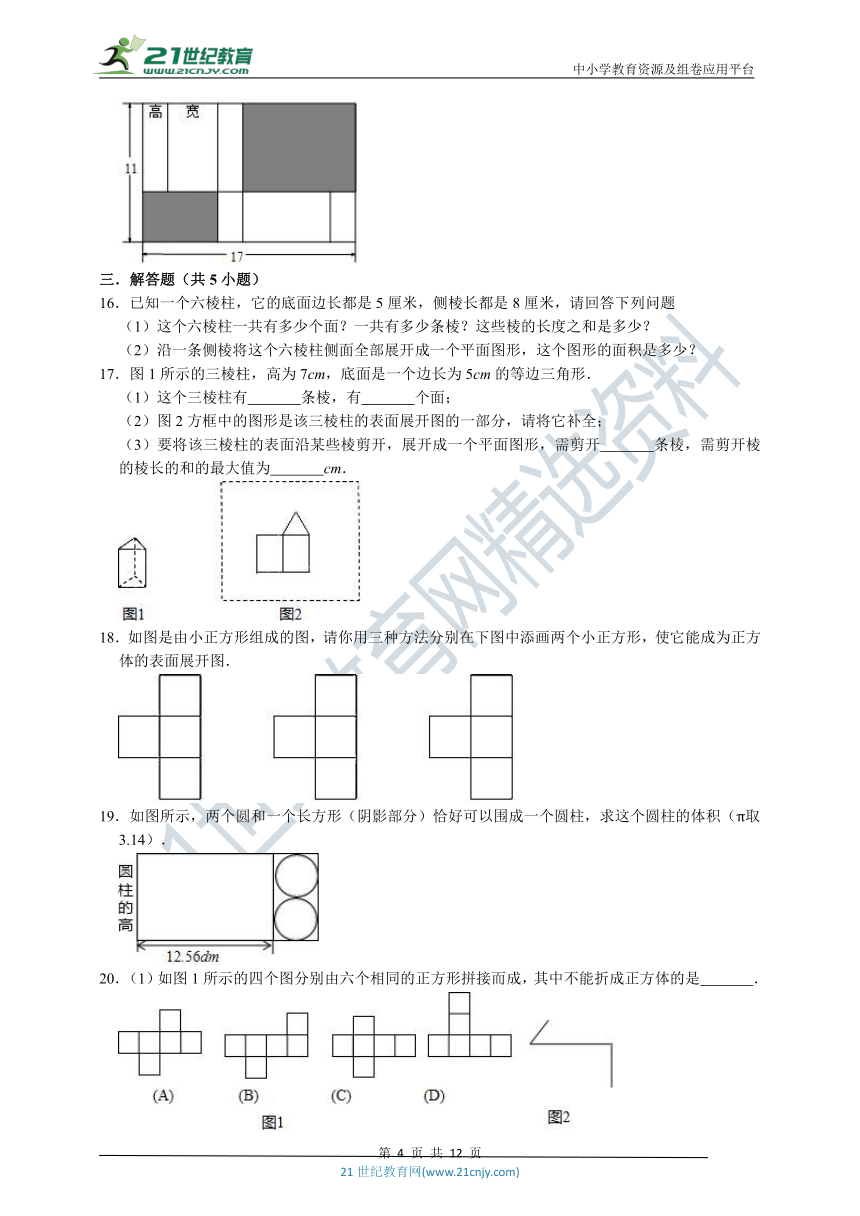
16.已知一个六棱柱,它的底面边长都是5厘米,侧棱长都是8厘米,请回答下列问题
(1)这个六棱柱一共有多少个面?一共有多少条棱?这些棱的长度之和是多少?
(2)沿一条侧棱将这个六棱柱侧面全部展开成一个平面图形,这个图形的面积是多少?
17.图1所示的三棱柱,高为7cm,底面是一个边长为5cm的等边三角形.
(1)这个三棱柱有
条棱,有
个面;
(2)图2方框中的图形是该三棱柱的表面展开图的一部分,请将它补全;
(3)要将该三棱柱的表面沿某些棱剪开,展开成一个平面图形,需剪开
条棱,需剪开棱的棱长的和的最大值为
cm.
18.如图是由小正方形组成的图,请你用三种方法分别在下图中添画两个小正方形,使它能成为正方体的表面展开图.
19.如图所示,两个圆和一个长方形(阴影部分)恰好可以围成一个圆柱,求这个圆柱的体积(π取3.14).
20.(1)如图1所示的四个图分别由六个相同的正方形拼接而成,其中不能折成正方体的是
.
(2)用斜二测画法补画图2,使它成为长方体的直观图.(注:遮住的线段用虚线表示,保留痕迹,不必写画法)
(3)在这一长方体中,从同一个顶点出发的三个面的面积之比为5:7:2,其中最大的面积比最小的面积大30cm2,求这个长方体的表面积.
试题解析
一.选择题(共10小题)
1.如图是某个几何体的展开图,该几何体是( )
A.三棱柱
B.三棱锥
C.圆柱
D.圆锥
解:观察图形可知,这个几何体是三棱柱.
故选:A.
2.正方体展开后,不能得到的展开图是( )
A.
B.
C.
D.
解:选项B、C、D都能折叠成正方体,只有选项A中,出现“田”字形,不能折成正方体.
故选:A.
3.一个正方体的表面展开图可以是下列图形中的( )
A.
B.
C.
D.
解:A,C,D折叠后有一行两个面无法折起来,从而缺少面,不能折成正方体,只有B是一个正方体的表面展开图.
故选:B.
4.如图正方体纸盒,展开后可以得到( )
A.
B.
C.
D.
解:A.两个蓝色圆所在的面折叠后是对面,不合题意;
B.白色圆与一个蓝色圆所在的面折叠后是对面,不合题意;
C.白色圆与一个蓝色圆所在的面折叠后是对面,不合题意;
D.白色圆与两个蓝色圆所在的面折叠后是相邻的面,符合题意;
故选:D.
5.下列图形中,不是正方体的展开图的是( )
A.
B.
C.
D.
解:A、B、D可组成正方体;
C不能组成正方体.
故选:C.
6.从如图所示的7个小正方形中剪去一个小正方形,使剩余的6个小正方形折叠后能围成一个正方体,则应剪去标记为( )的小正方形
A.祝或考
B.你或考
C.好或绩
D.祝或你或成
解:由图可得,与“绩”相对的面不唯一,与“出”相对的面不唯一,
将如图所示的图形剪去一个小正方形,使余下的部分恰好能折成一个正方体,应剪去标记为祝或你或成的小正方形,
故选:D.
7.如图所示的纸片折成一个长方体纸盒,折得的纸盒是( )
A.
B.
C.
D.
解:如图所示:
根据题意可知,A的对面是A′,B的对面是B′,C的对面是C′,A的短边阴影与C的阴影重合.
故用形如图所示的纸片折成一个长方体纸盒,折得的纸盒是C.
故选:C.
8.下列平面图形中,经过折叠不能围成正方体的是( )
A.
B.
C.
D.
解:由展开图可知:A、B、D能围成正方体,故不符合题意;
C、围成几何体时,有两个面重合,不能围成正方体,故符合题意.
故选:C.
9.下列图形,折叠后不能围成正方体的是( )
A.
B.
C.
D.
解:由展开图可知:A、B、C能围成正方体,不符合题意;
D、是“田”字形,围成几何体时,有两个面重合,故不能围成正方体,符合题意.
故选:D.
10.下面四个图形中,经过折叠能围成如图所示的几何图形的是( )
A.
B.
C.
D.
解:根据立体图形可得,展开图中三角形图案的顶点应与圆形的图案相对,而选项A,D与此不符,所以错误;
三角形图案所在的面应与圆形的图案所在的面相邻,而选项C与此也不符,正确的是B.
故选:B.
二.填空题(共5小题)
11.如图为某几何体的展开图,该几何体的名称是 圆柱 .
解:∵圆柱的展开图为两个圆和一个长方形,
∴展开图可得此几何体为圆柱.
故答案为:圆柱.
12.长方体纸盒的长、宽、高分别是10cm,8cm,5cm,若将它沿棱剪开,展成一个平面图形那么这个平面图形的周长的最小值是 92 cm.
解:如图所示:
这个平面图形的周长的最小值是:5×8+8×4+10×2=92(cm).
故答案为:92
13.一个圆柱的侧面展开后是一个边长为12.56cm的正方形,这个圆柱的底面半径是 2cm .
解:12.56÷3.14÷2=2(cm),
答:这个圆柱的底面半径是2cm.
故答案为:2cm.
14.如图1,在长为a,宽为b的长方形的四个角,各剪去一个边长为x的小正方形,从而折成如图2的长方体盒子,则用代数式表示图1中阴影部分的面积为 4x2﹣2x(a+b)+ab .
解:S=(a﹣2x)(b﹣2x)
=4x2﹣2ax﹣2bx+ab
=4x2﹣2x(a+b)+ab,
所以阴影部分的面积为4x2﹣2x(a+b)+ab,
故答案为:4x2﹣2x(a+b)+ab.
15.如图,将一张长为17,宽为11的长方形纸片,去掉阴影部分,恰可以围成一个宽是高2倍的长方体纸盒,这个长方体纸盒的容积是 56 .
解:设长为y,高为x,则宽为2x,依题意得
,
解得,
∴这个长方体纸盒的容积是4×2×7=56,
故答案为:56.
三.解答题(共5小题)
16.已知一个六棱柱,它的底面边长都是5厘米,侧棱长都是8厘米,请回答下列问题
(1)这个六棱柱一共有多少个面?一共有多少条棱?这些棱的长度之和是多少?
(2)沿一条侧棱将这个六棱柱侧面全部展开成一个平面图形,这个图形的面积是多少?
解:(1)这个六棱柱一共有2+6=8个面;一共有6×3=18条棱;这些棱的长度之和是8×6+5×6×2=108厘米;
(2)侧面全部展开成一个平面图形,其面积为8×5×6=240厘米2.
17.图1所示的三棱柱,高为7cm,底面是一个边长为5cm的等边三角形.
(1)这个三棱柱有 9 条棱,有 5 个面;
(2)图2方框中的图形是该三棱柱的表面展开图的一部分,请将它补全;
(3)要将该三棱柱的表面沿某些棱剪开,展开成一个平面图形,需剪开 5 条棱,需剪开棱的棱长的和的最大值为 31 cm.
解:(1)这个三棱柱有条9棱,有个5面;
故答案为:9,5;
(2)如图;
(3)由图形可知:没有剪开的棱的条数是4条,
则至少需要剪开的棱的条数是:9﹣4=5(条).
故至少需要剪开的棱的条数是5条.
需剪开棱的棱长的和的最大值为:7×3+5×2=31(cm).
故答案为:5,31.
18.如图是由小正方形组成的图,请你用三种方法分别在下图中添画两个小正方形,使它能成为正方体的表面展开图.
解:如图所示:
19.如图所示,两个圆和一个长方形(阴影部分)恰好可以围成一个圆柱,求这个圆柱的体积(π取3.14).
解:由图可知,圆柱的半径r=12.56÷(2π)=2(dm),高h=4r=8dm,
则体积V=πr2h=3.14×22×8=100.48(dm3).
答:这个圆柱的体积是100.48dm3.
20.(1)如图1所示的四个图分别由六个相同的正方形拼接而成,其中不能折成正方体的是 D .
(2)用斜二测画法补画图2,使它成为长方体的直观图.(注:遮住的线段用虚线表示,保留痕迹,不必写画法)
(3)在这一长方体中,从同一个顶点出发的三个面的面积之比为5:7:2,其中最大的面积比最小的面积大30cm2,求这个长方体的表面积.
解:(1)D
不能折成正方体,
故答案为:D;
(2)作图如图:
(3)设这三个面的面积分别为5xcm2、7xcm2、2xcm2,
7x﹣2x=30,
x=6,
2×(5×6+7×6+2×6)=168(cm2).
答:这个长方体的表面积是168cm2.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
4.4
课题学习
设计制作长方体形状的包装纸盒
高频易错题集
一.选择题(共10小题)
1.如图是某个几何体的展开图,该几何体是( )
A.三棱柱
B.三棱锥
C.圆柱
D.圆锥
2.正方体展开后,不能得到的展开图是( )
A.
B.
C.
D.
3.一个正方体的表面展开图可以是下列图形中的( )
A.
B.
C.
D.
4.如图正方体纸盒,展开后可以得到( )
A.
B.
C.
D.
5.下列图形中,不是正方体的展开图的是( )
A.
B.
C.
D.
6.从如图所示的7个小正方形中剪去一个小正方形,使剩余的6个小正方形折叠后能围成一个正方体,则应剪去标记为( )的小正方形
A.祝或考
B.你或考
C.好或绩
D.祝或你或成
7.如图所示的纸片折成一个长方体纸盒,折得的纸盒是( )
A.
B.
C.
D.
8.下列平面图形中,经过折叠不能围成正方体的是( )
A.
B.
C.
D.
9.下列图形,折叠后不能围成正方体的是( )
A.
B.
C.
D.
10.下面四个图形中,经过折叠能围成如图所示的几何图形的是( )
A.
B.
C.
D.
二.填空题(共5小题)
11.如图为某几何体的展开图,该几何体的名称是
.
12.长方体纸盒的长、宽、高分别是10cm,8cm,5cm,若将它沿棱剪开,展成一个平面图形那么这个平面图形的周长的最小值是
cm.
13.一个圆柱的侧面展开后是一个边长为12.56cm的正方形,这个圆柱的底面半径是
.
14.如图1,在长为a,宽为b的长方形的四个角,各剪去一个边长为x的小正方形,从而折成如图2的长方体盒子,则用代数式表示图1中阴影部分的面积为
.
15.如图,将一张长为17,宽为11的长方形纸片,去掉阴影部分,恰可以围成一个宽是高2倍的长方体纸盒,这个长方体纸盒的容积是
.
三.解答题(共5小题)
16.已知一个六棱柱,它的底面边长都是5厘米,侧棱长都是8厘米,请回答下列问题
(1)这个六棱柱一共有多少个面?一共有多少条棱?这些棱的长度之和是多少?
(2)沿一条侧棱将这个六棱柱侧面全部展开成一个平面图形,这个图形的面积是多少?
17.图1所示的三棱柱,高为7cm,底面是一个边长为5cm的等边三角形.
(1)这个三棱柱有
条棱,有
个面;
(2)图2方框中的图形是该三棱柱的表面展开图的一部分,请将它补全;
(3)要将该三棱柱的表面沿某些棱剪开,展开成一个平面图形,需剪开
条棱,需剪开棱的棱长的和的最大值为
cm.
18.如图是由小正方形组成的图,请你用三种方法分别在下图中添画两个小正方形,使它能成为正方体的表面展开图.
19.如图所示,两个圆和一个长方形(阴影部分)恰好可以围成一个圆柱,求这个圆柱的体积(π取3.14).
20.(1)如图1所示的四个图分别由六个相同的正方形拼接而成,其中不能折成正方体的是
.
(2)用斜二测画法补画图2,使它成为长方体的直观图.(注:遮住的线段用虚线表示,保留痕迹,不必写画法)
(3)在这一长方体中,从同一个顶点出发的三个面的面积之比为5:7:2,其中最大的面积比最小的面积大30cm2,求这个长方体的表面积.
试题解析
一.选择题(共10小题)
1.如图是某个几何体的展开图,该几何体是( )
A.三棱柱
B.三棱锥
C.圆柱
D.圆锥
解:观察图形可知,这个几何体是三棱柱.
故选:A.
2.正方体展开后,不能得到的展开图是( )
A.
B.
C.
D.
解:选项B、C、D都能折叠成正方体,只有选项A中,出现“田”字形,不能折成正方体.
故选:A.
3.一个正方体的表面展开图可以是下列图形中的( )
A.
B.
C.
D.
解:A,C,D折叠后有一行两个面无法折起来,从而缺少面,不能折成正方体,只有B是一个正方体的表面展开图.
故选:B.
4.如图正方体纸盒,展开后可以得到( )
A.
B.
C.
D.
解:A.两个蓝色圆所在的面折叠后是对面,不合题意;
B.白色圆与一个蓝色圆所在的面折叠后是对面,不合题意;
C.白色圆与一个蓝色圆所在的面折叠后是对面,不合题意;
D.白色圆与两个蓝色圆所在的面折叠后是相邻的面,符合题意;
故选:D.
5.下列图形中,不是正方体的展开图的是( )
A.
B.
C.
D.
解:A、B、D可组成正方体;
C不能组成正方体.
故选:C.
6.从如图所示的7个小正方形中剪去一个小正方形,使剩余的6个小正方形折叠后能围成一个正方体,则应剪去标记为( )的小正方形
A.祝或考
B.你或考
C.好或绩
D.祝或你或成
解:由图可得,与“绩”相对的面不唯一,与“出”相对的面不唯一,
将如图所示的图形剪去一个小正方形,使余下的部分恰好能折成一个正方体,应剪去标记为祝或你或成的小正方形,
故选:D.
7.如图所示的纸片折成一个长方体纸盒,折得的纸盒是( )
A.
B.
C.
D.
解:如图所示:
根据题意可知,A的对面是A′,B的对面是B′,C的对面是C′,A的短边阴影与C的阴影重合.
故用形如图所示的纸片折成一个长方体纸盒,折得的纸盒是C.
故选:C.
8.下列平面图形中,经过折叠不能围成正方体的是( )
A.
B.
C.
D.
解:由展开图可知:A、B、D能围成正方体,故不符合题意;
C、围成几何体时,有两个面重合,不能围成正方体,故符合题意.
故选:C.
9.下列图形,折叠后不能围成正方体的是( )
A.
B.
C.
D.
解:由展开图可知:A、B、C能围成正方体,不符合题意;
D、是“田”字形,围成几何体时,有两个面重合,故不能围成正方体,符合题意.
故选:D.
10.下面四个图形中,经过折叠能围成如图所示的几何图形的是( )
A.
B.
C.
D.
解:根据立体图形可得,展开图中三角形图案的顶点应与圆形的图案相对,而选项A,D与此不符,所以错误;
三角形图案所在的面应与圆形的图案所在的面相邻,而选项C与此也不符,正确的是B.
故选:B.
二.填空题(共5小题)
11.如图为某几何体的展开图,该几何体的名称是 圆柱 .
解:∵圆柱的展开图为两个圆和一个长方形,
∴展开图可得此几何体为圆柱.
故答案为:圆柱.
12.长方体纸盒的长、宽、高分别是10cm,8cm,5cm,若将它沿棱剪开,展成一个平面图形那么这个平面图形的周长的最小值是 92 cm.
解:如图所示:
这个平面图形的周长的最小值是:5×8+8×4+10×2=92(cm).
故答案为:92
13.一个圆柱的侧面展开后是一个边长为12.56cm的正方形,这个圆柱的底面半径是 2cm .
解:12.56÷3.14÷2=2(cm),
答:这个圆柱的底面半径是2cm.
故答案为:2cm.
14.如图1,在长为a,宽为b的长方形的四个角,各剪去一个边长为x的小正方形,从而折成如图2的长方体盒子,则用代数式表示图1中阴影部分的面积为 4x2﹣2x(a+b)+ab .
解:S=(a﹣2x)(b﹣2x)
=4x2﹣2ax﹣2bx+ab
=4x2﹣2x(a+b)+ab,
所以阴影部分的面积为4x2﹣2x(a+b)+ab,
故答案为:4x2﹣2x(a+b)+ab.
15.如图,将一张长为17,宽为11的长方形纸片,去掉阴影部分,恰可以围成一个宽是高2倍的长方体纸盒,这个长方体纸盒的容积是 56 .
解:设长为y,高为x,则宽为2x,依题意得
,
解得,
∴这个长方体纸盒的容积是4×2×7=56,
故答案为:56.
三.解答题(共5小题)
16.已知一个六棱柱,它的底面边长都是5厘米,侧棱长都是8厘米,请回答下列问题
(1)这个六棱柱一共有多少个面?一共有多少条棱?这些棱的长度之和是多少?
(2)沿一条侧棱将这个六棱柱侧面全部展开成一个平面图形,这个图形的面积是多少?
解:(1)这个六棱柱一共有2+6=8个面;一共有6×3=18条棱;这些棱的长度之和是8×6+5×6×2=108厘米;
(2)侧面全部展开成一个平面图形,其面积为8×5×6=240厘米2.
17.图1所示的三棱柱,高为7cm,底面是一个边长为5cm的等边三角形.
(1)这个三棱柱有 9 条棱,有 5 个面;
(2)图2方框中的图形是该三棱柱的表面展开图的一部分,请将它补全;
(3)要将该三棱柱的表面沿某些棱剪开,展开成一个平面图形,需剪开 5 条棱,需剪开棱的棱长的和的最大值为 31 cm.
解:(1)这个三棱柱有条9棱,有个5面;
故答案为:9,5;
(2)如图;
(3)由图形可知:没有剪开的棱的条数是4条,
则至少需要剪开的棱的条数是:9﹣4=5(条).
故至少需要剪开的棱的条数是5条.
需剪开棱的棱长的和的最大值为:7×3+5×2=31(cm).
故答案为:5,31.
18.如图是由小正方形组成的图,请你用三种方法分别在下图中添画两个小正方形,使它能成为正方体的表面展开图.
解:如图所示:
19.如图所示,两个圆和一个长方形(阴影部分)恰好可以围成一个圆柱,求这个圆柱的体积(π取3.14).
解:由图可知,圆柱的半径r=12.56÷(2π)=2(dm),高h=4r=8dm,
则体积V=πr2h=3.14×22×8=100.48(dm3).
答:这个圆柱的体积是100.48dm3.
20.(1)如图1所示的四个图分别由六个相同的正方形拼接而成,其中不能折成正方体的是 D .
(2)用斜二测画法补画图2,使它成为长方体的直观图.(注:遮住的线段用虚线表示,保留痕迹,不必写画法)
(3)在这一长方体中,从同一个顶点出发的三个面的面积之比为5:7:2,其中最大的面积比最小的面积大30cm2,求这个长方体的表面积.
解:(1)D
不能折成正方体,
故答案为:D;
(2)作图如图:
(3)设这三个面的面积分别为5xcm2、7xcm2、2xcm2,
7x﹣2x=30,
x=6,
2×(5×6+7×6+2×6)=168(cm2).
答:这个长方体的表面积是168cm2.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
