教科版(2019)信息技术必修一 4.2 数值计算 教案(2课时)
文档属性
| 名称 | 教科版(2019)信息技术必修一 4.2 数值计算 教案(2课时) |  | |
| 格式 | docx | ||
| 文件大小 | 164.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 教科版(2019) | ||
| 科目 | 信息科技(信息技术) | ||
| 更新时间 | 2020-11-11 18:09:43 | ||
图片预览

文档简介
4.2 数值计算
【学习目标】
1.通过求解一元二次方程的解,了解计算机编程解决数值计算问题的一般流程,并能够使用解析法解决实际问题。
2.通过绘制一元多次方程函数图像,了解Python利用numpy和matplotlib两个模块绘制图像的基本方法。
3.通过编程求解一元多次方程,了解迭代法的含义,并尝试用牛顿迭代法解决实际问题。
【教学重点】
1.了解数值类算法在实际问题解决时的常用方法,如解析法和迭代法。
2.能够利用numpy和matplotlib两个模块绘制函数图像。
【教学难点】
理解迭代法的含义,并能够用牛顿迭代法求解一元多次方程。
【教学过程】
第一课时
师:计算机最初研究的用途就是进行数值计算,因此计算机可以解决很多数学方法所描绘的数值计算问题。本节将围绕项目“与数学公式面对面”探讨在中学数学领域里常见的数学公式与程序设计的有趣结合。完成下列的项目报告书。
与数学公式面对面
了解计算机进行数值计算的基本流程和方法。
环节一:求解一元二次方程ax2+bx+c=0(a≠0)
1.用数学方法求解方程2x2+x-6=0。
2.用WPS表格绘制方程2x2+x-6=0函数图象,求解方程。
3.用Python编程求解ax2+bx+c=0(a≠0)的解。a,b,c由程序输入。
与数学公式面对面
了解计算机进行数值计算的基本流程和方法。
环节一:求解一元二次方程ax2+bx+c=0(a≠0)
1.用数学方法求解方程2x2+x-6=0。
2.用WPS表格绘制方程2x2+x-6=0函数图象,求解方程。
3.用Python编程求解ax2+bx+c=0(a≠0)的解。a,b,c由程序输入。
完成项目报告书的过程中,比较数学方法、软件工具和编程解决问题的异同。
参考答案:
方法一:写出数学方法求解方程2x2+x-6=0。
方程可因式分解为(2x-3)(x+2)=0,因此x=1.5或x=-2。
用求根公式计算得x=1.5或x=-2。
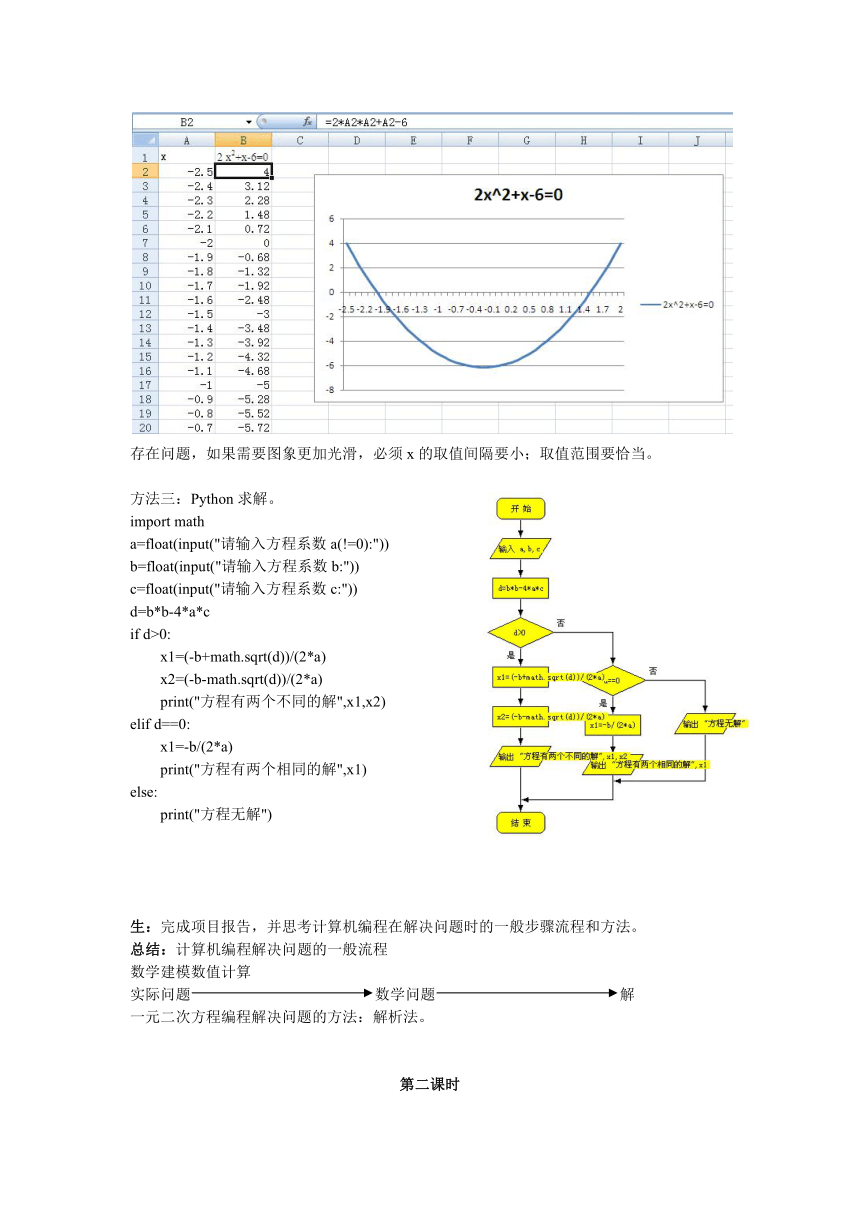
方法二:wps表格画图。
存在问题,如果需要图象更加光滑,必须x的取值间隔要小;取值范围要恰当。
285750051435
方法三:Python求解。
import math
a=float(input("请输入方程系数a(!=0):"))
b=float(input("请输入方程系数b:"))
c=float(input("请输入方程系数c:"))
d=b*b-4*a*c
if d>0:
x1=(-b+math.sqrt(d))/(2*a)
x2=(-b-math.sqrt(d))/(2*a)
print("方程有两个不同的解",x1,x2)
elif d==0:
x1=-b/(2*a)
print("方程有两个相同的解",x1)
else:
print("方程无解")
生:完成项目报告,并思考计算机编程在解决问题时的一般步骤流程和方法。
总结:计算机编程解决问题的一般流程
数学建模数值计算
实际问题数学问题解
一元二次方程编程解决问题的方法:解析法。
第二课时
一、引入
师:一元二次方程可以根据公式来直接求解,但一元多次方程没有现成的公式。可以利用绘制函数图像和编程实现问题的解决,完成项目报告。
与数学公式面对面
了解计算机进行数值计算的基本流程和方法。
环节二:求解一元多次方程x5+x4+x-3=0的解
1.利用Python绘制x5+x4+x-3=0在[-1,2]之间的函数图像。
2.用Python编程求解x5+x4+x-3=0。
与数学公式面对面
了解计算机进行数值计算的基本流程和方法。
环节二:求解一元多次方程x5+x4+x-3=0的解
1.利用Python绘制x5+x4+x-3=0在[-1,2]之间的函数图像。
2.用Python编程求解x5+x4+x-3=0。
为了完成该项目,必须学习如何利用Python绘制函数图像和编程求解一元多次方程。
二、Python绘制函数图像
师:在Python中绘制函数图像一般要用到numpy和matplotlib两个模块。
numpy是一个科学计算包。其中包含很多数学函数,如三角函数、矩阵计算方法等。通过该模块中的arange函数可以创建一个等差数列,也就是描点法中的取x值,然后用y=np.sin(x)计算y的值。
接着调用matplotlib模块绘制函数图像。调用matplotlib.pyplot在直角平面内轻松地将(x,y)坐标点对连接成平滑曲线。
那么绘制y=sin(x)函数的图像程序如下:
import numpy as np #加载numpy模块并取一个简洁的别名为np,便于后续引用
import matplotlib.pyplot as plt #加载matplotlib.pyplot并取别名为plt
x=np.arange(0,2*np.pi,0.01) #x在0到2π之间,每隔0.01取一个点
y=np.sin(x) #求sin(x)对应的y值
plt.plot(x,y) #绘制sin(x)图像,系统自动配置蓝色
plt.title('sin(x)') #设置图像标题
plt.xlabel('X') #设置X轴标题
plt.ylabel('Y') #设置Y轴标题
plt.show() #将绘制的函数图像窗口显示出来
练习:模仿绘制sin函数的方法,完成项目报告书,绘制x5+x4+x-10=0的图像。
生:
import numpy as np #加载numpy模块并取一个简洁的别名为np,便于后续引用
import matplotlib.pyplot as plt #加载matplotlib.pyplot并取别名为plt
x=np.arange(-1,2,0.01) #x在-1,2之间,每隔0.01取一个点
y=x**5+x**4+x-3 #求对应的y值
plt.plot(x,y) #绘制图像,系统自动配置蓝色
plt.title('x^5+x^4+x-3') #设置图像标题
plt.xlabel('X') #设置X轴标题
plt.ylabel('Y') #设置Y轴标题
plt.show() #将绘制的函数图像窗口显示出来
师:请同学们根据函数图像估算函数的解是多少?
三、编程求解一元多次方程
师:在解决该问题时,我们将引入一个新的算法:迭代法。迭代法也称辗转法,是让计算机对一组指令(或一定步骤)进行重复执行,在每次执行这组指令(或这些步骤)时,都从变量的原值推出它的一个新值。其中牛顿迭代法是求解方程根的重要方法之一。
用牛顿迭代法求解x5+x4+x-3=0的步骤可以理解为:
1.选取x1=0作为方程的初始解(x0应选取在解附近,这个可以通过观察函数图像得到);
2.新解,其中f(x1)= x15+x14+x1-3,f'(x1)=5*x14+4*x13+1;
3.如果|x1-x2|<1e-10,则解为x2,否则x1=x2,跳转到(2)。
练习:利用牛顿迭代法求解方程x5+x4+x-3=0。
生:
def f(x):
#定义f(x)函数,计算f(x)=x**5+x**4+x-3
f=x**5+x**4+x-3
return f
def f1(x):
#定义f1(x)函数,计算f'(x)= 5*x**4+4*x**3+1
f1=5*(x**4)+4*(x**3)+1
return f1
x1=0.5 #x1,x2的初值只要确保|x1-x2|>1e-10就可以
x2=1.5 #解系列初值
print('迭代过程中的x值:')
#根据迭代公式计算
while abs(x1-x2)>1e-10:
print(x2)
x1=x2
x2=x1-f(x1)/f1(x1)
print('近似解:',x1) #输出最后解
input("运行完毕,请按回车键退出...")
运行结果
迭代过程中的x值:
1.5
1.2197802197802199
1.057644072697476
1.004898720733028
1.0000381246489294
1.0000000023254536
1.0
近似解:1.0
运行完毕,请按回车键退出...
总结:一元多次方程编程解决问题的方法:牛顿迭代法。
计算机编程解决问题的一般流程
数学建模数值计算
实际问题数学问题近似解
【学习目标】
1.通过求解一元二次方程的解,了解计算机编程解决数值计算问题的一般流程,并能够使用解析法解决实际问题。
2.通过绘制一元多次方程函数图像,了解Python利用numpy和matplotlib两个模块绘制图像的基本方法。
3.通过编程求解一元多次方程,了解迭代法的含义,并尝试用牛顿迭代法解决实际问题。
【教学重点】
1.了解数值类算法在实际问题解决时的常用方法,如解析法和迭代法。
2.能够利用numpy和matplotlib两个模块绘制函数图像。
【教学难点】
理解迭代法的含义,并能够用牛顿迭代法求解一元多次方程。
【教学过程】
第一课时
师:计算机最初研究的用途就是进行数值计算,因此计算机可以解决很多数学方法所描绘的数值计算问题。本节将围绕项目“与数学公式面对面”探讨在中学数学领域里常见的数学公式与程序设计的有趣结合。完成下列的项目报告书。
与数学公式面对面
了解计算机进行数值计算的基本流程和方法。
环节一:求解一元二次方程ax2+bx+c=0(a≠0)
1.用数学方法求解方程2x2+x-6=0。
2.用WPS表格绘制方程2x2+x-6=0函数图象,求解方程。
3.用Python编程求解ax2+bx+c=0(a≠0)的解。a,b,c由程序输入。
与数学公式面对面
了解计算机进行数值计算的基本流程和方法。
环节一:求解一元二次方程ax2+bx+c=0(a≠0)
1.用数学方法求解方程2x2+x-6=0。
2.用WPS表格绘制方程2x2+x-6=0函数图象,求解方程。
3.用Python编程求解ax2+bx+c=0(a≠0)的解。a,b,c由程序输入。
完成项目报告书的过程中,比较数学方法、软件工具和编程解决问题的异同。
参考答案:
方法一:写出数学方法求解方程2x2+x-6=0。
方程可因式分解为(2x-3)(x+2)=0,因此x=1.5或x=-2。
用求根公式计算得x=1.5或x=-2。
方法二:wps表格画图。
存在问题,如果需要图象更加光滑,必须x的取值间隔要小;取值范围要恰当。
285750051435
方法三:Python求解。
import math
a=float(input("请输入方程系数a(!=0):"))
b=float(input("请输入方程系数b:"))
c=float(input("请输入方程系数c:"))
d=b*b-4*a*c
if d>0:
x1=(-b+math.sqrt(d))/(2*a)
x2=(-b-math.sqrt(d))/(2*a)
print("方程有两个不同的解",x1,x2)
elif d==0:
x1=-b/(2*a)
print("方程有两个相同的解",x1)
else:
print("方程无解")
生:完成项目报告,并思考计算机编程在解决问题时的一般步骤流程和方法。
总结:计算机编程解决问题的一般流程
数学建模数值计算
实际问题数学问题解
一元二次方程编程解决问题的方法:解析法。
第二课时
一、引入
师:一元二次方程可以根据公式来直接求解,但一元多次方程没有现成的公式。可以利用绘制函数图像和编程实现问题的解决,完成项目报告。
与数学公式面对面
了解计算机进行数值计算的基本流程和方法。
环节二:求解一元多次方程x5+x4+x-3=0的解
1.利用Python绘制x5+x4+x-3=0在[-1,2]之间的函数图像。
2.用Python编程求解x5+x4+x-3=0。
与数学公式面对面
了解计算机进行数值计算的基本流程和方法。
环节二:求解一元多次方程x5+x4+x-3=0的解
1.利用Python绘制x5+x4+x-3=0在[-1,2]之间的函数图像。
2.用Python编程求解x5+x4+x-3=0。
为了完成该项目,必须学习如何利用Python绘制函数图像和编程求解一元多次方程。
二、Python绘制函数图像
师:在Python中绘制函数图像一般要用到numpy和matplotlib两个模块。
numpy是一个科学计算包。其中包含很多数学函数,如三角函数、矩阵计算方法等。通过该模块中的arange函数可以创建一个等差数列,也就是描点法中的取x值,然后用y=np.sin(x)计算y的值。
接着调用matplotlib模块绘制函数图像。调用matplotlib.pyplot在直角平面内轻松地将(x,y)坐标点对连接成平滑曲线。
那么绘制y=sin(x)函数的图像程序如下:
import numpy as np #加载numpy模块并取一个简洁的别名为np,便于后续引用
import matplotlib.pyplot as plt #加载matplotlib.pyplot并取别名为plt
x=np.arange(0,2*np.pi,0.01) #x在0到2π之间,每隔0.01取一个点
y=np.sin(x) #求sin(x)对应的y值
plt.plot(x,y) #绘制sin(x)图像,系统自动配置蓝色
plt.title('sin(x)') #设置图像标题
plt.xlabel('X') #设置X轴标题
plt.ylabel('Y') #设置Y轴标题
plt.show() #将绘制的函数图像窗口显示出来
练习:模仿绘制sin函数的方法,完成项目报告书,绘制x5+x4+x-10=0的图像。
生:
import numpy as np #加载numpy模块并取一个简洁的别名为np,便于后续引用
import matplotlib.pyplot as plt #加载matplotlib.pyplot并取别名为plt
x=np.arange(-1,2,0.01) #x在-1,2之间,每隔0.01取一个点
y=x**5+x**4+x-3 #求对应的y值
plt.plot(x,y) #绘制图像,系统自动配置蓝色
plt.title('x^5+x^4+x-3') #设置图像标题
plt.xlabel('X') #设置X轴标题
plt.ylabel('Y') #设置Y轴标题
plt.show() #将绘制的函数图像窗口显示出来
师:请同学们根据函数图像估算函数的解是多少?
三、编程求解一元多次方程
师:在解决该问题时,我们将引入一个新的算法:迭代法。迭代法也称辗转法,是让计算机对一组指令(或一定步骤)进行重复执行,在每次执行这组指令(或这些步骤)时,都从变量的原值推出它的一个新值。其中牛顿迭代法是求解方程根的重要方法之一。
用牛顿迭代法求解x5+x4+x-3=0的步骤可以理解为:
1.选取x1=0作为方程的初始解(x0应选取在解附近,这个可以通过观察函数图像得到);
2.新解,其中f(x1)= x15+x14+x1-3,f'(x1)=5*x14+4*x13+1;
3.如果|x1-x2|<1e-10,则解为x2,否则x1=x2,跳转到(2)。
练习:利用牛顿迭代法求解方程x5+x4+x-3=0。
生:
def f(x):
#定义f(x)函数,计算f(x)=x**5+x**4+x-3
f=x**5+x**4+x-3
return f
def f1(x):
#定义f1(x)函数,计算f'(x)= 5*x**4+4*x**3+1
f1=5*(x**4)+4*(x**3)+1
return f1
x1=0.5 #x1,x2的初值只要确保|x1-x2|>1e-10就可以
x2=1.5 #解系列初值
print('迭代过程中的x值:')
#根据迭代公式计算
while abs(x1-x2)>1e-10:
print(x2)
x1=x2
x2=x1-f(x1)/f1(x1)
print('近似解:',x1) #输出最后解
input("运行完毕,请按回车键退出...")
运行结果
迭代过程中的x值:
1.5
1.2197802197802199
1.057644072697476
1.004898720733028
1.0000381246489294
1.0000000023254536
1.0
近似解:1.0
运行完毕,请按回车键退出...
总结:一元多次方程编程解决问题的方法:牛顿迭代法。
计算机编程解决问题的一般流程
数学建模数值计算
实际问题数学问题近似解
