五年级上册数学课件 第6单元《第3课时 梯形的面积》人教版 (共19张PPT)
文档属性
| 名称 | 五年级上册数学课件 第6单元《第3课时 梯形的面积》人教版 (共19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-11 20:13:23 | ||
图片预览




文档简介
第6单元 多边形的面积
第3课时 梯形的面积
人教版数学五年级上册
学习目标
1.运用转化的数学思想,用多种方法探索并掌握梯形面积公式,能解决相关的问题,综合了解平面图形的内在联系。
2.在观察、推理、归纳的能力中提高学生的动手能力和知识迁移能力,体会转化思想的价值。
3.进一步积累解决问题的经验,增强新图形面积研究的策略意识,获得成功体验,提高学习自信心。
导入新知
1.平行四边形的面积公式是怎样的?
2.三角形的面积公式是怎样的?它是通过怎样的转化推导出来的?为什么要“÷2”?
3.求下列图形的面积。
(1)已知平行四边形的底是3米,高是2米。求面积。
(2)已知三角形的底是4米,高是5米。求面积。
车窗玻璃的形状是梯形!怎样求出它的面积呢?
你能用学过的方法推导出梯形的面积计算公式吗?
阅读与理解
合作探究
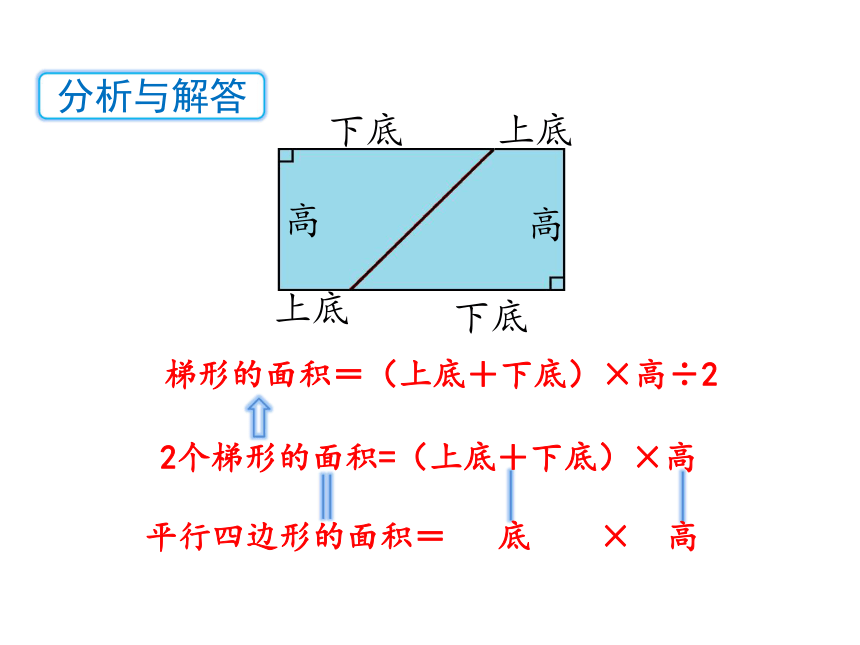
分析与解答
上底
高
下底
上底
高
下底
梯形的面积=(上底+下底)×高÷2
平行四边形的面积= 底 × 高
2个梯形的面积=(上底+下底)×高
分析与解答
上底
高
下底
上底
高
下底
梯形的面积=(上底+下底)×高÷2
平行四边形的面积= 底 × 高
2个梯形的面积=(上底+下底)×高
分析与解答
上底
高
下底
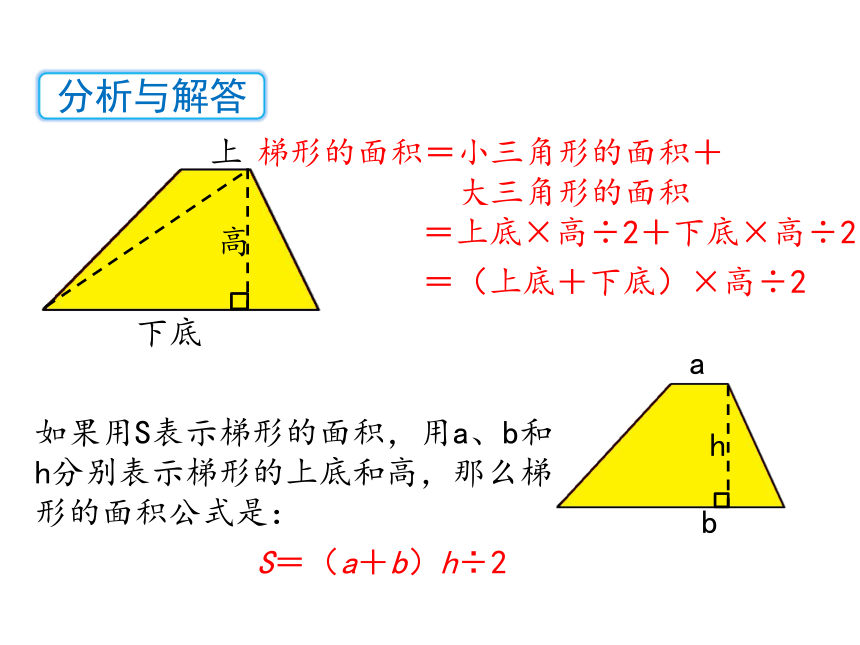
梯形的面积=小三角形的面积+
大三角形的面积
=上底×高÷2+下底×高÷2
=(上底+下底)×高÷2
a
b
h
如果用S表示梯形的面积,用a、b和h分别表示梯形的上底和高,那么梯形的面积公式是:
S=(a+b)h÷2
例题练习
题目中给出了梯形的上底、下底和高,可以根据梯形的面积计算公式直接列式计算。
我国三峡水电站大坝的横截面的一部分是梯形(如下图),求它的面积。
规范解答
S=(a+b)h÷2
=(36+120)×135÷2
=156×135÷2
=10530(m2)
答:三峡水电站大坝的横截面梯形部分
的面积是10563m2
1.一辆汽车侧面的两块玻璃的形状是梯形(如下图),它们的面积分别是多少?
S=(a+b)h÷2
=(40+71)×40÷2
=111×40÷2
=2220(cm2)
S=(a+b)h÷2
=(45+65)×40÷2
=110×40÷2
=2200(cm2)
典型例题
2.一个剧场设置了40排座位,第一排有76个座位,往后逐排比前一排多2个座位,最后一排有152个座位,这个剧场一共设置了多少个座位?
解:(76+152)×40 ÷ 2=4560(个)
答:这个剧场一共设置了4560个座位。
课堂练习
1.已知梯形的上底、下底和高,可以直
接利用公式求出梯形的面积。
2.计算梯形面积时不要忘了除以2。
归纳新知
再 见
第3课时 梯形的面积
人教版数学五年级上册
学习目标
1.运用转化的数学思想,用多种方法探索并掌握梯形面积公式,能解决相关的问题,综合了解平面图形的内在联系。
2.在观察、推理、归纳的能力中提高学生的动手能力和知识迁移能力,体会转化思想的价值。
3.进一步积累解决问题的经验,增强新图形面积研究的策略意识,获得成功体验,提高学习自信心。
导入新知
1.平行四边形的面积公式是怎样的?
2.三角形的面积公式是怎样的?它是通过怎样的转化推导出来的?为什么要“÷2”?
3.求下列图形的面积。
(1)已知平行四边形的底是3米,高是2米。求面积。
(2)已知三角形的底是4米,高是5米。求面积。
车窗玻璃的形状是梯形!怎样求出它的面积呢?
你能用学过的方法推导出梯形的面积计算公式吗?
阅读与理解
合作探究
分析与解答
上底
高
下底
上底
高
下底
梯形的面积=(上底+下底)×高÷2
平行四边形的面积= 底 × 高
2个梯形的面积=(上底+下底)×高
分析与解答
上底
高
下底
上底
高
下底
梯形的面积=(上底+下底)×高÷2
平行四边形的面积= 底 × 高
2个梯形的面积=(上底+下底)×高
分析与解答
上底
高
下底
梯形的面积=小三角形的面积+
大三角形的面积
=上底×高÷2+下底×高÷2
=(上底+下底)×高÷2
a
b
h
如果用S表示梯形的面积,用a、b和h分别表示梯形的上底和高,那么梯形的面积公式是:
S=(a+b)h÷2
例题练习
题目中给出了梯形的上底、下底和高,可以根据梯形的面积计算公式直接列式计算。
我国三峡水电站大坝的横截面的一部分是梯形(如下图),求它的面积。
规范解答
S=(a+b)h÷2
=(36+120)×135÷2
=156×135÷2
=10530(m2)
答:三峡水电站大坝的横截面梯形部分
的面积是10563m2
1.一辆汽车侧面的两块玻璃的形状是梯形(如下图),它们的面积分别是多少?
S=(a+b)h÷2
=(40+71)×40÷2
=111×40÷2
=2220(cm2)
S=(a+b)h÷2
=(45+65)×40÷2
=110×40÷2
=2200(cm2)
典型例题
2.一个剧场设置了40排座位,第一排有76个座位,往后逐排比前一排多2个座位,最后一排有152个座位,这个剧场一共设置了多少个座位?
解:(76+152)×40 ÷ 2=4560(个)
答:这个剧场一共设置了4560个座位。
课堂练习
1.已知梯形的上底、下底和高,可以直
接利用公式求出梯形的面积。
2.计算梯形面积时不要忘了除以2。
归纳新知
再 见
