2020-2021学年青岛新版九年级上册数学《第2章 解直角三角形》单元测试卷(Word版 含解析)
文档属性
| 名称 | 2020-2021学年青岛新版九年级上册数学《第2章 解直角三角形》单元测试卷(Word版 含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 398.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-11 22:59:42 | ||
图片预览



文档简介
2020-2021学年青岛新版九年级上册数学《第2章
解直角三角形》单元测试卷
一.选择题(共10小题)
1.△ABC的周长为36cm,∠C=90°,tanA=,则△ABC的面积是( )
A.30cm2
B.54cm2
C.60cm2
D.108cm2
2.若0°<α<45°,则下列各式中正确的是( )
A.sinα>cosα
B.cosα>sinα
C.cotα<1
D.tanα>cotα
3.若tanα=2,则的值为( )
A.
B.
C.
D.1
4.若α是直角三角形的一个锐角,且cosα=sin40°,则α的度数为( )
A.20°
B.30°
C.40°
D.50°
5.若2cosα﹣=0,则锐角α=( )
A.30°
B.15°
C.45°
D.60°
6.用计算器求sin20°+tan54°33′的结果等于(结果精确到0.01)( )
A.2.25
B.1.55
C.1.73
D.1.75
7.如图,∠α的顶点在坐标原点,始边与x轴的正半轴重合,终边上一点的横坐标是3,且tanα=,则OP=( )
A.3
B.4
C.
D.5
8.如图,C、D、B在同一直线上,∠ACB=30°,∠ADB=45°,CD=14,∠ABC=90°.那么AB=( )
A.
+7
B.
+7
C.﹣7
D.
+7
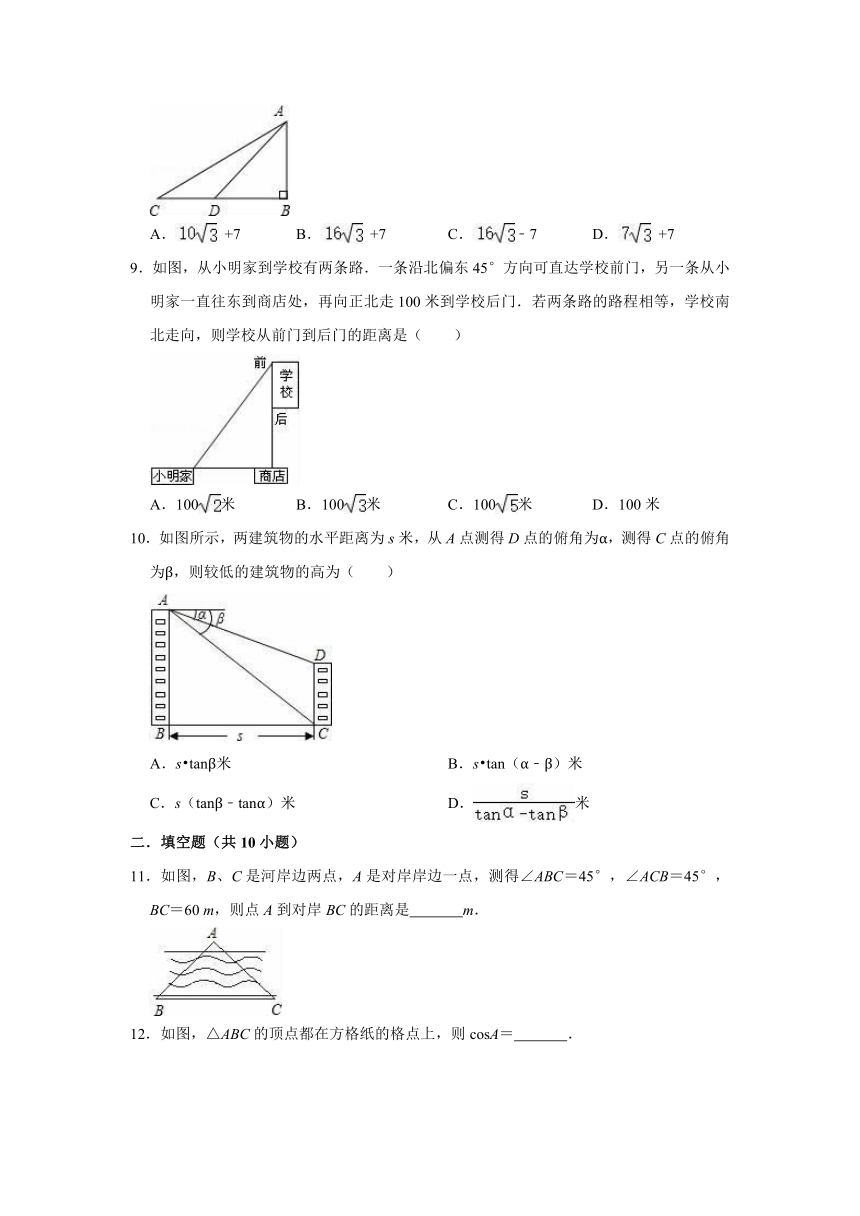
9.如图,从小明家到学校有两条路.一条沿北偏东45°方向可直达学校前门,另一条从小明家一直往东到商店处,再向正北走100米到学校后门.若两条路的路程相等,学校南北走向,则学校从前门到后门的距离是( )
A.100米
B.100米
C.100米
D.100米
10.如图所示,两建筑物的水平距离为s米,从A点测得D点的俯角为α,测得C点的俯角为β,则较低的建筑物的高为( )
A.s?tanβ米
B.s?tan(α﹣β)米
C.s(tanβ﹣tanα)米
D.米
二.填空题(共10小题)
11.如图,B、C是河岸边两点,A是对岸岸边一点,测得∠ABC=45°,∠ACB=45°,BC=60
m,则点A到对岸BC的距离是
m.
12.如图,△ABC的顶点都在方格纸的格点上,则cosA=
.
13.用“>”或“<”连结:
cos18°
cos18°3′;
tan31°
tan32°;
tan29°30′
cot60°29′;
sin39°
cos51°;
cot30°
sin89°;
sinα+cosα
1(α为锐角)
14.用计算器计算:sin35°≈
(结果保留两个有效数字).
15.周长为22的等腰三角形,一边长为8,则底角的余弦值为
.
16.某校数学兴趣小组在测量一座池塘边上A,B两点间的距离时用了以下三种测量方法,如图所示.图中a,b,c表示长度,β表示角度.请你求出AB的长度(用含有a,b,c,β字母的式子表示).
(1)AB=
;(2)AB=
;(3)AB=
.
17.在一坡比为1:7的斜坡上种有两棵小树,它们之间的距离AB为10米,则这两棵树的高度差BC为
米.
18.△ABC中,∠C=90°,cosA=,sinB=|n|﹣,则n=
.
19.在△ABC中,∠A,∠B都是锐角,且满足|sinA﹣|+(﹣cosB)2=0,则∠C的度数为
.
20.如图,某飞机于空中探测某座山的高度,在点A处飞机的飞行高度是AF=3700米,从飞机上观测山顶目标C的俯角是45°,飞机继续以相同的高度飞行300米到B地,此时观察目标C的俯角是50°,则这座山的高度CD是
米(参考数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.20)
三.解答题(共7小题)
21.计算:
(1)sin60°+
cos45°+sin30°?cos30°;
(2)3tan30°﹣+cos0°?cos45°;
(3)+;
(4)cos21°+cos22°+…+cos288°+cos289°.
22.△ABC中,∠BAC=90°,AD是高,BD=9,tanB=,求AD、AC、BC.
23.如图,河流的两岸MN、PQ互相平行,河岸PQ上有一排间隔为50m的电线杆C、D、E….某人在河岸MN的A处测得∠DAN=38°,然后沿河岸走了120m到达B处,测得∠CBN=70°.求河流的宽度CF.(结果精确到0.1m,参考数据:sin38°≈0.62,cos38°≈0.79,tan38°≈0.78,sin70°≈0.94,cos70°≈0.34,tan70°≈2.75)
24.如图,新华都超市的自动扶梯AB段的长度为20米,倾斜角为9°,求扶梯的高度BC为多少米?(精确到0.1米)
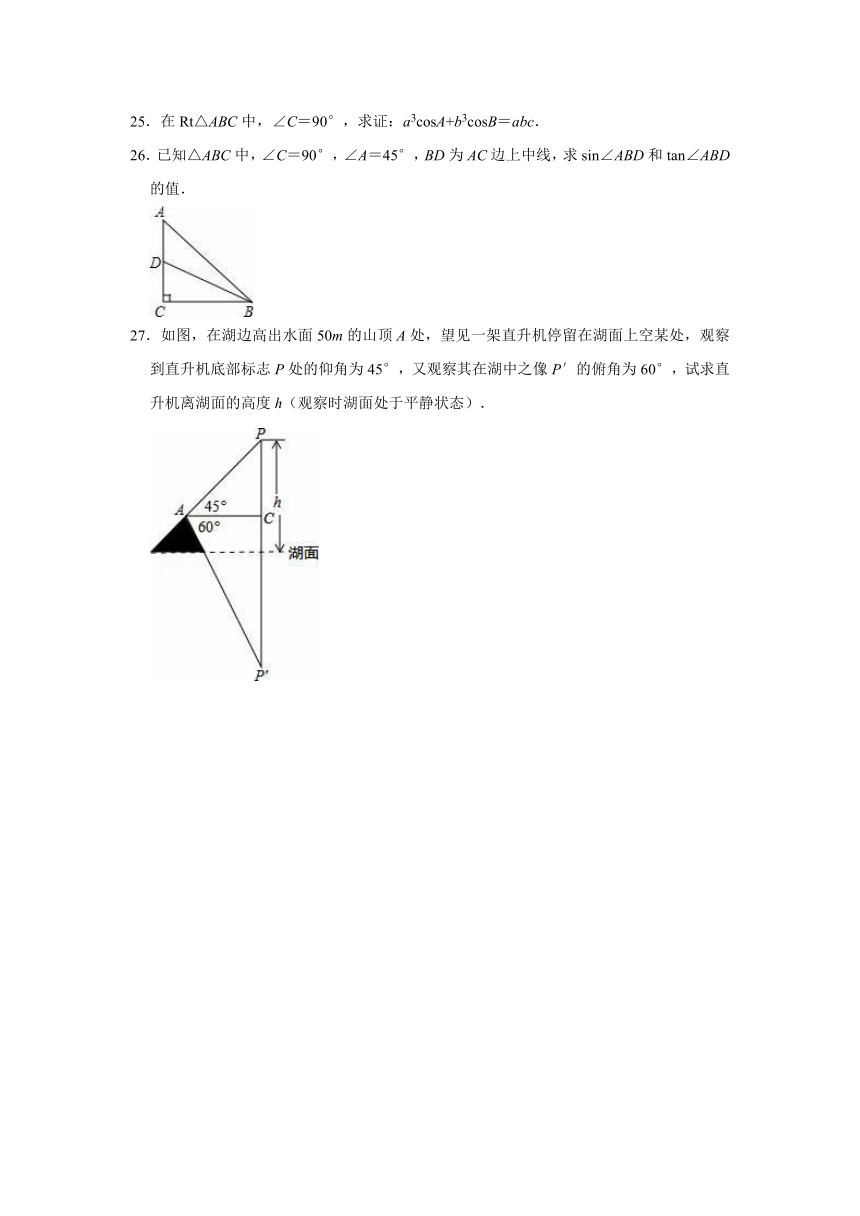
25.在Rt△ABC中,∠C=90°,求证:a3cosA+b3cosB=abc.
26.已知△ABC中,∠C=90°,∠A=45°,BD为AC边上中线,求sin∠ABD和tan∠ABD的值.
27.如图,在湖边高出水面50m的山顶A处,望见一架直升机停留在湖面上空某处,观察到直升机底部标志P处的仰角为45°,又观察其在湖中之像P′的俯角为60°,试求直升机离湖面的高度h(观察时湖面处于平静状态).
参考答案与试题解析
一.选择题(共10小题)
1.解:∵tanA==,
∴设AC=3x,则BC=4x,
根据勾股定理可以得到:AB=5x,
则3x+4x+5x=36,
解得:x=3,
则AC=9cm,BC=12cm,AB=15cm.
则△ABC的面积是:
AC?BC=×9×12=54cm2.
故选:B.
2.解:∵0°<α<45°,
∴sinα<sin(90°﹣α)=cosα,
∵tan45°=cot45°=1,
∴cotα>1,tanα<1,
∴cotα>tanα.
故选:B.
3.解:因为tanα==2,
∴原式====.
故选:C.
4.解:∵cosα=sin40°,
∴α=90°﹣40°=50°.
故选:D.
5.解:∵2cosα﹣=0,
∴cosα=,
∴α=30°.
故选:A.
6.解:sin20°+tan54°33′
=sin20°+tan54.55°
=0.3420+1.4045
=1.7465
≈1.75.
故选:D.
7.解:∵tanα==,
∴P点的纵坐标为3tanα=3×=4.
OP的长为.
故选:D.
8.解:在Rt△ABD中,tan∠ADB=,故AB=BD.
在Rt△ACB中,tan∠ACB=,
解得AB=7.
故选:D.
9.解:如图,由题意得∠DAB=45°,BC=100,AB+100=AD,
∵cos∠DAB==,
∴AB=AD=(AB+100),
解得:AB=100+100,
∴BD=AB=100+100,
∴CD=100(米).
故选:A.
10.解:作AE∥BC,与CD延长线相交于E点.
由于两建筑物的水平距离为s米,从A点测得D点的俯角为α,测得C点的俯角为β,
在Rt△ACE中,CE=tanβ?s;
在Rt△ADE中,DE=tanα?s,
则CD=s(tanβ﹣tanα).
故选:C.
二.填空题(共10小题)
11.解:由题意可得:∠A=180°﹣45°﹣45°=90°,
AB=AC=BC×sin45°=30.
∵面积S=AB×AC=BC×h,
∴h=30.
故点A到对岸BC的距离是30米.
12.解:
从图形可知:AE=4,CE=2,
由勾股定理得:AC=,
cosA===,
故答案为:.
13.解:cos18°>cos18°3′;
tan31°<tan32°;
tan29°30′<cot60°29′(cot60°29′=tan29°31′);
sin39°=cos51°(cos51°=sin39°);
cot30°>sin89°(cot30°>cot45°=1);
sinα+cosα>1(α为锐角).
故答案为>、<、<、=、>、>.
14.解:sin35°≈0.5736≈0.57.
故答案为:0.57.
15.解:作AD⊥BC于D,
当腰长AB=8时,底边长BC=6,
则BD=BC=3,
cosB==;
当底边长BC=8时,腰长AB=7,
则BD=BC=4,
cosB==,
故答案为:或.
16.解:(1)在直角△ABC中,AB=;
(2)在直角△ABC中,AB=a?tanβ;
(3)△ABC∽△EDC,
∴=,求得AB=.
故答案为:、a?tanβ、.
17.解:由题意,BC:AC=1:7,
在Rt△ABC中,AB=10m,
设BC=xm,则AC=7xm,
∴x2+49x2=100,
解得,x=(m),
∴BC=m.
故答案为:.
18.解:在△ABC中,∠C=90°,
∴∠A+∠B=90°,
∴sinB=cosA,
∴|n|﹣=,
∴|n|=1,
∴n=±1.
故答案为±1.
19.解:∵|sinA﹣|+(﹣cosB)2=0,
∴sinA=,cosB=.
∴∠A=45°,∠B=30°.
由三角形的内角和是180°可知∠C=180°﹣30°﹣45°=105°.
故答案为:105°.
20.解:设EC=x,
在Rt△BCE中,tan∠EBC=,
则BE==x,
在Rt△ACE中,tan∠EAC=,
则AE==x,
∵AB+BE=AE,
∴300+x=x,
解得:x=1800,
这座山的高度CD=DE﹣EC=3700﹣1800=1900(米).
故答案为:1900.
三.解答题(共7小题)
21.(1)sin60°+
cos45°+sin30°?cos30°;
=×+×+×,
=+
(2)3tan30°﹣+cos0°?cos45°;
=3×﹣(﹣1)+1×,
=﹣+1+,
=1+,
(3)+;
=+,
=1﹣﹣,
=﹣﹣,
(4)cos21°+cos22°+…+cos288°+cos289°.
=(cos21°+cos289°)+(cos22°+cos288°)+…cos245°,
=(cos21°+sin21°)+(cos22°+sin22°)+…cos245°,
=1+1+…+,
=44.
22.解:如图所示:∵∠ADB=90°,tanB=,BD=9,
∴tanB===,
解得:AD=12,
故AB==15,
tanB===,
解得:AC=20,
故BC==25.
23.解:过点C作CG∥DA交AB于点G.
∵MN∥PQ,CG∥DA,
∴四边形AGCD是平行四边形.
∴AG=CD=50m,∠CGB=38°.
∴GB=AB﹣AG=120﹣50=70(m).
∴tan38°==0.78,
在Rt△BFC中,
tan70°==2.75,
∴BF=,
∴==0.78,
解得:CF≈76.2(m).
答:河流的宽是76.2米.
24.解:由题意,在Rt△ABC中,
∠A=9°,有三角函数关系可知,
BC=AB?sinα=3.1米
即扶梯的高度约为3.1米.
25.证明:如图,cosA=,cosB=,
由勾股定理得,a2+b2=c2,
所以a3?+b3?=(a2+b2)=?c2=abc,
故a3cosA+b3cosB=abc.
26.解:
过D作DE⊥AB于E,
设BC=2a,则AC=2a,AD=CD=a,
由勾股定理得:BD==a,
由勾股定理得:AB==2a,
∵∠A=∠B=45°,∠DEA=90°,
∴AE=DE=AD×cosA=×a=a,
∵在Rt△BED中,由勾股定理得:BE==a,
∴sin∠ABD===,
tan∠ABD===.
27.解:设AC=x,在Rt△ACP中∠PAC=45°,则∠P=45°,
所以PC=AC=x,
∵山顶A处高出水面50m,
∴BC=50,
∴BP′=BP=PC+BC=x+50,
∵∠P′AC=60°,
∴P′C=tan60°?AC=x,
∴BP′=P′C﹣BC=x﹣50,
∴x+50=x﹣50,
x=50(+1),
∴h=PB=50(+1)+50=50+100(m),
答:直升机离湖面的高度是50+100m.
解直角三角形》单元测试卷
一.选择题(共10小题)
1.△ABC的周长为36cm,∠C=90°,tanA=,则△ABC的面积是( )
A.30cm2
B.54cm2
C.60cm2
D.108cm2
2.若0°<α<45°,则下列各式中正确的是( )
A.sinα>cosα
B.cosα>sinα
C.cotα<1
D.tanα>cotα
3.若tanα=2,则的值为( )
A.
B.
C.
D.1
4.若α是直角三角形的一个锐角,且cosα=sin40°,则α的度数为( )
A.20°
B.30°
C.40°
D.50°
5.若2cosα﹣=0,则锐角α=( )
A.30°
B.15°
C.45°
D.60°
6.用计算器求sin20°+tan54°33′的结果等于(结果精确到0.01)( )
A.2.25
B.1.55
C.1.73
D.1.75
7.如图,∠α的顶点在坐标原点,始边与x轴的正半轴重合,终边上一点的横坐标是3,且tanα=,则OP=( )
A.3
B.4
C.
D.5
8.如图,C、D、B在同一直线上,∠ACB=30°,∠ADB=45°,CD=14,∠ABC=90°.那么AB=( )
A.
+7
B.
+7
C.﹣7
D.
+7
9.如图,从小明家到学校有两条路.一条沿北偏东45°方向可直达学校前门,另一条从小明家一直往东到商店处,再向正北走100米到学校后门.若两条路的路程相等,学校南北走向,则学校从前门到后门的距离是( )
A.100米
B.100米
C.100米
D.100米
10.如图所示,两建筑物的水平距离为s米,从A点测得D点的俯角为α,测得C点的俯角为β,则较低的建筑物的高为( )
A.s?tanβ米
B.s?tan(α﹣β)米
C.s(tanβ﹣tanα)米
D.米
二.填空题(共10小题)
11.如图,B、C是河岸边两点,A是对岸岸边一点,测得∠ABC=45°,∠ACB=45°,BC=60
m,则点A到对岸BC的距离是
m.
12.如图,△ABC的顶点都在方格纸的格点上,则cosA=
.
13.用“>”或“<”连结:
cos18°
cos18°3′;
tan31°
tan32°;
tan29°30′
cot60°29′;
sin39°
cos51°;
cot30°
sin89°;
sinα+cosα
1(α为锐角)
14.用计算器计算:sin35°≈
(结果保留两个有效数字).
15.周长为22的等腰三角形,一边长为8,则底角的余弦值为
.
16.某校数学兴趣小组在测量一座池塘边上A,B两点间的距离时用了以下三种测量方法,如图所示.图中a,b,c表示长度,β表示角度.请你求出AB的长度(用含有a,b,c,β字母的式子表示).
(1)AB=
;(2)AB=
;(3)AB=
.
17.在一坡比为1:7的斜坡上种有两棵小树,它们之间的距离AB为10米,则这两棵树的高度差BC为
米.
18.△ABC中,∠C=90°,cosA=,sinB=|n|﹣,则n=
.
19.在△ABC中,∠A,∠B都是锐角,且满足|sinA﹣|+(﹣cosB)2=0,则∠C的度数为
.
20.如图,某飞机于空中探测某座山的高度,在点A处飞机的飞行高度是AF=3700米,从飞机上观测山顶目标C的俯角是45°,飞机继续以相同的高度飞行300米到B地,此时观察目标C的俯角是50°,则这座山的高度CD是
米(参考数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.20)
三.解答题(共7小题)
21.计算:
(1)sin60°+
cos45°+sin30°?cos30°;
(2)3tan30°﹣+cos0°?cos45°;
(3)+;
(4)cos21°+cos22°+…+cos288°+cos289°.
22.△ABC中,∠BAC=90°,AD是高,BD=9,tanB=,求AD、AC、BC.
23.如图,河流的两岸MN、PQ互相平行,河岸PQ上有一排间隔为50m的电线杆C、D、E….某人在河岸MN的A处测得∠DAN=38°,然后沿河岸走了120m到达B处,测得∠CBN=70°.求河流的宽度CF.(结果精确到0.1m,参考数据:sin38°≈0.62,cos38°≈0.79,tan38°≈0.78,sin70°≈0.94,cos70°≈0.34,tan70°≈2.75)
24.如图,新华都超市的自动扶梯AB段的长度为20米,倾斜角为9°,求扶梯的高度BC为多少米?(精确到0.1米)
25.在Rt△ABC中,∠C=90°,求证:a3cosA+b3cosB=abc.
26.已知△ABC中,∠C=90°,∠A=45°,BD为AC边上中线,求sin∠ABD和tan∠ABD的值.
27.如图,在湖边高出水面50m的山顶A处,望见一架直升机停留在湖面上空某处,观察到直升机底部标志P处的仰角为45°,又观察其在湖中之像P′的俯角为60°,试求直升机离湖面的高度h(观察时湖面处于平静状态).
参考答案与试题解析
一.选择题(共10小题)
1.解:∵tanA==,
∴设AC=3x,则BC=4x,
根据勾股定理可以得到:AB=5x,
则3x+4x+5x=36,
解得:x=3,
则AC=9cm,BC=12cm,AB=15cm.
则△ABC的面积是:
AC?BC=×9×12=54cm2.
故选:B.
2.解:∵0°<α<45°,
∴sinα<sin(90°﹣α)=cosα,
∵tan45°=cot45°=1,
∴cotα>1,tanα<1,
∴cotα>tanα.
故选:B.
3.解:因为tanα==2,
∴原式====.
故选:C.
4.解:∵cosα=sin40°,
∴α=90°﹣40°=50°.
故选:D.
5.解:∵2cosα﹣=0,
∴cosα=,
∴α=30°.
故选:A.
6.解:sin20°+tan54°33′
=sin20°+tan54.55°
=0.3420+1.4045
=1.7465
≈1.75.
故选:D.
7.解:∵tanα==,
∴P点的纵坐标为3tanα=3×=4.
OP的长为.
故选:D.
8.解:在Rt△ABD中,tan∠ADB=,故AB=BD.
在Rt△ACB中,tan∠ACB=,
解得AB=7.
故选:D.
9.解:如图,由题意得∠DAB=45°,BC=100,AB+100=AD,
∵cos∠DAB==,
∴AB=AD=(AB+100),
解得:AB=100+100,
∴BD=AB=100+100,
∴CD=100(米).
故选:A.
10.解:作AE∥BC,与CD延长线相交于E点.
由于两建筑物的水平距离为s米,从A点测得D点的俯角为α,测得C点的俯角为β,
在Rt△ACE中,CE=tanβ?s;
在Rt△ADE中,DE=tanα?s,
则CD=s(tanβ﹣tanα).
故选:C.
二.填空题(共10小题)
11.解:由题意可得:∠A=180°﹣45°﹣45°=90°,
AB=AC=BC×sin45°=30.
∵面积S=AB×AC=BC×h,
∴h=30.
故点A到对岸BC的距离是30米.
12.解:
从图形可知:AE=4,CE=2,
由勾股定理得:AC=,
cosA===,
故答案为:.
13.解:cos18°>cos18°3′;
tan31°<tan32°;
tan29°30′<cot60°29′(cot60°29′=tan29°31′);
sin39°=cos51°(cos51°=sin39°);
cot30°>sin89°(cot30°>cot45°=1);
sinα+cosα>1(α为锐角).
故答案为>、<、<、=、>、>.
14.解:sin35°≈0.5736≈0.57.
故答案为:0.57.
15.解:作AD⊥BC于D,
当腰长AB=8时,底边长BC=6,
则BD=BC=3,
cosB==;
当底边长BC=8时,腰长AB=7,
则BD=BC=4,
cosB==,
故答案为:或.
16.解:(1)在直角△ABC中,AB=;
(2)在直角△ABC中,AB=a?tanβ;
(3)△ABC∽△EDC,
∴=,求得AB=.
故答案为:、a?tanβ、.
17.解:由题意,BC:AC=1:7,
在Rt△ABC中,AB=10m,
设BC=xm,则AC=7xm,
∴x2+49x2=100,
解得,x=(m),
∴BC=m.
故答案为:.
18.解:在△ABC中,∠C=90°,
∴∠A+∠B=90°,
∴sinB=cosA,
∴|n|﹣=,
∴|n|=1,
∴n=±1.
故答案为±1.
19.解:∵|sinA﹣|+(﹣cosB)2=0,
∴sinA=,cosB=.
∴∠A=45°,∠B=30°.
由三角形的内角和是180°可知∠C=180°﹣30°﹣45°=105°.
故答案为:105°.
20.解:设EC=x,
在Rt△BCE中,tan∠EBC=,
则BE==x,
在Rt△ACE中,tan∠EAC=,
则AE==x,
∵AB+BE=AE,
∴300+x=x,
解得:x=1800,
这座山的高度CD=DE﹣EC=3700﹣1800=1900(米).
故答案为:1900.
三.解答题(共7小题)
21.(1)sin60°+
cos45°+sin30°?cos30°;
=×+×+×,
=+
(2)3tan30°﹣+cos0°?cos45°;
=3×﹣(﹣1)+1×,
=﹣+1+,
=1+,
(3)+;
=+,
=1﹣﹣,
=﹣﹣,
(4)cos21°+cos22°+…+cos288°+cos289°.
=(cos21°+cos289°)+(cos22°+cos288°)+…cos245°,
=(cos21°+sin21°)+(cos22°+sin22°)+…cos245°,
=1+1+…+,
=44.
22.解:如图所示:∵∠ADB=90°,tanB=,BD=9,
∴tanB===,
解得:AD=12,
故AB==15,
tanB===,
解得:AC=20,
故BC==25.
23.解:过点C作CG∥DA交AB于点G.
∵MN∥PQ,CG∥DA,
∴四边形AGCD是平行四边形.
∴AG=CD=50m,∠CGB=38°.
∴GB=AB﹣AG=120﹣50=70(m).
∴tan38°==0.78,
在Rt△BFC中,
tan70°==2.75,
∴BF=,
∴==0.78,
解得:CF≈76.2(m).
答:河流的宽是76.2米.
24.解:由题意,在Rt△ABC中,
∠A=9°,有三角函数关系可知,
BC=AB?sinα=3.1米
即扶梯的高度约为3.1米.
25.证明:如图,cosA=,cosB=,
由勾股定理得,a2+b2=c2,
所以a3?+b3?=(a2+b2)=?c2=abc,
故a3cosA+b3cosB=abc.
26.解:
过D作DE⊥AB于E,
设BC=2a,则AC=2a,AD=CD=a,
由勾股定理得:BD==a,
由勾股定理得:AB==2a,
∵∠A=∠B=45°,∠DEA=90°,
∴AE=DE=AD×cosA=×a=a,
∵在Rt△BED中,由勾股定理得:BE==a,
∴sin∠ABD===,
tan∠ABD===.
27.解:设AC=x,在Rt△ACP中∠PAC=45°,则∠P=45°,
所以PC=AC=x,
∵山顶A处高出水面50m,
∴BC=50,
∴BP′=BP=PC+BC=x+50,
∵∠P′AC=60°,
∴P′C=tan60°?AC=x,
∴BP′=P′C﹣BC=x﹣50,
∴x+50=x﹣50,
x=50(+1),
∴h=PB=50(+1)+50=50+100(m),
答:直升机离湖面的高度是50+100m.
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
