12.3 等腰三角形说课课件(第一课时)
文档属性
| 名称 | 12.3 等腰三角形说课课件(第一课时) |

|
|
| 格式 | rar | ||
| 文件大小 | 813.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-10-22 00:00:00 | ||
图片预览








文档简介
(共26张PPT)
12.3 等腰三角形
(第一课时)
义务教育课程标准实验教科书 数学(八上)
教材
分析
教法
分析
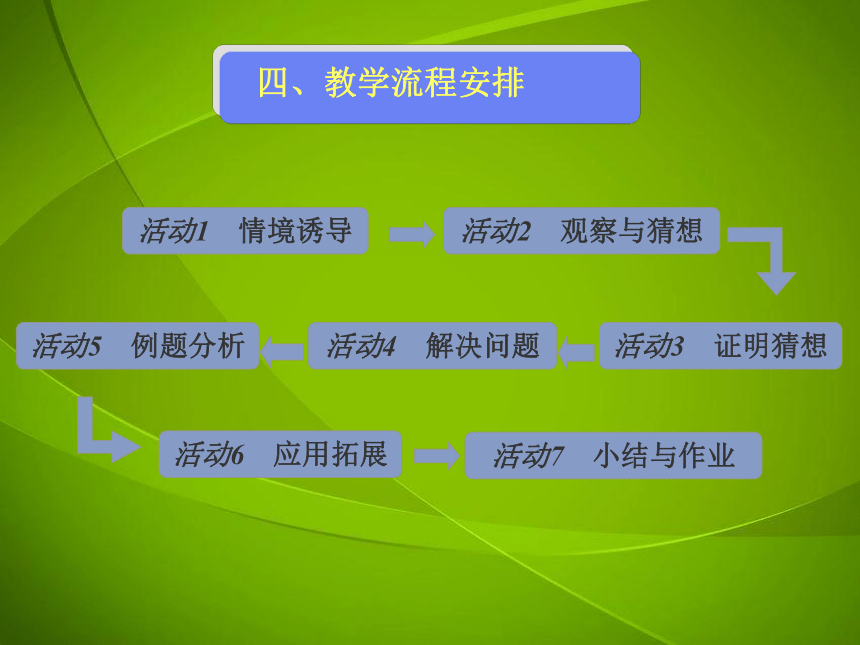
教学流程安排
学法分析
教学过程设计
设计简要说明
1、教材的地位和作用
本节课是人教版八年级上册12.3“等腰三角形”的第一课时,是学生在学习了轴对称图形的基础上又要学习的一种特殊且重要的轴对称图形。
等腰三角形的性质(1、两个底角相等;2、三线合一)对学生今后的学习具有很大的用处,特别是性质1又称为“等边对等角”,是学生今后证明两角相等的常用依据之一,性质2是学生今后证明线段相等、两角相等及两直线垂直的重要依据。
因此本节课起着承上启下的作用,也是中考的热点之一。
一、教 材 分 析
⑴知识目标:①、掌握等腰三角形的性质。
②、运用等腰三角形的性质进行证明和计算。
⑵能力目标:培养学生动手操作能力、逻辑推理能力、数形结合能力、运用数学能力,并在应用的过程培养学生列方程思想以及分类讨论的思想。
⑶情感目标:让学生体会数学来源于生活,数学服务于生活,以及培养学生的集体荣誉感和团结合作、勇于创新的精神。
2、教学目标
一、教 材 分 析
重点:等腰三角形的性质及应用
难点:1、等腰三角形性质的证明
2、实际问题抽象为数学模型
3、教学重点、难点
一、教 材 分 析
二、教 法 分 析
荷兰著名数学教育家弗赖登塔尔指出:“数学的整体结构应该存在于现实中,只有密切联系现实,教的数学才能充满各种关系,学生才能将所学的数学与现实结合,并且能够运用”。本节课先引出生活实际问题,创设情境,引入课题,再让学生通过折纸猜想、验证等腰三角形的性质,然后运用全等三角形的判定和性质加以论证,最后实际问题得到解决并拓展。在整个教学过程中,突出学生的探究过程,四个同学为一小组,将全班分为十二个小组,每三个小组为一个单位,引入竞争机制,设计了“活动评分表”,在每次活动中对小组合作情况做及时的评价,真正实现以学生为主体的教学宗旨。
三、学 法 分 析
课程改革的一个重要目标是学习方式的转变,强调让学生在“做数学”中“学数学”,最后能够“用数学”,本节课采用“动手操作、自主探究、小组合作”的学习方法,在整个学习过程中,贯穿着分组讨论,同学之间充满着互帮互助的合作精神,变“被动”为“主动”,变“要我学”为“我要学”,让学生真正成为课堂的主人。
活动1 情境诱导
四、教学流程安排
活动2 观察与猜想
活动3 证明猜想
活动6 应用拓展
活动5 例题分析
活动4 解决问题
活动7 小结与作业
情境1
如图,某工厂工人师傅发现的一个残缺不全的等腰三角形模具,顶角度数为40°,工人师傅问:那么其余两个角应分别为 度和 度?
400
五、教学过程设计
活动1 情境诱导①
情境2
将一把等腰三角尺和一个重锤如图放置,就能检查
一根横梁是否水平,你知道这是为什么吗?
活动1 情境诱导②
五、教学过程设计
在△ABC中,AB = AC。
A
B
C
腰
腰
底
顶角
底角
底角
复习概念
五、教学过程设计
活动2 观察与猜想
五、教学过程设计
猜想:
1、等腰三角形的两个底角相等.
2、等腰三角形的顶角平分线、底边上的中线 和底边上的高互相重合.
活动2 观察与猜想
五、教学过程设计
已知:△ABC中,AB=AC,求证:∠B= ∠C
(1)性质1(等腰三角形的两个底角相等)的条件和结论分别是什么?
(2)用数学符号如何表达条件和结论?
(3)如何证明?
(4)受性质1的证明的启发,你能证明性质2(等腰三角形的顶角平分线、 底边上的中线、底边上的高相互重合)吗?
(5)由“三线合一”引出证明性质1的其他方法。
D
A
B
C
A
B
C
D
方法一
A
C
D
B
方法二
方法三
活动3 证明猜想
五、教学过程设计
等腰三角形的两个底角相等.
简称 “在同一个三角形中,等边对等角”
等腰三角形的顶角平分线、底边上的中线 和底边上的高互相重合.
简称“等腰三角形三线合一”
五、教学过程设计
活动3 证明猜想
等腰三角形的性质1:
等腰三角形的性质2:
用数学符号语言描述等腰三角形性质2
在△ABC中, AB=AC 时,
(1) ∵AD⊥BC,∴∠_____ = ∠_____,____= ____.
(2) ∵AD是中线,∴____⊥____ ,∠_____ =∠_____.
(3) ∵AD是角平分线,∴____ ⊥____ ,_____ =_____.
A
B
C
D
BAD
CAD
CAD
BD
CD
AD
BC
BD
BAD
BC
AD
CD
活动3 证明猜想
五、教学过程设计
如右图,某工厂工人师傅发现的一个残缺不全的等腰三角形模具,顶角度数为40° ,工人师傅问:那么其余两个角应分别为 和 ?
40°
活动4 解决问题①
五、教学过程设计
将一把等腰三角尺和一个重锤如图放置,就能检查
一根横梁是否水平,你知道这是为什么吗?
活动4 解决问题②
五、教学过程设计
例题:如图,在△ABC中,AB=AC,点D在AC上,且BD=BC=AD,求△ABC各角的度数
A
D
B
C
活动5 例题分析
五、教学过程设计
方程思想
一、变式训练
①等腰三角形的一个角是40°,它的另外两个角是 ;
②等腰三角形的一个角是100°,它的另外两个角是 。
注意:在等腰三角形中,
① 0°<顶角<180°
② 0°<底角<90°
活动6 应用拓展①
五、教学过程设计
分类思想
二、例题改造
如图,GF⊥AF于点F,且AB=BC=CD
=DE=EF=FG,求∠A 的度数.
方程思想
五、教学过程设计
活动6 应用拓展②
1、这节课我们主要学习了什么内容?
2、有哪些收获?
必做题:教科书习题12.3第1、4、6题。
选做题:导学12.3第2、8、10题。
作业
活动7 小结与作业
五、教学过程设计
小结
本节课主要通过生活中的实际问题创造情境,提供可探究性的问题,激发学生的求知欲。在整个教学过程中,突出学生的探究过程;同时设计了“活动评分表”, 引入竞争机制,在每次活动中对小组合作情况作及时的评价,再次激发学生的学习兴趣,并且弘扬学生的团体合作精神,变“要我学”为“我要学”,最后以实际问题得到解决并拓展而结束,让学生体会到成功的喜悦。本节课主要设计程序为:“情境诱导—观察与猜想—证明猜想—解决问题—例题分析—应用拓展—小结及作业”。有效地进行从质疑到解疑,学以致用,在应用新知解决生活实际问题时,充分体现了数学源自生活,又服务于生活,教学过程还渗透分类讨论思想、列方程思想,有利于提高学生的数学修养。
六、教学设计简要说明
12.3等腰三角形(一)
一、复习等腰三角形的有关定义
二、等腰三角形的性质
性质1:等腰三角形的两个底角相等(简称“等边对等角”)
性质2:等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合(简称“三线合一”) 定理的证明:
性质1证明
性质2证明 应用新知,解决问题
小结 作业
活动评分表
1
2
3
4
附:板书设计
12.3 等腰三角形
(第一课时)
义务教育课程标准实验教科书 数学(八上)
教材
分析
教法
分析
教学流程安排
学法分析
教学过程设计
设计简要说明
1、教材的地位和作用
本节课是人教版八年级上册12.3“等腰三角形”的第一课时,是学生在学习了轴对称图形的基础上又要学习的一种特殊且重要的轴对称图形。
等腰三角形的性质(1、两个底角相等;2、三线合一)对学生今后的学习具有很大的用处,特别是性质1又称为“等边对等角”,是学生今后证明两角相等的常用依据之一,性质2是学生今后证明线段相等、两角相等及两直线垂直的重要依据。
因此本节课起着承上启下的作用,也是中考的热点之一。
一、教 材 分 析
⑴知识目标:①、掌握等腰三角形的性质。
②、运用等腰三角形的性质进行证明和计算。
⑵能力目标:培养学生动手操作能力、逻辑推理能力、数形结合能力、运用数学能力,并在应用的过程培养学生列方程思想以及分类讨论的思想。
⑶情感目标:让学生体会数学来源于生活,数学服务于生活,以及培养学生的集体荣誉感和团结合作、勇于创新的精神。
2、教学目标
一、教 材 分 析
重点:等腰三角形的性质及应用
难点:1、等腰三角形性质的证明
2、实际问题抽象为数学模型
3、教学重点、难点
一、教 材 分 析
二、教 法 分 析
荷兰著名数学教育家弗赖登塔尔指出:“数学的整体结构应该存在于现实中,只有密切联系现实,教的数学才能充满各种关系,学生才能将所学的数学与现实结合,并且能够运用”。本节课先引出生活实际问题,创设情境,引入课题,再让学生通过折纸猜想、验证等腰三角形的性质,然后运用全等三角形的判定和性质加以论证,最后实际问题得到解决并拓展。在整个教学过程中,突出学生的探究过程,四个同学为一小组,将全班分为十二个小组,每三个小组为一个单位,引入竞争机制,设计了“活动评分表”,在每次活动中对小组合作情况做及时的评价,真正实现以学生为主体的教学宗旨。
三、学 法 分 析
课程改革的一个重要目标是学习方式的转变,强调让学生在“做数学”中“学数学”,最后能够“用数学”,本节课采用“动手操作、自主探究、小组合作”的学习方法,在整个学习过程中,贯穿着分组讨论,同学之间充满着互帮互助的合作精神,变“被动”为“主动”,变“要我学”为“我要学”,让学生真正成为课堂的主人。
活动1 情境诱导
四、教学流程安排
活动2 观察与猜想
活动3 证明猜想
活动6 应用拓展
活动5 例题分析
活动4 解决问题
活动7 小结与作业
情境1
如图,某工厂工人师傅发现的一个残缺不全的等腰三角形模具,顶角度数为40°,工人师傅问:那么其余两个角应分别为 度和 度?
400
五、教学过程设计
活动1 情境诱导①
情境2
将一把等腰三角尺和一个重锤如图放置,就能检查
一根横梁是否水平,你知道这是为什么吗?
活动1 情境诱导②
五、教学过程设计
在△ABC中,AB = AC。
A
B
C
腰
腰
底
顶角
底角
底角
复习概念
五、教学过程设计
活动2 观察与猜想
五、教学过程设计
猜想:
1、等腰三角形的两个底角相等.
2、等腰三角形的顶角平分线、底边上的中线 和底边上的高互相重合.
活动2 观察与猜想
五、教学过程设计
已知:△ABC中,AB=AC,求证:∠B= ∠C
(1)性质1(等腰三角形的两个底角相等)的条件和结论分别是什么?
(2)用数学符号如何表达条件和结论?
(3)如何证明?
(4)受性质1的证明的启发,你能证明性质2(等腰三角形的顶角平分线、 底边上的中线、底边上的高相互重合)吗?
(5)由“三线合一”引出证明性质1的其他方法。
D
A
B
C
A
B
C
D
方法一
A
C
D
B
方法二
方法三
活动3 证明猜想
五、教学过程设计
等腰三角形的两个底角相等.
简称 “在同一个三角形中,等边对等角”
等腰三角形的顶角平分线、底边上的中线 和底边上的高互相重合.
简称“等腰三角形三线合一”
五、教学过程设计
活动3 证明猜想
等腰三角形的性质1:
等腰三角形的性质2:
用数学符号语言描述等腰三角形性质2
在△ABC中, AB=AC 时,
(1) ∵AD⊥BC,∴∠_____ = ∠_____,____= ____.
(2) ∵AD是中线,∴____⊥____ ,∠_____ =∠_____.
(3) ∵AD是角平分线,∴____ ⊥____ ,_____ =_____.
A
B
C
D
BAD
CAD
CAD
BD
CD
AD
BC
BD
BAD
BC
AD
CD
活动3 证明猜想
五、教学过程设计
如右图,某工厂工人师傅发现的一个残缺不全的等腰三角形模具,顶角度数为40° ,工人师傅问:那么其余两个角应分别为 和 ?
40°
活动4 解决问题①
五、教学过程设计
将一把等腰三角尺和一个重锤如图放置,就能检查
一根横梁是否水平,你知道这是为什么吗?
活动4 解决问题②
五、教学过程设计
例题:如图,在△ABC中,AB=AC,点D在AC上,且BD=BC=AD,求△ABC各角的度数
A
D
B
C
活动5 例题分析
五、教学过程设计
方程思想
一、变式训练
①等腰三角形的一个角是40°,它的另外两个角是 ;
②等腰三角形的一个角是100°,它的另外两个角是 。
注意:在等腰三角形中,
① 0°<顶角<180°
② 0°<底角<90°
活动6 应用拓展①
五、教学过程设计
分类思想
二、例题改造
如图,GF⊥AF于点F,且AB=BC=CD
=DE=EF=FG,求∠A 的度数.
方程思想
五、教学过程设计
活动6 应用拓展②
1、这节课我们主要学习了什么内容?
2、有哪些收获?
必做题:教科书习题12.3第1、4、6题。
选做题:导学12.3第2、8、10题。
作业
活动7 小结与作业
五、教学过程设计
小结
本节课主要通过生活中的实际问题创造情境,提供可探究性的问题,激发学生的求知欲。在整个教学过程中,突出学生的探究过程;同时设计了“活动评分表”, 引入竞争机制,在每次活动中对小组合作情况作及时的评价,再次激发学生的学习兴趣,并且弘扬学生的团体合作精神,变“要我学”为“我要学”,最后以实际问题得到解决并拓展而结束,让学生体会到成功的喜悦。本节课主要设计程序为:“情境诱导—观察与猜想—证明猜想—解决问题—例题分析—应用拓展—小结及作业”。有效地进行从质疑到解疑,学以致用,在应用新知解决生活实际问题时,充分体现了数学源自生活,又服务于生活,教学过程还渗透分类讨论思想、列方程思想,有利于提高学生的数学修养。
六、教学设计简要说明
12.3等腰三角形(一)
一、复习等腰三角形的有关定义
二、等腰三角形的性质
性质1:等腰三角形的两个底角相等(简称“等边对等角”)
性质2:等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合(简称“三线合一”) 定理的证明:
性质1证明
性质2证明 应用新知,解决问题
小结 作业
活动评分表
1
2
3
4
附:板书设计
