华东师大版九年级数学上册第24章解直角三角形检测题(word版含解析)
文档属性
| 名称 | 华东师大版九年级数学上册第24章解直角三角形检测题(word版含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-12 00:00:00 | ||
图片预览



文档简介
第24章
解直角三角形检测题
(本检测题满分:120分,时间:120分钟)
一、选择题(每小题2分,共24分)
1.计算:
A.
B.
C.
D.
2.在直角三角形中,已知,,,则=(
)
A.
B.
C.
D.
3.(2013·浙江温州中考)如图,在中,则的值是(
)
A.
B.
C.
D.
4.如图,四边形ABCD是梯形,AD∥BC,CA是∠BCD的平分线,且AB⊥AC,AB=4,AD=6,则tan
B=(
)
A.2
B.2
C.
D.
5.如图,Rt△ABC中,90°,将△ABC折叠,使A点与BC的中点D重合,折痕为MN,则线段BN的长为(
)
A.
B.
C.4
D.5
6.在△ABC中,若三边BC,CA,AB满足
BC∶CA∶AB=5∶12∶13,则cos
B=(
)
A.
B.
C.
D.
7.已知,,点,点F分别在射线AD,射线BC上,若点与点关于对称,点与点关于对称,与相交于点,则(
)
A.
B.
C.
D.
第7题图
8.河堤横断面如图所示,堤高BC=6
m,迎水坡AB的坡比为1∶,则AB的长为(
)
A.12
m
B.4
m
C.5
m
D.6
m
9.如图,一个小球由地面沿着坡度的坡面向上前进了10
m,此时小球距离地面的高度为(
)
A.5
m
B.2
m
C.4
m
D.
m
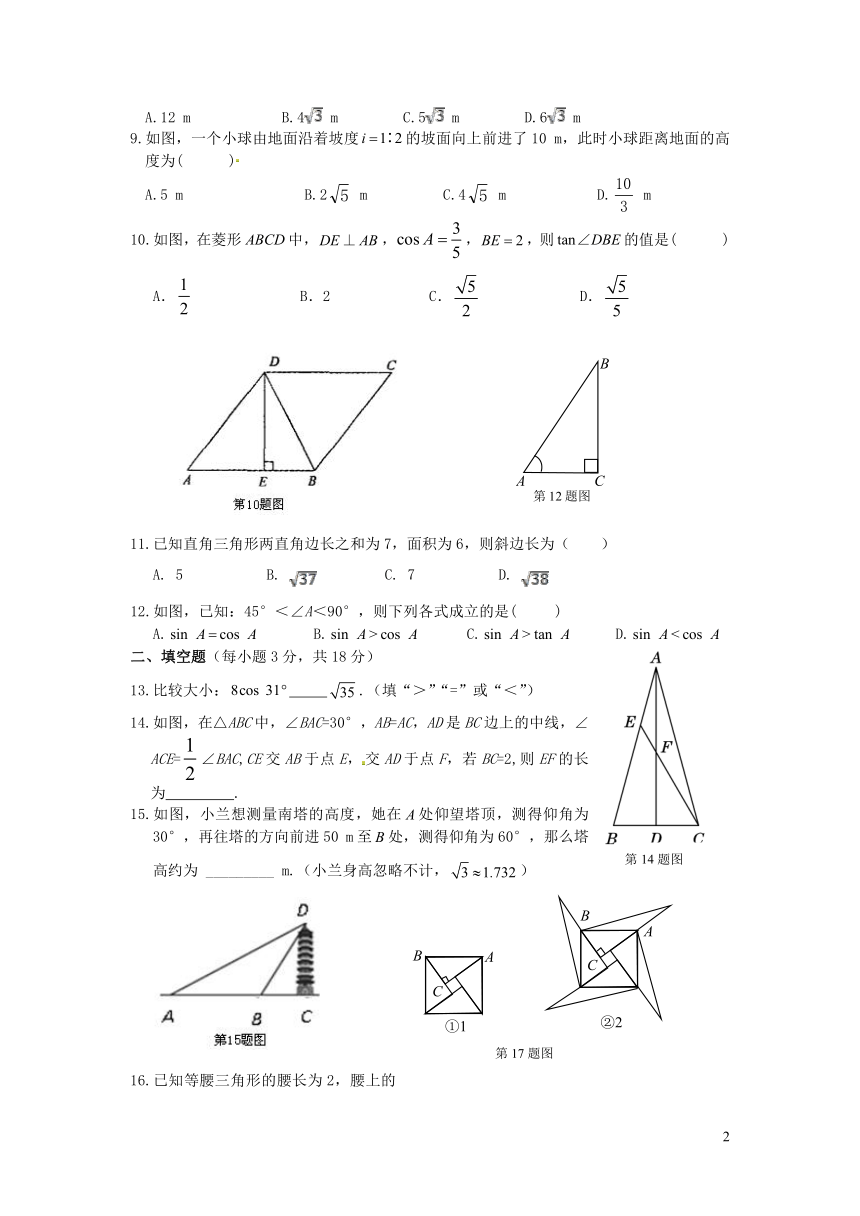
10.如图,在菱形中,,,,则的值是(
)
A.
B.2
C.
D.
11.已知直角三角形两直角边长之和为7,面积为6,则斜边长为(
)
A.
5
B.
C.
7
D.
12.如图,已知:45°<∠A<90°,则下列各式成立的是(
)
A.
B.
C.
D.
二、填空题(每小题3分,共18分)
13.比较大小:
.(填“>”“=”或“<”)
14.如图,在△ABC中,∠BAC=30°,AB=AC,AD是BC边上的中线,∠ACE=∠BAC,CE交AB于点E,交AD于点F,若BC=2,则EF的长为
.
15.如图,小兰想测量南塔的高度,她在处仰望塔顶,测得仰角为30°,再往塔的方向前进50
m至处,测得仰角为60°,那么塔高约为
_________
m.(小兰身高忽略不计,)
16.已知等腰三角形的腰长为2,腰上的高为1,则它的底角等于________
.
17.图①是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的,若,将四个直角三角形中边长为6的直角边分别向外延长一倍,得到图②所示的“数学风车”,则这个风车的外围周长是__________.
18.在△ABC中,∠90°,AB=2BC,现给出下列结论:
①sin
A=;②cos
B=;③tan
A=;④tan
B=,
其中正确的结论是
.(只需填上正确结论的序号)
三、解答题(共78分)
19.(8分)计算下列各题:
(1);(2).
20.(8分)如图,在Rt△ABC中,∠C=90°,AB=10,sin
A=,求BC的长和tan
B的值.
第20题图
第21题图
21.(10分)如图,在一笔直的海岸线l上有A,B两个观测站,A在B的正东方向,AB=2(单位:km).有一艘小船在点P处,从A测得小船在北偏西60°的方向,从B测得小船在北偏东45°的方向.
(1)求点P到海岸线l的距离;
(2)小船从点P处沿射线AP的方向航行一段时间后,到达点C处,此时,从B测得小船在北偏西15°的方向.求点C与点B之间的距离.(上述2小题的结果都保留根号)
22.(10分)如图,为了测量某建筑物CD的高度,先在地面上用测角仪自A处测得建筑物顶部的仰角是30°,然后在水平地面上向建筑物前进了100
m,此时自B处测得建筑物顶部的仰角是45°.已知测角仪的高度是1.5
m,请你计算出该建筑物的高度.(取
≈1.732,结果精确到1
m)
23.(8分)如图,在梯形中,,,.
(1)求的值;(2)若长度为,求梯形的面积.
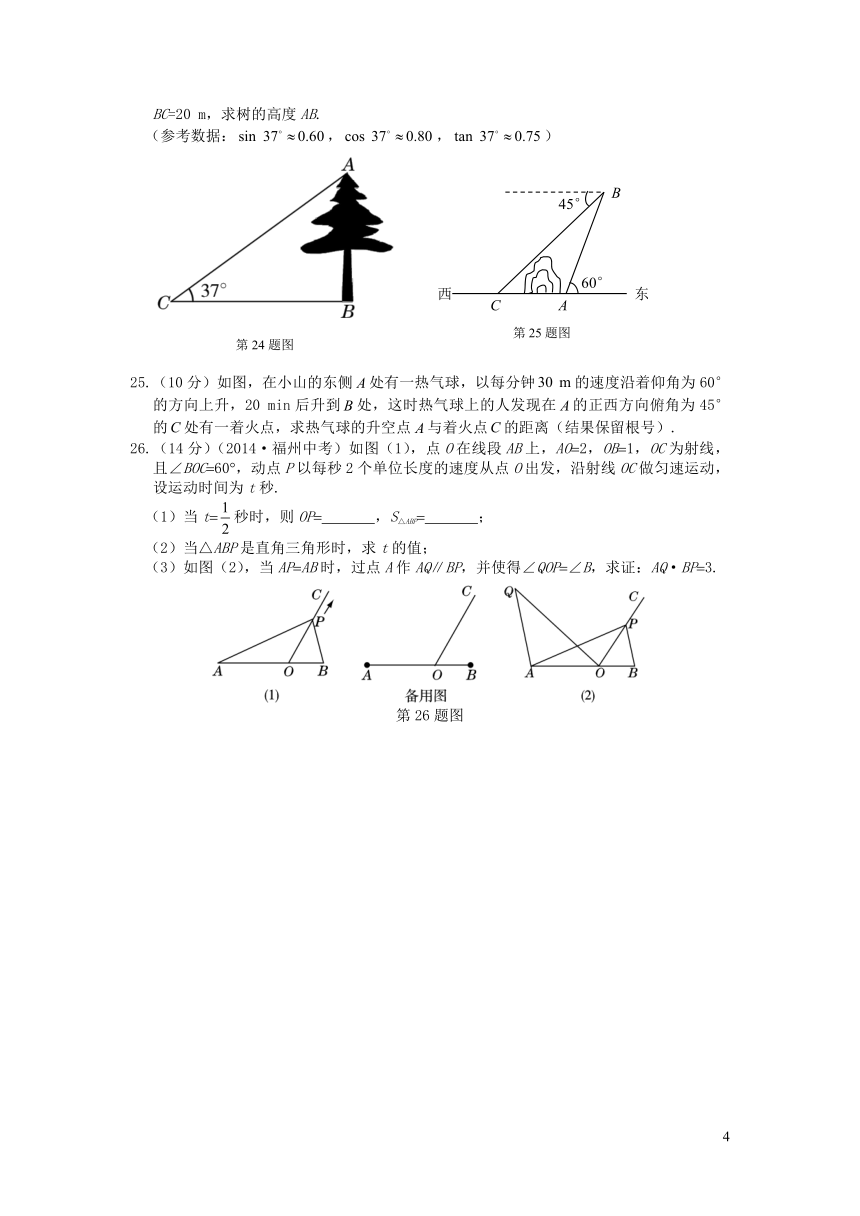
24.(10分)如图,在一次数学课外实践活动中,小文在点C处测得树的顶端A的仰角为37°,BC=20
m,求树的高度AB.
(参考数据:,,)
25.(10分)如图,在小山的东侧处有一热气球,以每分钟的速度沿着仰角为60°的方向上升,20
min后升到处,这时热气球上的人发现在的正西方向俯角为45°的处有一着火点,求热气球的升空点与着火点的距离(结果保留根号).
26.(14分)(2014·福州中考)如图(1),点O在线段AB上,AO2,OB1,OC为射线,且∠BOC60,动点P以每秒2个单位长度的速度从点O出发,沿射线OC做匀速运动,设运动时间为t秒.
(1)当t秒时,则OP
,S△ABP
;
(2)当△ABP是直角三角形时,求t的值;
(3)如图(2),当APAB时,过点A作AQ∥BP,并使得∠QOP∠B,求证:AQ·BP3.
第26题图
第24章
解直角三角形检测题参考答案
1.C
解析:
2.D
解析:在中,∵
,,∴
,
∴
,∴
.
3.C
解析:.
4.B
解析:如图,过点D作DE∥AB交BC于点E,则四边形ABED是平行四边形,
∴
BE=AD=6.
∵
AB⊥AC,∴
DE⊥AC.∵
CA是∠BCD的平分线,∴
CD=CE.
∵
AD∥BC,∴
∠ACB=∠DAC=∠DCA.∴
CD=AD=6.
∴
BC=BE+CE=BE+CD=6+6=12.
∴
AC===8.∴
tan
B===2.
5.C
解析:设BN的长为x,则AN=9x,由题意得DN=AN=9x.因为D为BC的中点,所以.在Rt△BND中,∠B=90°,由勾股定理得,即,解得.
6.C
解析:设,则,,所以,
所以△是直角三角形,且∠.
所以在△ABC中,.
7.A
解析:设.由题意知,,∴
.
在中,,又,
∴
.
根据条件还可以得出,,.
A.在中,,
∴
,故选项A正确.
B.,故选项B错误.
C.,故选项C错误.
D.∵
,∴
,故选项D错误.
8.A
解析:先由坡比的定义,得BC∶AC=1∶.由BC=6
m,可得AC=6
m.
在Rt△ABC中,由勾股定理,得AB==12(m).
9.B
解析:设小球距离地面的高度为则小球水平移动的距离为
所以解得
10.B
解析:设
又因为在菱形中,所以所以
所以由勾股定理知所以2
11.A
解析:设直角三角形的两直角边长分别为则
所以斜边长
12.B
解析:在锐角三角函数中仅当∠45°时,,所以选项错误;
因为45°<∠A<90°,所以∠B<45°,即∠A>∠B,所以BC>AC,所以>,即,所以选项正确,选项错误;
>1,<1,所以选项错误.
13.>
解析:因为,所以∠.
14.
解析:过F点作FG∥BC交AB于点G.
∵
在△ABC中,AB=AC,AD是BC边上的中线,
∴
BD=CD=BC=1,∠BAD=∠CAD=∠BAC=15°,AD⊥BC.
∵
∠ACE=∠BAC,
∴
∠CAD=∠ACE=15°,
∴
AF=CF.
∵
∠ACD=(180°-30°)÷2=75°,
∴
∠DCE=75°-15°=60°.
在Rt△CDF中,
CF=
=2,DF=CD·tan
60°=.
又AF=CF,∴
AF=2.
∵
FG∥BC,
∴
GF∶BD=AF∶AD,即GF∶1=2∶(2+),
解得GF=4-2,
∴
EF∶EC=GF∶BC,即EF∶(EF+2)=(4-2)∶2,
解得EF=-1.
15.43.3
解析:因为,所以
所以所以.
16.15°或75°
解析:如图,.
在图①中,,所以∠∠;
在图②中,,所以∠∠.
17.76
解析:如图,因为,所以CD=12,
由勾股定理得所以这个风车的外围周长为
18.②③④
解析:因为∠C=90°,AB=2BC,所以∠A=30°,∠B=60°,所以②③④正确.
19.解:(1)
(2).
20.分析:由sin
A==求出BC的长,根据勾股定理求出AC的长,利用tan
B=求出tan
B的值.
解:∵
sin
A==,AB=10,∴
BC=4.
又∵
AC==2,∴
tan
B==.
21.分析:(1)如图,过点P作PD⊥AB于点D,设PD=
km,根据AD+BD=2列方程求解.
(2)过点B作BF⊥CA于点F,在Rt△ABF和Rt△BFC中解直角三角形求解.
解:(1)如图,过点P作PD⊥AB于点D,
设PD=
km,由题意可知∠PBD=45°,∠PAD=30°,
∴
在Rt△BDP中,BD=PD=
km,在Rt△PDA中,AD=PD=
km.
∵
AB=2
km,∴
=2.∴
==1.
∴
点P到海岸线l的距离为()km.
(2)如图,过点B作BF⊥CA于点F.
在Rt△ABF中,BF=AB·sin
30°=2×=1(km).
在△ABC中,∠C=180°∠BAC∠ABC=45°.
在Rt△BFC中,BC=BF=×1=(km).
∴
点C与点B之间的距离为
km.
点拨:此题是解直角三角形在现实生活中的应用,通过构造直角三角形求解.当利用勾股定理或锐角三角函数不能直接求解时,常采用作垂线、引入未知数(一般为待定的数)构造方程求解.
22.解:设,则由题意可知,m.
在Rt△AEC中,tan∠CAE=,即tan
30°=,
∴,即3x(x+100),解得x50+50.
经检验50+50是原方程的解.
∴
故该建筑物的高度约为
23.解:(1)∵
,∴
∠∠.
∵
∥,∴
∠∠∠.
在梯形中,∵
,∴
∠∠∠∠
∵
,∴
3∠
,
∴
∠30°
,∴
(2)如图,过点作于点.
在Rt△中,?
∠,
?
∠,∴
在Rt△中,,
∴
梯形的面积为
24.分析:利用解直角三角形求线段长,首先根据锐角三角函数的定义选取恰当的三角函数关系式,然后把已知的数据代入计算.本题根据锐角三角函数的定义得tan
37°=,把,BC=20
m代入tan
37°=中求出树的高度AB.
解:因为tan
37°=≈0.75,BC=20
m,所以AB≈0.75×20=15(m).
25.解:过点作于点..
因为∠,300
m,
所以300(-1)即热气球的升空点与着火点的距离为300(-1)
26.(1)解:1,;
(2)解:①∵
∠A<∠BOC60,∴
∠A不可能是直角.
②当∠ABP90时,如图所示(第26题答图(1)),
∵
∠BOC60,∴
∠OPB30.
∴
OP2OB,即2t2.∴
t1.
第26题答图(1)
③当∠APB90时,如图所示(第26题答图(2)),作PD⊥AB,垂足为D,则∠ADP∠PDB90.
在Rt△POD中,∵
∠POD=60,∴
∠OPD=30.
∵
OP2t,
∴
ODt,PDt,AD2t,BD1t(△BOP是锐角三角形).
第26题答图(2)
方法一:BP2BD2+PD2=(1t)23t2,AP2AD2+PD2=(2t)23t2.
∵
BP2AP2AB2,∴
(1t)23t2(2t)23t29,即4t2t20.
解得t1,t2(舍去).
方法二:∵
∠APD∠BPD90,∠B∠BPD90,
∴
∠APD∠B.∴
△APD∽△PBD.
∴
∴
PD2AD·BD.
于是(t)2(2t)(1t),即4t2t20.
解得t1,t2(舍去).
综上,当△ABP为直角三角形时,t1或.
(3)证法一:∵
APAB,∴
∠APB∠B.
如图所示(第26题答图(3)),作OE∥AP,交BP于点E,
∴
∠OEB∠APB∠B.
∵
AQ∥BP,∴
∠QAB∠B180.
又∵
∠3∠OEB180,∴
∠3∠QAB.
又∵
∠AOC∠2∠B∠1∠QOP,∠B∠QOP,
∴
∠1∠2.
在△QAO和△OEP中,∵
∠3∠QAO,∠1∠2,
∴
△QAO∽△OEP.
∴
,即AQ·EPEO·AO.
∵
OE∥AP,∴
△OBE∽△ABP.
∴
.∴
OEAP1,BPEP.
∴
AQ·BPAQ·EP
AQ·EPAO·EO213.
第26题答图(3)
证法二:如图所示(第26题答图(4)),连接PQ,设AP与OQ相交于点F.
∵
AQ∥BP,∴
∠QAP∠APB.
∵
APAB,∴
∠APB∠B.∴
∠QAP∠B.
又∵
∠QOP∠B,∴
∠QAP∠QOP.
在△QFA和△PFO中,∵
∠QAF∠FOP,∠QFA∠PFO,
∴
△QFA∽△PFO.∴
,即.
又∵
∠PFQ∠OFA,∴
△PFQ∽△OFA.∴
∠3∠1.
∵
∠AOC∠2∠B∠1∠QOP,∠B∠QOP,
∴
∠1∠2.∴
∠2∠3.
∴
△APQ∽△BPO.∴
.∴
AQ·BPAP·BO313.
第26题答图(4)
第3题图
第5题图
第8题图
第9题图
A
B
C
第12题图
①1
A
B
C
②2
A
B
C
第17题图
第14题图
B
C
A
东
西
45°
60°
第25题图
第24题图
第4题答图
第14题答图
第16题答图
B
C
D
②
A
A
B
C
D
①
A
B
C
D
第17题答图
第21题答图
4
解直角三角形检测题
(本检测题满分:120分,时间:120分钟)
一、选择题(每小题2分,共24分)
1.计算:
A.
B.
C.
D.
2.在直角三角形中,已知,,,则=(
)
A.
B.
C.
D.
3.(2013·浙江温州中考)如图,在中,则的值是(
)
A.
B.
C.
D.
4.如图,四边形ABCD是梯形,AD∥BC,CA是∠BCD的平分线,且AB⊥AC,AB=4,AD=6,则tan
B=(
)
A.2
B.2
C.
D.
5.如图,Rt△ABC中,90°,将△ABC折叠,使A点与BC的中点D重合,折痕为MN,则线段BN的长为(
)
A.
B.
C.4
D.5
6.在△ABC中,若三边BC,CA,AB满足
BC∶CA∶AB=5∶12∶13,则cos
B=(
)
A.
B.
C.
D.
7.已知,,点,点F分别在射线AD,射线BC上,若点与点关于对称,点与点关于对称,与相交于点,则(
)
A.
B.
C.
D.
第7题图
8.河堤横断面如图所示,堤高BC=6
m,迎水坡AB的坡比为1∶,则AB的长为(
)
A.12
m
B.4
m
C.5
m
D.6
m
9.如图,一个小球由地面沿着坡度的坡面向上前进了10
m,此时小球距离地面的高度为(
)
A.5
m
B.2
m
C.4
m
D.
m
10.如图,在菱形中,,,,则的值是(
)
A.
B.2
C.
D.
11.已知直角三角形两直角边长之和为7,面积为6,则斜边长为(
)
A.
5
B.
C.
7
D.
12.如图,已知:45°<∠A<90°,则下列各式成立的是(
)
A.
B.
C.
D.
二、填空题(每小题3分,共18分)
13.比较大小:
.(填“>”“=”或“<”)
14.如图,在△ABC中,∠BAC=30°,AB=AC,AD是BC边上的中线,∠ACE=∠BAC,CE交AB于点E,交AD于点F,若BC=2,则EF的长为
.
15.如图,小兰想测量南塔的高度,她在处仰望塔顶,测得仰角为30°,再往塔的方向前进50
m至处,测得仰角为60°,那么塔高约为
_________
m.(小兰身高忽略不计,)
16.已知等腰三角形的腰长为2,腰上的高为1,则它的底角等于________
.
17.图①是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的,若,将四个直角三角形中边长为6的直角边分别向外延长一倍,得到图②所示的“数学风车”,则这个风车的外围周长是__________.
18.在△ABC中,∠90°,AB=2BC,现给出下列结论:
①sin
A=;②cos
B=;③tan
A=;④tan
B=,
其中正确的结论是
.(只需填上正确结论的序号)
三、解答题(共78分)
19.(8分)计算下列各题:
(1);(2).
20.(8分)如图,在Rt△ABC中,∠C=90°,AB=10,sin
A=,求BC的长和tan
B的值.
第20题图
第21题图
21.(10分)如图,在一笔直的海岸线l上有A,B两个观测站,A在B的正东方向,AB=2(单位:km).有一艘小船在点P处,从A测得小船在北偏西60°的方向,从B测得小船在北偏东45°的方向.
(1)求点P到海岸线l的距离;
(2)小船从点P处沿射线AP的方向航行一段时间后,到达点C处,此时,从B测得小船在北偏西15°的方向.求点C与点B之间的距离.(上述2小题的结果都保留根号)
22.(10分)如图,为了测量某建筑物CD的高度,先在地面上用测角仪自A处测得建筑物顶部的仰角是30°,然后在水平地面上向建筑物前进了100
m,此时自B处测得建筑物顶部的仰角是45°.已知测角仪的高度是1.5
m,请你计算出该建筑物的高度.(取
≈1.732,结果精确到1
m)
23.(8分)如图,在梯形中,,,.
(1)求的值;(2)若长度为,求梯形的面积.
24.(10分)如图,在一次数学课外实践活动中,小文在点C处测得树的顶端A的仰角为37°,BC=20
m,求树的高度AB.
(参考数据:,,)
25.(10分)如图,在小山的东侧处有一热气球,以每分钟的速度沿着仰角为60°的方向上升,20
min后升到处,这时热气球上的人发现在的正西方向俯角为45°的处有一着火点,求热气球的升空点与着火点的距离(结果保留根号).
26.(14分)(2014·福州中考)如图(1),点O在线段AB上,AO2,OB1,OC为射线,且∠BOC60,动点P以每秒2个单位长度的速度从点O出发,沿射线OC做匀速运动,设运动时间为t秒.
(1)当t秒时,则OP
,S△ABP
;
(2)当△ABP是直角三角形时,求t的值;
(3)如图(2),当APAB时,过点A作AQ∥BP,并使得∠QOP∠B,求证:AQ·BP3.
第26题图
第24章
解直角三角形检测题参考答案
1.C
解析:
2.D
解析:在中,∵
,,∴
,
∴
,∴
.
3.C
解析:.
4.B
解析:如图,过点D作DE∥AB交BC于点E,则四边形ABED是平行四边形,
∴
BE=AD=6.
∵
AB⊥AC,∴
DE⊥AC.∵
CA是∠BCD的平分线,∴
CD=CE.
∵
AD∥BC,∴
∠ACB=∠DAC=∠DCA.∴
CD=AD=6.
∴
BC=BE+CE=BE+CD=6+6=12.
∴
AC===8.∴
tan
B===2.
5.C
解析:设BN的长为x,则AN=9x,由题意得DN=AN=9x.因为D为BC的中点,所以.在Rt△BND中,∠B=90°,由勾股定理得,即,解得.
6.C
解析:设,则,,所以,
所以△是直角三角形,且∠.
所以在△ABC中,.
7.A
解析:设.由题意知,,∴
.
在中,,又,
∴
.
根据条件还可以得出,,.
A.在中,,
∴
,故选项A正确.
B.,故选项B错误.
C.,故选项C错误.
D.∵
,∴
,故选项D错误.
8.A
解析:先由坡比的定义,得BC∶AC=1∶.由BC=6
m,可得AC=6
m.
在Rt△ABC中,由勾股定理,得AB==12(m).
9.B
解析:设小球距离地面的高度为则小球水平移动的距离为
所以解得
10.B
解析:设
又因为在菱形中,所以所以
所以由勾股定理知所以2
11.A
解析:设直角三角形的两直角边长分别为则
所以斜边长
12.B
解析:在锐角三角函数中仅当∠45°时,,所以选项错误;
因为45°<∠A<90°,所以∠B<45°,即∠A>∠B,所以BC>AC,所以>,即,所以选项正确,选项错误;
>1,<1,所以选项错误.
13.>
解析:因为,所以∠.
14.
解析:过F点作FG∥BC交AB于点G.
∵
在△ABC中,AB=AC,AD是BC边上的中线,
∴
BD=CD=BC=1,∠BAD=∠CAD=∠BAC=15°,AD⊥BC.
∵
∠ACE=∠BAC,
∴
∠CAD=∠ACE=15°,
∴
AF=CF.
∵
∠ACD=(180°-30°)÷2=75°,
∴
∠DCE=75°-15°=60°.
在Rt△CDF中,
CF=
=2,DF=CD·tan
60°=.
又AF=CF,∴
AF=2.
∵
FG∥BC,
∴
GF∶BD=AF∶AD,即GF∶1=2∶(2+),
解得GF=4-2,
∴
EF∶EC=GF∶BC,即EF∶(EF+2)=(4-2)∶2,
解得EF=-1.
15.43.3
解析:因为,所以
所以所以.
16.15°或75°
解析:如图,.
在图①中,,所以∠∠;
在图②中,,所以∠∠.
17.76
解析:如图,因为,所以CD=12,
由勾股定理得所以这个风车的外围周长为
18.②③④
解析:因为∠C=90°,AB=2BC,所以∠A=30°,∠B=60°,所以②③④正确.
19.解:(1)
(2).
20.分析:由sin
A==求出BC的长,根据勾股定理求出AC的长,利用tan
B=求出tan
B的值.
解:∵
sin
A==,AB=10,∴
BC=4.
又∵
AC==2,∴
tan
B==.
21.分析:(1)如图,过点P作PD⊥AB于点D,设PD=
km,根据AD+BD=2列方程求解.
(2)过点B作BF⊥CA于点F,在Rt△ABF和Rt△BFC中解直角三角形求解.
解:(1)如图,过点P作PD⊥AB于点D,
设PD=
km,由题意可知∠PBD=45°,∠PAD=30°,
∴
在Rt△BDP中,BD=PD=
km,在Rt△PDA中,AD=PD=
km.
∵
AB=2
km,∴
=2.∴
==1.
∴
点P到海岸线l的距离为()km.
(2)如图,过点B作BF⊥CA于点F.
在Rt△ABF中,BF=AB·sin
30°=2×=1(km).
在△ABC中,∠C=180°∠BAC∠ABC=45°.
在Rt△BFC中,BC=BF=×1=(km).
∴
点C与点B之间的距离为
km.
点拨:此题是解直角三角形在现实生活中的应用,通过构造直角三角形求解.当利用勾股定理或锐角三角函数不能直接求解时,常采用作垂线、引入未知数(一般为待定的数)构造方程求解.
22.解:设,则由题意可知,m.
在Rt△AEC中,tan∠CAE=,即tan
30°=,
∴,即3x(x+100),解得x50+50.
经检验50+50是原方程的解.
∴
故该建筑物的高度约为
23.解:(1)∵
,∴
∠∠.
∵
∥,∴
∠∠∠.
在梯形中,∵
,∴
∠∠∠∠
∵
,∴
3∠
,
∴
∠30°
,∴
(2)如图,过点作于点.
在Rt△中,?
∠,
?
∠,∴
在Rt△中,,
∴
梯形的面积为
24.分析:利用解直角三角形求线段长,首先根据锐角三角函数的定义选取恰当的三角函数关系式,然后把已知的数据代入计算.本题根据锐角三角函数的定义得tan
37°=,把,BC=20
m代入tan
37°=中求出树的高度AB.
解:因为tan
37°=≈0.75,BC=20
m,所以AB≈0.75×20=15(m).
25.解:过点作于点..
因为∠,300
m,
所以300(-1)即热气球的升空点与着火点的距离为300(-1)
26.(1)解:1,;
(2)解:①∵
∠A<∠BOC60,∴
∠A不可能是直角.
②当∠ABP90时,如图所示(第26题答图(1)),
∵
∠BOC60,∴
∠OPB30.
∴
OP2OB,即2t2.∴
t1.
第26题答图(1)
③当∠APB90时,如图所示(第26题答图(2)),作PD⊥AB,垂足为D,则∠ADP∠PDB90.
在Rt△POD中,∵
∠POD=60,∴
∠OPD=30.
∵
OP2t,
∴
ODt,PDt,AD2t,BD1t(△BOP是锐角三角形).
第26题答图(2)
方法一:BP2BD2+PD2=(1t)23t2,AP2AD2+PD2=(2t)23t2.
∵
BP2AP2AB2,∴
(1t)23t2(2t)23t29,即4t2t20.
解得t1,t2(舍去).
方法二:∵
∠APD∠BPD90,∠B∠BPD90,
∴
∠APD∠B.∴
△APD∽△PBD.
∴
∴
PD2AD·BD.
于是(t)2(2t)(1t),即4t2t20.
解得t1,t2(舍去).
综上,当△ABP为直角三角形时,t1或.
(3)证法一:∵
APAB,∴
∠APB∠B.
如图所示(第26题答图(3)),作OE∥AP,交BP于点E,
∴
∠OEB∠APB∠B.
∵
AQ∥BP,∴
∠QAB∠B180.
又∵
∠3∠OEB180,∴
∠3∠QAB.
又∵
∠AOC∠2∠B∠1∠QOP,∠B∠QOP,
∴
∠1∠2.
在△QAO和△OEP中,∵
∠3∠QAO,∠1∠2,
∴
△QAO∽△OEP.
∴
,即AQ·EPEO·AO.
∵
OE∥AP,∴
△OBE∽△ABP.
∴
.∴
OEAP1,BPEP.
∴
AQ·BPAQ·EP
AQ·EPAO·EO213.
第26题答图(3)
证法二:如图所示(第26题答图(4)),连接PQ,设AP与OQ相交于点F.
∵
AQ∥BP,∴
∠QAP∠APB.
∵
APAB,∴
∠APB∠B.∴
∠QAP∠B.
又∵
∠QOP∠B,∴
∠QAP∠QOP.
在△QFA和△PFO中,∵
∠QAF∠FOP,∠QFA∠PFO,
∴
△QFA∽△PFO.∴
,即.
又∵
∠PFQ∠OFA,∴
△PFQ∽△OFA.∴
∠3∠1.
∵
∠AOC∠2∠B∠1∠QOP,∠B∠QOP,
∴
∠1∠2.∴
∠2∠3.
∴
△APQ∽△BPO.∴
.∴
AQ·BPAP·BO313.
第26题答图(4)
第3题图
第5题图
第8题图
第9题图
A
B
C
第12题图
①1
A
B
C
②2
A
B
C
第17题图
第14题图
B
C
A
东
西
45°
60°
第25题图
第24题图
第4题答图
第14题答图
第16题答图
B
C
D
②
A
A
B
C
D
①
A
B
C
D
第17题答图
第21题答图
4
