安徽省亳州市2020-2021学年第一学期九年级第二次月考数学试卷(word版,含答案)
文档属性
| 名称 | 安徽省亳州市2020-2021学年第一学期九年级第二次月考数学试卷(word版,含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 562.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-12 00:00:00 | ||
图片预览


文档简介
2020-2021学年度第一学期九年级质量检测试卷(二)
数学(沪科版)
注意事项:
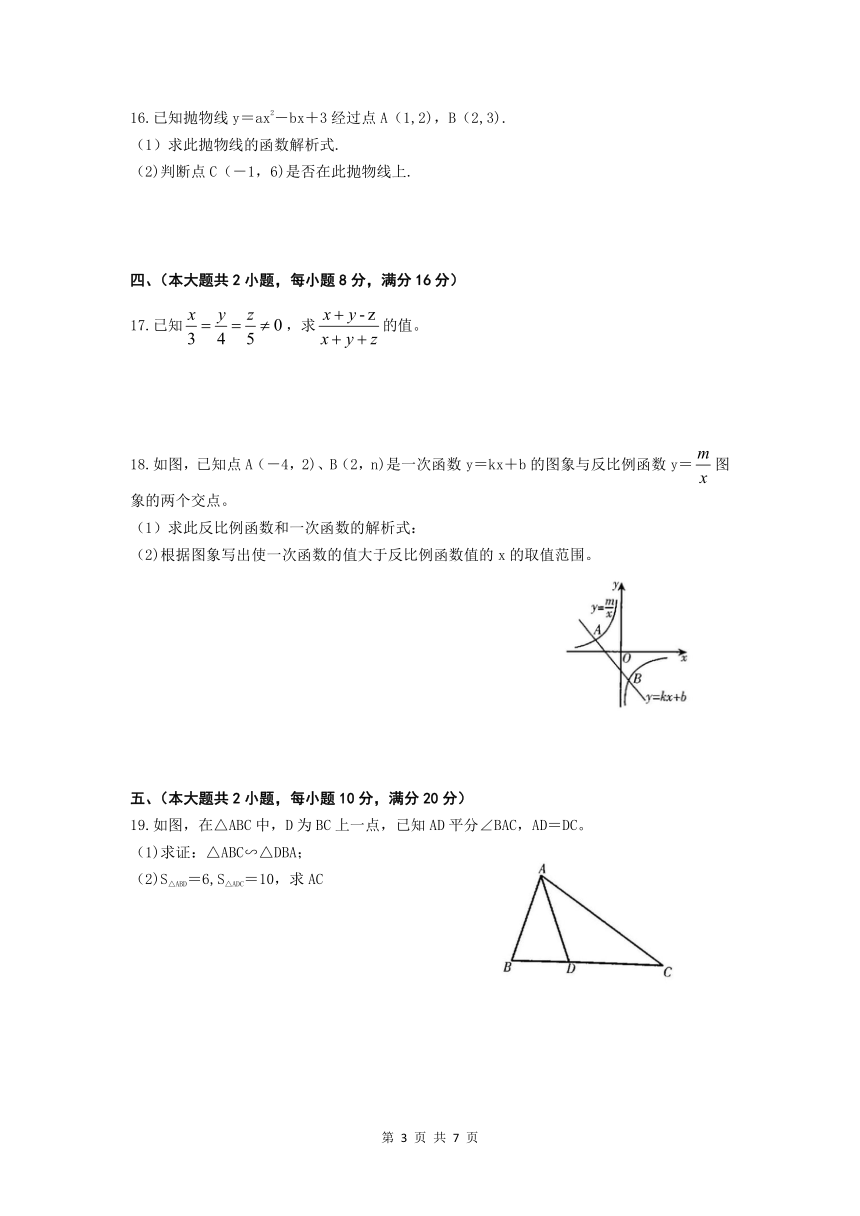
1.你拿到的试卷满分为150分,考试时间为120分钟。
2.本试卷包括“试题卷”和“答题卷”两部分。“试题卷”共4页,“答题卷”共6页。
3.请务必在“答题卷”上答题,在“试题卷”上答题是无效的。
4.考试结束后,请将“试题卷”和“答题卷”一并交回。
一、选择题(本大题共10小题,每小题4分,共40分)
1.若两个相似三角形的对应中线的比为3:4,则它们的对应角平分线的比为(
)
A.1:16
B.16:9
C.4:3
D.3:4
2.将二次函数y=x的图象向左平移2个单位,则平移后的二次函数的解析式为(
)
A.y=x2-2
B.y=x2+2
C.y=(x-2)2
D.y=(x+2)2
3.已知3x=5y(y≠0),则下列比例式成立的是(
)
A.
B.
C.
D.
4.如图,Rt△OAB的直角边OA=2,AB=1,OA在数轴上,在OB上截取BC=BA,以原点O为圆心,OC为半径画弧,交数轴于点P,则OP的中点D对应的实数是(
)
A.
B.
C.
D.
5.若点(x1,y1)、(x2,y2)和(x3,y3)分别在反比例函数的图象上,且x1<x2<0<x3,则下列判断中正确的是(
)
A.y1<y2<y3
B.y3<y1<y2
C.y2<y3<y1
D.y3<y2<y1
6.已知△ABC∽△A?B?C,AB=8,A?B?=6,则△ABC与△A?B?C的周长之比为(
)
A.
B.
C.
D.
7.下列四组线段中,能构成比例线段的一组是(
)
A.1cm,3cm,3cm,6cm
B.4cm,5cm,6cm,7cm
C.2cm,3cm,4cm,6cm
D.1cm,1.5cm,3cm,3.5cm
8.若抛物线y=x2-2x+c与y轴的交点为(0,-3),则下列说法不正确的是(
)
A.抛物线开口向上
B.抛物线的对称轴是x=1
C.当x=1时,y的最大值为-4
D.抛物线与x轴的交点为(-1,0),(3,0)
9.如果用线段a、b、c,求作线段x,使a:b=c:x,那么下列作图正确的是(
)
10.如图,直线l和双曲线(k>0)交于A、B两点,P是线段AB上的点(不与A、B重合),过点A、B、P分别向x轴作垂线,垂足分别为C、D、E,连接OA、OB、OP,设△AOC的面积为S1、△BOD的面积为S2、△POE的面积为S3,则(
)
A.S1<S2<S3
B.S1>S2>S3
C.S1=S2>S3
D.S1=S2<S3
二、填空题(本大题共4小题,每小题5分,共20分)
11.二次函数y=-x2+2x-2的图像的顶点坐标为_______________。
12.如图,请补充一个条件_______________,使△ACB∽△ADE.
13.如图,若点A的坐标位(2-,0),则点B的坐标为______________。
14.如图,AC与BE交于点D,∠A=∠E=90°,若点D是线段AC的中点,且AB=AC=10.则BE的长等于______________。
三、(本大题共2小题,每小题8分,满分16分)
15.如图,图中小方格都是边长为1的正方形,△ABC与△A?B?C?是关于点O为位似中心的
位似图形,它们的顶点都在小正方形顶点上.
(1)画出位似中心点0;
(2)△ABC与△A?B?C?的位似比为_____________。
16.已知抛物线y=ax2-bx+3经过点A(1,2),B(2,3).
(1)求此抛物线的函数解析式.
(2)判断点C(-1,6)是否在此抛物线上.
四、(本大题共2小题,每小题8分,满分16分)
17.已知,求的值。
18.如图,已知点A(-4,2)、B(2,n)是一次函数y=kx+b的图象与反比例函数y=图象的两个交点。
(1)求此反比例函数和一次函数的解析式:
(2)根据图象写出使一次函数的值大于反比例函数值的x的取值范围。
五、(本大题共2小题,每小题10分,满分20分)
19.如图,在△ABC中,D为BC上一点,已知AD平分∠BAC,AD=DC。
(1)求证:△ABC∽△DBA;
(2)S△ABD=6,S△ADC=10,求AC
20.如图,AB·AE=AD·AC,且∠1=∠2,求证:△ABC∽△ADE。
六、(本题满分12分)
21.某商店经销一种学生用双肩包,已知这种双肩包的成本价为每个20元.市场调查发现,这种双肩包每天的销售量y(个)与销售单价x(元)有如下关系:y=-x+60(20≤x≤60).
设这种双肩包每天的销售利润为w元
(1)求w与x之间的函数关系式;
(2)这种双肩包销售单价定为多少元时,每天的销售利润最大?最大利润是多少元?
七、(本题满分12分)
22.如图,点E是正方形ABCD的边BC的中点,点F在边DC上,且DF=3CF,连接EF并延
长交AD的延长线于点G。
(1)求证:△ABE∽△ECF;
(2)若正方形的边长为2,求AG的长。
八、(本题满分14分)
23.在Rt△ABC中,∠C=90°,AC=10cm,BC=8cm,现有动点P从点A出发,沿AC向点C方向运动,动点Q从点C出发,沿线段CB也向点B方向运动,如果点P的速度是2cm/秒,
点Q的速度是1cm/秒,它们同时出发,当有一点到达所在线段的端点时,就停止运动。设运动时间为t秒。求:
(1)当t=3时,这时,P,Q两点之间的距离是多少?
(2)若△CPQ的面积为S,求S关于t的函数关系式;
(3)当t为多少秒时,以点C,P,Q为顶点的三角形与△ABC相似?
2020—2021学年度第一学期九年级质量检测试卷(二)参考答案
数学(沪科版)
1-5.DDBAB
6-10.CCCBD
11.(1,-1)。
12.∠ADE=∠C或∠AED=∠B或
13.(,0)。
14.。
15.解:(1)如图所示:点O即为所求.
(2)∵
∴与的位似比为1∶2.
故答案为1∶2.
16.解:(1)抛物线经过点A(1,2),B(2,3),
解得
所以,抛物线的解析式为;
(2)∵当时,y=1+2+3=6,
∴点C(﹣1,6)在此抛物线上.
17.解:设(k≠0),
则x=3k,y=4k,z=5k,
所以,
18.解:(1)∵点A(﹣4,2)和点B(2,n)都在反比例函数的图像上,
∴解得∴反比例函数的解析式为:y=,
又由点A(﹣4,2)和点B(2,﹣4)都在反比例函数y=kx+b的图像上,
∴
∴一次函数的解析式为。
(2)一次函数的值大于反比例函数值的x的取值范围:x<﹣4或0<x<2。
19.解:(1)证明:∵AD平分∠BAC,∴∠BAD=∠CAD,
∵AD=DC,∴∠C=∠CAD,∴∠C=∠BAD,
∵∠B=∠B,∴△ABC∽△DBA;
(2)由(1)可知:△ABC∽△DBA,∴,
∵S△ABD=6,S△ADC=10,∴,∴,∴,
∵AD=DC,∴。
20.【解答】证明:如图,∵AB?AE=AD?AC,∴。
又∵∠1=∠2,∴∠2+∠BAE=∠1+∠BAE,即∠BAC=∠DAE,
∴△ABC∽△AED。
21.(1)w=(x﹣20)?y=(﹣x+60)(x﹣20)=﹣x2+20x+60x﹣1200=﹣x2+80x﹣1200,
w与x之间的函数解析式w=﹣x2+80x﹣1200;
(2)根据题意得:w=﹣x2+80x﹣1200=﹣(x﹣40)2+400,
∵﹣1<0,当x=40时,w有最大值,最大值是400.
22.解:(1)证明:∵四边形ABCD是正方形,∴AB=BC=CD,∠B=∠C=90°,
∵点E是正方形ABCD边BC的中点,点F在边CD上,且DF=3CF,
∴,∴△ABE∽△ECF;
(2))解:∵△ABE∽△ECF,∴∠BAE=∠CEF,
∵四边形ABCD是正方形,且正方形ABCD的边长为2
∴AB=BC=CD=AD=2,BC∥AD,
∵E为BC中点,∴CE=BE=1,
∵BC∥AD,∴△ECF∽△GDF,
∵DF=3CF,
∴
∴DG=3CE=3×1=3,∴AG=AD+DG=3+2=5,
即AG=5。
23.解:由题意得AP=2t,CQ=t,则CP=10﹣2t,
(1)当t=3秒时,CP=10﹣2t=4cm,CQ=t=3cm,
由勾股定理得PQ=5;
(2)由题意得AP=2t,CQ=
t,则CP=10﹣2t,
因此Rt△CPQ的面积为S=(0≤t≤5)cm2;
(3)分两种情况:
①当Rt△CPQ∽Rt△CAB时,,即,解得t=秒;
②当Rt△CPQ∽Rt△CBA时,,即,解得t=秒。
因此t=秒或t=秒时,以点C、P、Q为顶点的三角形与△ABC相似。
数学(沪科版)
注意事项:
1.你拿到的试卷满分为150分,考试时间为120分钟。
2.本试卷包括“试题卷”和“答题卷”两部分。“试题卷”共4页,“答题卷”共6页。
3.请务必在“答题卷”上答题,在“试题卷”上答题是无效的。
4.考试结束后,请将“试题卷”和“答题卷”一并交回。
一、选择题(本大题共10小题,每小题4分,共40分)
1.若两个相似三角形的对应中线的比为3:4,则它们的对应角平分线的比为(
)
A.1:16
B.16:9
C.4:3
D.3:4
2.将二次函数y=x的图象向左平移2个单位,则平移后的二次函数的解析式为(
)
A.y=x2-2
B.y=x2+2
C.y=(x-2)2
D.y=(x+2)2
3.已知3x=5y(y≠0),则下列比例式成立的是(
)
A.
B.
C.
D.
4.如图,Rt△OAB的直角边OA=2,AB=1,OA在数轴上,在OB上截取BC=BA,以原点O为圆心,OC为半径画弧,交数轴于点P,则OP的中点D对应的实数是(
)
A.
B.
C.
D.
5.若点(x1,y1)、(x2,y2)和(x3,y3)分别在反比例函数的图象上,且x1<x2<0<x3,则下列判断中正确的是(
)
A.y1<y2<y3
B.y3<y1<y2
C.y2<y3<y1
D.y3<y2<y1
6.已知△ABC∽△A?B?C,AB=8,A?B?=6,则△ABC与△A?B?C的周长之比为(
)
A.
B.
C.
D.
7.下列四组线段中,能构成比例线段的一组是(
)
A.1cm,3cm,3cm,6cm
B.4cm,5cm,6cm,7cm
C.2cm,3cm,4cm,6cm
D.1cm,1.5cm,3cm,3.5cm
8.若抛物线y=x2-2x+c与y轴的交点为(0,-3),则下列说法不正确的是(
)
A.抛物线开口向上
B.抛物线的对称轴是x=1
C.当x=1时,y的最大值为-4
D.抛物线与x轴的交点为(-1,0),(3,0)
9.如果用线段a、b、c,求作线段x,使a:b=c:x,那么下列作图正确的是(
)
10.如图,直线l和双曲线(k>0)交于A、B两点,P是线段AB上的点(不与A、B重合),过点A、B、P分别向x轴作垂线,垂足分别为C、D、E,连接OA、OB、OP,设△AOC的面积为S1、△BOD的面积为S2、△POE的面积为S3,则(
)
A.S1<S2<S3
B.S1>S2>S3
C.S1=S2>S3
D.S1=S2<S3
二、填空题(本大题共4小题,每小题5分,共20分)
11.二次函数y=-x2+2x-2的图像的顶点坐标为_______________。
12.如图,请补充一个条件_______________,使△ACB∽△ADE.
13.如图,若点A的坐标位(2-,0),则点B的坐标为______________。
14.如图,AC与BE交于点D,∠A=∠E=90°,若点D是线段AC的中点,且AB=AC=10.则BE的长等于______________。
三、(本大题共2小题,每小题8分,满分16分)
15.如图,图中小方格都是边长为1的正方形,△ABC与△A?B?C?是关于点O为位似中心的
位似图形,它们的顶点都在小正方形顶点上.
(1)画出位似中心点0;
(2)△ABC与△A?B?C?的位似比为_____________。
16.已知抛物线y=ax2-bx+3经过点A(1,2),B(2,3).
(1)求此抛物线的函数解析式.
(2)判断点C(-1,6)是否在此抛物线上.
四、(本大题共2小题,每小题8分,满分16分)
17.已知,求的值。
18.如图,已知点A(-4,2)、B(2,n)是一次函数y=kx+b的图象与反比例函数y=图象的两个交点。
(1)求此反比例函数和一次函数的解析式:
(2)根据图象写出使一次函数的值大于反比例函数值的x的取值范围。
五、(本大题共2小题,每小题10分,满分20分)
19.如图,在△ABC中,D为BC上一点,已知AD平分∠BAC,AD=DC。
(1)求证:△ABC∽△DBA;
(2)S△ABD=6,S△ADC=10,求AC
20.如图,AB·AE=AD·AC,且∠1=∠2,求证:△ABC∽△ADE。
六、(本题满分12分)
21.某商店经销一种学生用双肩包,已知这种双肩包的成本价为每个20元.市场调查发现,这种双肩包每天的销售量y(个)与销售单价x(元)有如下关系:y=-x+60(20≤x≤60).
设这种双肩包每天的销售利润为w元
(1)求w与x之间的函数关系式;
(2)这种双肩包销售单价定为多少元时,每天的销售利润最大?最大利润是多少元?
七、(本题满分12分)
22.如图,点E是正方形ABCD的边BC的中点,点F在边DC上,且DF=3CF,连接EF并延
长交AD的延长线于点G。
(1)求证:△ABE∽△ECF;
(2)若正方形的边长为2,求AG的长。
八、(本题满分14分)
23.在Rt△ABC中,∠C=90°,AC=10cm,BC=8cm,现有动点P从点A出发,沿AC向点C方向运动,动点Q从点C出发,沿线段CB也向点B方向运动,如果点P的速度是2cm/秒,
点Q的速度是1cm/秒,它们同时出发,当有一点到达所在线段的端点时,就停止运动。设运动时间为t秒。求:
(1)当t=3时,这时,P,Q两点之间的距离是多少?
(2)若△CPQ的面积为S,求S关于t的函数关系式;
(3)当t为多少秒时,以点C,P,Q为顶点的三角形与△ABC相似?
2020—2021学年度第一学期九年级质量检测试卷(二)参考答案
数学(沪科版)
1-5.DDBAB
6-10.CCCBD
11.(1,-1)。
12.∠ADE=∠C或∠AED=∠B或
13.(,0)。
14.。
15.解:(1)如图所示:点O即为所求.
(2)∵
∴与的位似比为1∶2.
故答案为1∶2.
16.解:(1)抛物线经过点A(1,2),B(2,3),
解得
所以,抛物线的解析式为;
(2)∵当时,y=1+2+3=6,
∴点C(﹣1,6)在此抛物线上.
17.解:设(k≠0),
则x=3k,y=4k,z=5k,
所以,
18.解:(1)∵点A(﹣4,2)和点B(2,n)都在反比例函数的图像上,
∴解得∴反比例函数的解析式为:y=,
又由点A(﹣4,2)和点B(2,﹣4)都在反比例函数y=kx+b的图像上,
∴
∴一次函数的解析式为。
(2)一次函数的值大于反比例函数值的x的取值范围:x<﹣4或0<x<2。
19.解:(1)证明:∵AD平分∠BAC,∴∠BAD=∠CAD,
∵AD=DC,∴∠C=∠CAD,∴∠C=∠BAD,
∵∠B=∠B,∴△ABC∽△DBA;
(2)由(1)可知:△ABC∽△DBA,∴,
∵S△ABD=6,S△ADC=10,∴,∴,∴,
∵AD=DC,∴。
20.【解答】证明:如图,∵AB?AE=AD?AC,∴。
又∵∠1=∠2,∴∠2+∠BAE=∠1+∠BAE,即∠BAC=∠DAE,
∴△ABC∽△AED。
21.(1)w=(x﹣20)?y=(﹣x+60)(x﹣20)=﹣x2+20x+60x﹣1200=﹣x2+80x﹣1200,
w与x之间的函数解析式w=﹣x2+80x﹣1200;
(2)根据题意得:w=﹣x2+80x﹣1200=﹣(x﹣40)2+400,
∵﹣1<0,当x=40时,w有最大值,最大值是400.
22.解:(1)证明:∵四边形ABCD是正方形,∴AB=BC=CD,∠B=∠C=90°,
∵点E是正方形ABCD边BC的中点,点F在边CD上,且DF=3CF,
∴,∴△ABE∽△ECF;
(2))解:∵△ABE∽△ECF,∴∠BAE=∠CEF,
∵四边形ABCD是正方形,且正方形ABCD的边长为2
∴AB=BC=CD=AD=2,BC∥AD,
∵E为BC中点,∴CE=BE=1,
∵BC∥AD,∴△ECF∽△GDF,
∵DF=3CF,
∴
∴DG=3CE=3×1=3,∴AG=AD+DG=3+2=5,
即AG=5。
23.解:由题意得AP=2t,CQ=t,则CP=10﹣2t,
(1)当t=3秒时,CP=10﹣2t=4cm,CQ=t=3cm,
由勾股定理得PQ=5;
(2)由题意得AP=2t,CQ=
t,则CP=10﹣2t,
因此Rt△CPQ的面积为S=(0≤t≤5)cm2;
(3)分两种情况:
①当Rt△CPQ∽Rt△CAB时,,即,解得t=秒;
②当Rt△CPQ∽Rt△CBA时,,即,解得t=秒。
因此t=秒或t=秒时,以点C、P、Q为顶点的三角形与△ABC相似。
同课章节目录
