北师大版九年级数学上册第五章投影与视图知识精讲(附答案)
文档属性
| 名称 | 北师大版九年级数学上册第五章投影与视图知识精讲(附答案) |  | |
| 格式 | zip | ||
| 文件大小 | 575.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-12 15:56:29 | ||
图片预览



文档简介
第五章
视图与投影
知识要点
1.
主要概念:
(1)圆柱的主视图是矩形,左视图是矩形,俯视图是圆。
(2)圆锥的主视图是三角形;左视图是三角形;俯视图是圆,还要画上圆心。
(3)球的主视图是圆;左视图是圆;俯视图是圆。
(4)投影:物体在光线的照射下,会在地面或墙上留下它的影子,这就是投影现象。
(5)平行投影:太阳光线可以看成是平行光线,像这样的光线所形成的投影称为平行投影。
(6)中心投影:由一点发出的光线形成的投影是中心投影。
(7)视点:眼睛的位置称为视点。
(8)视线:由视点出发的线称为视线。
(9)盲区:视线看不到的地方称为盲区。
2.
主要原理:
(1)画视图时,看得见的部分的轮廓通常画成实线,看不见部分的轮廓线通常画成虚线。
(2)我们在画三视图时,主、左视图的高要相等;俯、左视图的宽要相等。
(3)在同一时刻,不同物体的影子与它们的高度是成比例的。
(4)在同一天中,由早晨到傍晚,物体的影子由正西、北偏西、正北、北偏东、正东的方向移动。
(5)当投影光线与投影面垂直时,形成的投影就是物体的正投影。
【典型例题】
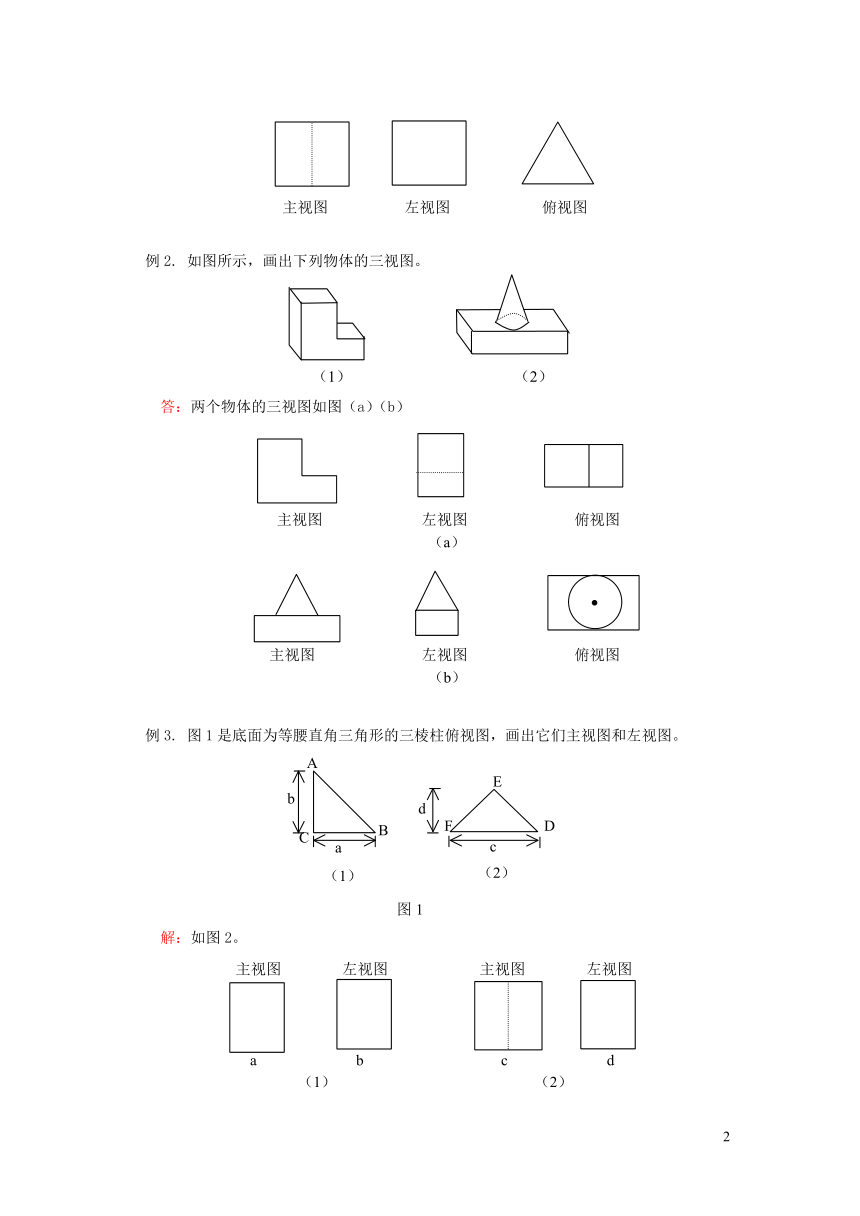
例1.
如图,画出正三棱柱在这两种位置时的视图。
解:图中正三棱柱在位置(一)时的三视图如下图所示。
图中正三棱柱在位置(二)时的三视图如下图所示:
例2.
如图所示,画出下列物体的三视图。
答:两个物体的三视图如图(a)(b)
例3.
图1是底面为等腰直角三角形的三棱柱俯视图,画出它们主视图和左视图。
解:如图2。
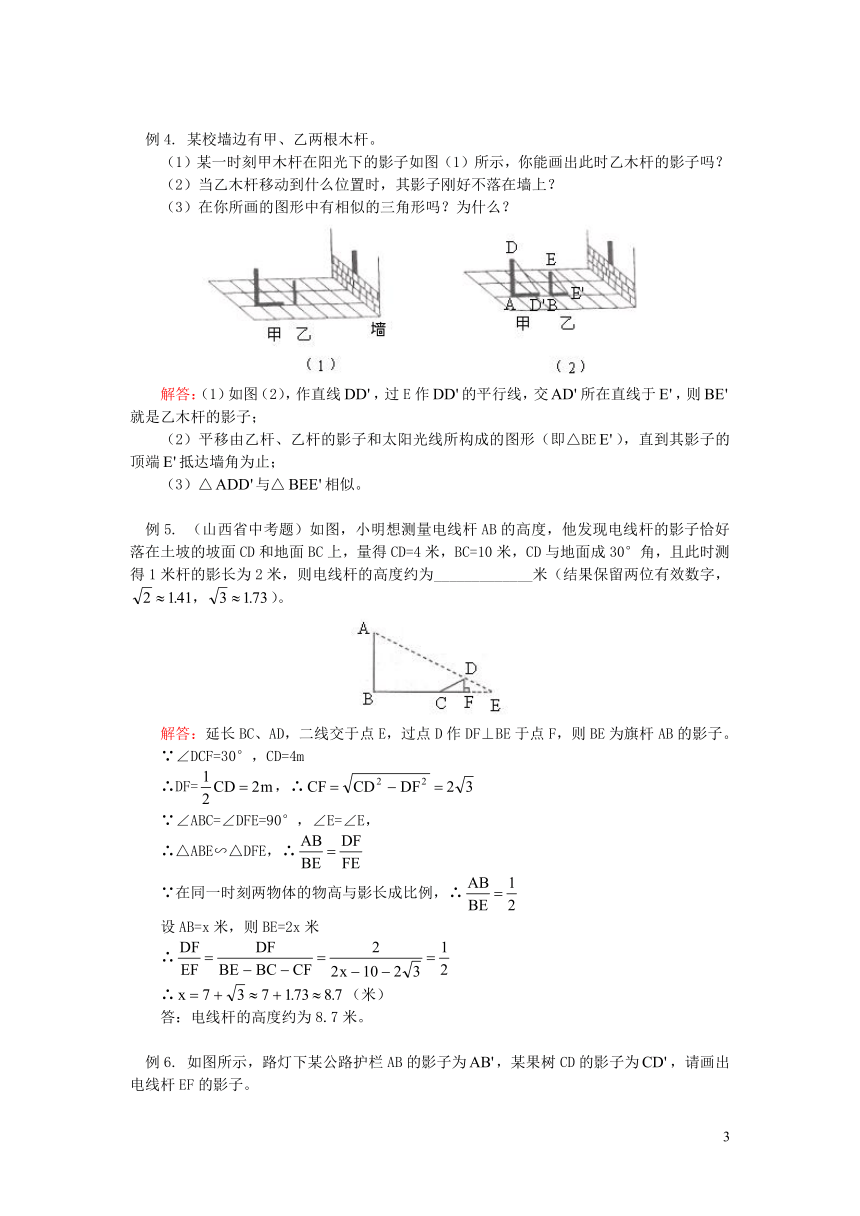
例4.
某校墙边有甲、乙两根木杆。
(1)某一时刻甲木杆在阳光下的影子如图(1)所示,你能画出此时乙木杆的影子吗?
(2)当乙木杆移动到什么位置时,其影子刚好不落在墙上?
(3)在你所画的图形中有相似的三角形吗?为什么?
解答:(1)如图(2),作直线,过E作的平行线,交所在直线于,则就是乙木杆的影子;
(2)平移由乙杆、乙杆的影子和太阳光线所构成的图形(即△BE),直到其影子的顶端抵达墙角为止;
(3)△与△相似。
例5.
(山西省中考题)如图,小明想测量电线杆AB的高度,他发现电线杆的影子恰好落在土坡的坡面CD和地面BC上,量得CD=4米,BC=10米,CD与地面成30°角,且此时测得1米杆的影长为2米,则电线杆的高度约为_____________米(结果保留两位有效数字,)。
解答:延长BC、AD,二线交于点E,过点D作DF⊥BE于点F,则BE为旗杆AB的影子。
∵∠DCF=30°,CD=4m
∴DF=,∴
∵∠ABC=∠DFE=90°,∠E=∠E,
∴△ABE∽△DFE,∴
∵在同一时刻两物体的物高与影长成比例,∴
设AB=x米,则BE=2x米
∴
∴(米)
答:电线杆的高度约为8.7米。
例6.
如图所示,路灯下某公路护栏AB的影子为,某果树CD的影子为,请画出电线杆EF的影子。
解答:如图所示,作直线,交于点O,连结OF并延长交AE于,即为EF的影子。
例7.
同一时刻,一棵树和一竿旗的影子如图所示,这是白天还是夜晚,请画出小明此刻的影子。
解:是夜晚,分别过小树及其影子顶端,旗杆及其影子顶端作直线交点为O,过O点及小明头部顶点作直线,此直线与地面交于点B,设小明立足点为A,则AB是小明的影子。
例8.
与一盏路灯相对,有一玻璃幕墙,幕墙前面的地面上有一盆花和一棵树。晚上,幕墙反射路灯灯光形成了那盆花的影子,树影是路灯灯光形成的,如下图所示,你能确定此时路灯光源的位置吗?
解:过盆花及其影子顶端作直线,作反射面法线,作∠2=∠1,得光线l1,过树及其影子顶端作直线l2,两线交点O,则O处为灯光位置。
例9.
小明、小刚在同一座楼的四层、六层。他们楼前有一商店,他们的同学小江在下面喊,小明说,小江在哪儿呢?小刚说我看到小江啦!请问此时小江在什么位置?
解:将六楼处设为点A,四楼处设为点,商店顶部一点设为点B,过A、B,、B分别作直线交地面于C、D两点,如图所示。小江在CD区域内。
真题演练
一、选择题
1.
如图(1)所示,所对应的物体还是图(2)所示中的(
)
图(1)
图(2)
2.
如图(3)所示的空心几何体的俯视图是图(4)中的(
)
图(3)
图(4)
3.
物体在太阳光的照射下,不同的时刻会发生的现象是(
)
A.
影子的大小不变,方向在变
B.
影子的大小在变,方向不变
C.
影子的大小、方向都在变
D.
影子的大小、方向都不变
4.
强强和亮亮在路灯下走,本来很高的强强的影长却比矮的亮亮的影子短,因为(
)
A.
强强离路灯近
B.
亮亮离路灯近
C.
强强和亮亮分别在路灯的两旁
D.
路灯比强强高
5.
货车司机的驾驶室一般都设计得较高,而且尽量靠前,这是为了(
)
A.
接触到更好的阳光
B.
看得更远
C.
减小因车头挡住视线产生的盲区
D.
空气更新鲜
6.
下列投影中,不属于中心投影的是(
)
A.
晚上路灯下小孩的影子
B.
汽车灯光照射下行人的影子
C.
阳光下沙滩上人的影子
D.
舞台上一束灯光下演员的影子
7.
小明拿了一张正方形卡片,使卡片面与墙面平行,这时发现墙面上形成了卡片的影子,则下列关于其影子的叙述正确的是(
)
A.
墙上形成的影子的形状和大小一定与卡片相同
B.
墙上形成的影子有可能比卡片小
C.
墙上形成的影子比卡片大或小都有可能
D.
墙上形成的影子有可能比卡片大
8.一个几何体的主视图和左视图都是相同的长方形,府视图为圆,则这个几何体为(
)
A、圆柱
B、圆锥
C、圆台
D、球
9.从早上太阳升起的某一时刻开始到晚上,旭日广场的旗杆在地面上的影子的变化规律是(
)
A、先变长,后变短
B、先变短,后变长
C、方向改变,长短不变
D、以上都不正确
10.在相同的时刻,物高与影长成比例.如果高为1.5米人测竿的影长为2.5米,那么影长为30米的旗杆的高是(
)
A、20米
B、16米
C、18米
D、15米
11.下列说法正确的是(
)
A、物体在阳光下的投影只与物体的高度有关
B、小明的个子比小亮高,我们可以肯定,不论什么情况,小明的影子一定比小亮的影子长.
C、物体在阳光照射下,不同时刻,影长可能发生变化,方向也可能发生变化.
D、物体在阳光照射下,影子的长度和方向都是固定不变的.
12.关于盲区的说法正确的有(
)
(1)我们把视线看不到的地方称为盲区
(2)我们上山与下山时视野盲区是相同的
(3)我们坐车向前行驶,有时会发现一些高大的建筑物会被比它矮的建筑物挡住
(4)人们常说“站得高,看得远”,说明在高处视野盲区要小,视野范围大
A、1
个
B、2个
C、3个
D、4个
13.如图1是空心圆柱体在指定方向上的视图,正确的是(
)
图1
14.如图2所示,这是圆桌正上方的灯泡(看作一个点)发
出的光线照射桌面后,在地面上形成阴影(圆形)的示意图.
已知桌面的直径为1.2m,桌面距离地面1m,若灯泡距离地
面3m,则地面上阴影部分的面积为(
)
图
2
A、0.36m2
B、0.81m2
C、2m2
D、3.24m2
15.如图3是小明一天上学、放学时看到的一根电线杆的影子的府视图,按时间先后顺序进行排列正确的是(
)
A、(1)(2)(3)(4)
B、(4)(3)(1)(2)
C、(4)(3)(2)(1)
D、(2)(3)(4)(1)
16.“皮影戏”作为我国一种民间艺术,对它的叙述错误的是(
)
A.它是用兽皮或纸板做成的人物剪影,来表演故事的戏曲
B.表演时,要用灯光把剪影照在银幕上
C.灯光下,做不同的手势可以形成不同的手影
D.表演时,也可用阳光把剪影照在银幕上
17.给出下列结论正确的有(
)
①物体在阳光照射下,影子的方向是相同的
②物体在任何光线照射下影子的方向都是相同的
③物体在路灯照射下,影子的方向与路灯的位置有关
④物体在光线照射下,影子的长短仅与物体的长短有关.
A.1个
B.2个
C.3个
D.4个
二、填空题
18.
明明和亮亮为了踢好足球,练习追逐跑,于是他们两人决定玩踩影子的游戏,即踩到对方影子为获胜,你认为在阳光下练习还是在路灯下练习更有意义?_____________。
19.
现有甲、乙两个长方体盒子,甲的规格为:15cm×40cm×60cm,乙的规格为:20cm×30cm×30cm。
(1)乙盒子____________(填“能”或“不能”)放在甲盒子中;
(2)在阳光下乙盒子的影子____________(填“能”或“不能”)藏在甲盒子的影子中。
20.
明明和爸爸玩将手影投在墙上的游戏,爸爸的手大,手影做出了一只大狗,明明的手小,但手影却做出了一只更大的狗,明明的手比爸爸手_____________(填“靠近”或“远离”)墙。
21.
阳光下,在同一时刻,物体越高,它的影子越_____________。在灯光下,物体的影长不仅与物体的_____________有关,还与物体到光源的_____________有关。
22.
三种视图都相同的几何体有_____________。
23.
根据下列物体的三视图,如图,可知几何体是_____________
1
24.主视图、左视图、府视图都相同的几何体为
(写出两个).
25、太阳光线形成的投影称为
,手电筒、路灯、台灯的光线形成的投影称为
.
26、我们把大型会场、体育看台、电影院建为阶梯形状,是为了
.
27、为了测量一根电线杆的高度,取一根2米长的竹竿竖直放在阳光下,2米长的竹竿的影长为1米,并且在同一时刻测得电线杆的影长为7.3米,则电线杆的高为
米.
28、如果一个几何体的主视图、左视图都是等腰三角形,俯视图为圆,那么我们可以确定这个几何体是
.
29、将一个三角板放在太阳光下,它所形成的投影是
,也可能是
.
30、身高相同的小明和小华站在灯光下的不同位置,如果小明离灯较远,那么小明的投影比小华的投影
.
31、展览厅内要用相同的正方体木块搭成一个三视图如图4的展台,则此展台共需这样的正方体______块。
32、一张桌子摆放若干碟子,从三个方向上看,三种视图如下图所示,则这张桌子上共
有
个碟子。
33、身高相同的小明和小丽站在灯光下的不同位置,已知小明的投影比小丽的投影长,我们可以判定小明离灯光较_________.
三、解答题
34.
如图,某汽车司机在平坦的公路上行驶,前面出现两个建筑物,在A处司机能看到甲建筑物的一部分(把汽车看成一个点),这时视线与公路夹角α=30°,乙建筑物的高度为15米,若汽车刚好看不到甲建筑物时,司机的视线与公路的夹角为45°,请问他行驶了多少千米?
35
如图所示,添线补全下列物体的三种视图:
36.
如图所示,分别是两根木杆及其影子的情形。
(1)哪个图形反映了阳光下的情形?哪个图反映了路灯下的情形?
(2)请你画出图中表示小树影长的线段。
37某个有阳光的上午,战士们队列整齐地在操场上做操,战士甲和战士乙在同一列,战士甲恰好能踩到战士乙的影子,但战士甲的影子却不能被他后面的战士踩到,你知道战士甲和战士乙谁高吗?为什么?
38
如图,某小区宿舍楼甲楼坐落在正南正北方向,楼高16m,现在要在甲楼后面盖一座乙楼,冬天太阳最低时的正午时刻,若两楼相距20m,则甲楼的影子将落在乙楼上6m,若使甲楼的影子刚好不影响乙楼的采光,那么两楼的距离应是多少米?
39、某糖果厂为儿童设计一种新型的装糖果的不倒翁(如图5所示)
请你为包装厂设计出它的主视图、左视图和府视图.
40、画出图6中三棱柱的主视图、左视图、俯视图.
41、画出图7中空心圆柱的主视图、左视图、俯视图.
42、如图8所示,屋顶上有一只小猫,院子里有一只小老鼠,若小猫看见了小老鼠,则小老鼠就会有危险,试画出小老鼠在墙的左端的安全区.
拓广探索(共20分)
43、如图9为住宅区内的两幢楼,它们的高AB=CD=30m,两楼间的距离AC=30m,现需了解甲楼对乙楼的采光的影响情况,(1)当太阳光与水平线的夹角为30°角时,求甲楼的影子在乙楼上有多高(精确到0.1m,1.73);(2)若要甲楼的影子刚好不落在乙楼的墙上,此时太阳与水平线的夹角为多少度?
44、阳光通过窗口照到教室内,竖直窗框在地面上留下2.1m长的影子[如图(10)所示],已知窗框的影子DE到窗下墙脚的距离CE=3.9m,窗口底边离地面的距离BC=1.2m,试求窗口的高度(即AB的值)
45、一位同学想利用有关知识测旗杆的高度,他在某一时刻测得高为0.5m的小木棒的影长为0.3m,但当他马上测量旗杆的影长时,因旗杆靠近一幢建筑物,影子不全落在地面上,有一部分影子在墙上,他先测得留在墙上的影子CD=1.0m,又测地面部分的影长BC=3.0m,你能根据上述数据帮他测出旗杆的高度吗?
46、学习投影后,小明、小颖利用灯光下自己的影子长度来测量一路灯的高度,并探究影子长度的变化规律.如图7,在同一时间,身高为的小明的影子长是,而小颖刚好在路灯灯泡的正下方点,并测得.
(1)请在图中画出形成影子的光线,交确定路灯灯泡所在的位置;
(2)求路灯灯泡的垂直高度;
(3)如果小明沿线段向小颖(点)走去,当小明走到中点处时,求其影子的长;当小明继续走剩下路程的到处时,求其影子的长;当小明继续走剩下路程的到处,…按此规律继续走下去,当小明走剩下路程的到处时,其影子的长为
m(直接用的代数式表示).
【试题答案】
一、
1.
A
2.
A
3.
D
4.
A
5.
C
6.
C
7.
D
8、A;9、B;10、C;11、C;12、C;13、C;14、B;15、B;16、D;17、B;
二、
18.
阳光下
19
(1)不能
(2)能
20.
远离
21.
长,高度,距离
22
球
23
五棱柱
24、正方体或圆;25、平行投影,中心投影;26、减小盲区;27、14.6;28、圆锥;29、三角形,一条线段;30、长31、10;32、12;133、远;
三、
34.
解:过甲、乙建筑物顶端B、C两点作直线交地面于D,则汽车行至D点时刚好看不到甲建筑物,且∠BDE=45°。
在Rt△ACF中,
∠A=30°,CF=15
∴
在Rt△CFD中,
∵∠BDE=45°,∴∠FCD=45°
∴FD=CF=15
∴DA=AF-DF=。
答:他行驶了米。
35
36
(1)上图为路灯下的情形
下图为阳光下的情形
(2)上图先找到灯泡的位置再画树影
下图找出太阳光的方向,作平行线得到树影
37
乙比甲高
38.
由已知条件可求影长与物高的比为2,所以要使乙楼恰好采光不受影响,两楼的距离应为32m。
39、
40、
41、
42、略
43、(1)如图2,延长OB交DC于E,作EF⊥AB,交AB于F,
在Rt△BEF中,∵EF=AC=30m,∠FEB=30°,∴BE=2BF.
设BF=x,则
BE=2x.
根据勾股定理知
BE2=BF2+EF2
∴(2x)2=x2+302
∴(负值舍去),∴(m)
因此,EC=30-17.3=12.7(m)。
(2)当甲幢楼的影子刚好落在点C处时,△ABC为等腰三角形,因此,当太阳光与水平线夹角为45°时,甲楼的影子刚好不落在乙楼的墙上。
44、解:由于阳光是平行光线,即AE∥BD,
所以∠AEC=∠BDC.
又因为∠C是公共角,
所以△AEC∽△BDC,从而有.
又AC=AB+BC,DC=EC-ED,EC=3.9,ED=2.1,BC=1.2,
于是有,解得
AB=1.4(m)。
答:窗口的高度为1.4m。
45、能。旗杆的高度为6.0m。
分析:本题可以通过小明的身高和他的影子找出光源(即灯泡)的位置,由于路灯光线的投影是中心投影,然后利用相似三角形对应边成比例进行计算即可
46、解:(1)连接CA并延长交HE于G(如图3)
(2)由题意得:,
,,(m).
(3),,
图4
俯视图
主视图
左视图
图5
图6
图7
图8
图9
图10
图11
图2
图3
1
视图与投影
知识要点
1.
主要概念:
(1)圆柱的主视图是矩形,左视图是矩形,俯视图是圆。
(2)圆锥的主视图是三角形;左视图是三角形;俯视图是圆,还要画上圆心。
(3)球的主视图是圆;左视图是圆;俯视图是圆。
(4)投影:物体在光线的照射下,会在地面或墙上留下它的影子,这就是投影现象。
(5)平行投影:太阳光线可以看成是平行光线,像这样的光线所形成的投影称为平行投影。
(6)中心投影:由一点发出的光线形成的投影是中心投影。
(7)视点:眼睛的位置称为视点。
(8)视线:由视点出发的线称为视线。
(9)盲区:视线看不到的地方称为盲区。
2.
主要原理:
(1)画视图时,看得见的部分的轮廓通常画成实线,看不见部分的轮廓线通常画成虚线。
(2)我们在画三视图时,主、左视图的高要相等;俯、左视图的宽要相等。
(3)在同一时刻,不同物体的影子与它们的高度是成比例的。
(4)在同一天中,由早晨到傍晚,物体的影子由正西、北偏西、正北、北偏东、正东的方向移动。
(5)当投影光线与投影面垂直时,形成的投影就是物体的正投影。
【典型例题】
例1.
如图,画出正三棱柱在这两种位置时的视图。
解:图中正三棱柱在位置(一)时的三视图如下图所示。
图中正三棱柱在位置(二)时的三视图如下图所示:
例2.
如图所示,画出下列物体的三视图。
答:两个物体的三视图如图(a)(b)
例3.
图1是底面为等腰直角三角形的三棱柱俯视图,画出它们主视图和左视图。
解:如图2。
例4.
某校墙边有甲、乙两根木杆。
(1)某一时刻甲木杆在阳光下的影子如图(1)所示,你能画出此时乙木杆的影子吗?
(2)当乙木杆移动到什么位置时,其影子刚好不落在墙上?
(3)在你所画的图形中有相似的三角形吗?为什么?
解答:(1)如图(2),作直线,过E作的平行线,交所在直线于,则就是乙木杆的影子;
(2)平移由乙杆、乙杆的影子和太阳光线所构成的图形(即△BE),直到其影子的顶端抵达墙角为止;
(3)△与△相似。
例5.
(山西省中考题)如图,小明想测量电线杆AB的高度,他发现电线杆的影子恰好落在土坡的坡面CD和地面BC上,量得CD=4米,BC=10米,CD与地面成30°角,且此时测得1米杆的影长为2米,则电线杆的高度约为_____________米(结果保留两位有效数字,)。
解答:延长BC、AD,二线交于点E,过点D作DF⊥BE于点F,则BE为旗杆AB的影子。
∵∠DCF=30°,CD=4m
∴DF=,∴
∵∠ABC=∠DFE=90°,∠E=∠E,
∴△ABE∽△DFE,∴
∵在同一时刻两物体的物高与影长成比例,∴
设AB=x米,则BE=2x米
∴
∴(米)
答:电线杆的高度约为8.7米。
例6.
如图所示,路灯下某公路护栏AB的影子为,某果树CD的影子为,请画出电线杆EF的影子。
解答:如图所示,作直线,交于点O,连结OF并延长交AE于,即为EF的影子。
例7.
同一时刻,一棵树和一竿旗的影子如图所示,这是白天还是夜晚,请画出小明此刻的影子。
解:是夜晚,分别过小树及其影子顶端,旗杆及其影子顶端作直线交点为O,过O点及小明头部顶点作直线,此直线与地面交于点B,设小明立足点为A,则AB是小明的影子。
例8.
与一盏路灯相对,有一玻璃幕墙,幕墙前面的地面上有一盆花和一棵树。晚上,幕墙反射路灯灯光形成了那盆花的影子,树影是路灯灯光形成的,如下图所示,你能确定此时路灯光源的位置吗?
解:过盆花及其影子顶端作直线,作反射面法线,作∠2=∠1,得光线l1,过树及其影子顶端作直线l2,两线交点O,则O处为灯光位置。
例9.
小明、小刚在同一座楼的四层、六层。他们楼前有一商店,他们的同学小江在下面喊,小明说,小江在哪儿呢?小刚说我看到小江啦!请问此时小江在什么位置?
解:将六楼处设为点A,四楼处设为点,商店顶部一点设为点B,过A、B,、B分别作直线交地面于C、D两点,如图所示。小江在CD区域内。
真题演练
一、选择题
1.
如图(1)所示,所对应的物体还是图(2)所示中的(
)
图(1)
图(2)
2.
如图(3)所示的空心几何体的俯视图是图(4)中的(
)
图(3)
图(4)
3.
物体在太阳光的照射下,不同的时刻会发生的现象是(
)
A.
影子的大小不变,方向在变
B.
影子的大小在变,方向不变
C.
影子的大小、方向都在变
D.
影子的大小、方向都不变
4.
强强和亮亮在路灯下走,本来很高的强强的影长却比矮的亮亮的影子短,因为(
)
A.
强强离路灯近
B.
亮亮离路灯近
C.
强强和亮亮分别在路灯的两旁
D.
路灯比强强高
5.
货车司机的驾驶室一般都设计得较高,而且尽量靠前,这是为了(
)
A.
接触到更好的阳光
B.
看得更远
C.
减小因车头挡住视线产生的盲区
D.
空气更新鲜
6.
下列投影中,不属于中心投影的是(
)
A.
晚上路灯下小孩的影子
B.
汽车灯光照射下行人的影子
C.
阳光下沙滩上人的影子
D.
舞台上一束灯光下演员的影子
7.
小明拿了一张正方形卡片,使卡片面与墙面平行,这时发现墙面上形成了卡片的影子,则下列关于其影子的叙述正确的是(
)
A.
墙上形成的影子的形状和大小一定与卡片相同
B.
墙上形成的影子有可能比卡片小
C.
墙上形成的影子比卡片大或小都有可能
D.
墙上形成的影子有可能比卡片大
8.一个几何体的主视图和左视图都是相同的长方形,府视图为圆,则这个几何体为(
)
A、圆柱
B、圆锥
C、圆台
D、球
9.从早上太阳升起的某一时刻开始到晚上,旭日广场的旗杆在地面上的影子的变化规律是(
)
A、先变长,后变短
B、先变短,后变长
C、方向改变,长短不变
D、以上都不正确
10.在相同的时刻,物高与影长成比例.如果高为1.5米人测竿的影长为2.5米,那么影长为30米的旗杆的高是(
)
A、20米
B、16米
C、18米
D、15米
11.下列说法正确的是(
)
A、物体在阳光下的投影只与物体的高度有关
B、小明的个子比小亮高,我们可以肯定,不论什么情况,小明的影子一定比小亮的影子长.
C、物体在阳光照射下,不同时刻,影长可能发生变化,方向也可能发生变化.
D、物体在阳光照射下,影子的长度和方向都是固定不变的.
12.关于盲区的说法正确的有(
)
(1)我们把视线看不到的地方称为盲区
(2)我们上山与下山时视野盲区是相同的
(3)我们坐车向前行驶,有时会发现一些高大的建筑物会被比它矮的建筑物挡住
(4)人们常说“站得高,看得远”,说明在高处视野盲区要小,视野范围大
A、1
个
B、2个
C、3个
D、4个
13.如图1是空心圆柱体在指定方向上的视图,正确的是(
)
图1
14.如图2所示,这是圆桌正上方的灯泡(看作一个点)发
出的光线照射桌面后,在地面上形成阴影(圆形)的示意图.
已知桌面的直径为1.2m,桌面距离地面1m,若灯泡距离地
面3m,则地面上阴影部分的面积为(
)
图
2
A、0.36m2
B、0.81m2
C、2m2
D、3.24m2
15.如图3是小明一天上学、放学时看到的一根电线杆的影子的府视图,按时间先后顺序进行排列正确的是(
)
A、(1)(2)(3)(4)
B、(4)(3)(1)(2)
C、(4)(3)(2)(1)
D、(2)(3)(4)(1)
16.“皮影戏”作为我国一种民间艺术,对它的叙述错误的是(
)
A.它是用兽皮或纸板做成的人物剪影,来表演故事的戏曲
B.表演时,要用灯光把剪影照在银幕上
C.灯光下,做不同的手势可以形成不同的手影
D.表演时,也可用阳光把剪影照在银幕上
17.给出下列结论正确的有(
)
①物体在阳光照射下,影子的方向是相同的
②物体在任何光线照射下影子的方向都是相同的
③物体在路灯照射下,影子的方向与路灯的位置有关
④物体在光线照射下,影子的长短仅与物体的长短有关.
A.1个
B.2个
C.3个
D.4个
二、填空题
18.
明明和亮亮为了踢好足球,练习追逐跑,于是他们两人决定玩踩影子的游戏,即踩到对方影子为获胜,你认为在阳光下练习还是在路灯下练习更有意义?_____________。
19.
现有甲、乙两个长方体盒子,甲的规格为:15cm×40cm×60cm,乙的规格为:20cm×30cm×30cm。
(1)乙盒子____________(填“能”或“不能”)放在甲盒子中;
(2)在阳光下乙盒子的影子____________(填“能”或“不能”)藏在甲盒子的影子中。
20.
明明和爸爸玩将手影投在墙上的游戏,爸爸的手大,手影做出了一只大狗,明明的手小,但手影却做出了一只更大的狗,明明的手比爸爸手_____________(填“靠近”或“远离”)墙。
21.
阳光下,在同一时刻,物体越高,它的影子越_____________。在灯光下,物体的影长不仅与物体的_____________有关,还与物体到光源的_____________有关。
22.
三种视图都相同的几何体有_____________。
23.
根据下列物体的三视图,如图,可知几何体是_____________
1
24.主视图、左视图、府视图都相同的几何体为
(写出两个).
25、太阳光线形成的投影称为
,手电筒、路灯、台灯的光线形成的投影称为
.
26、我们把大型会场、体育看台、电影院建为阶梯形状,是为了
.
27、为了测量一根电线杆的高度,取一根2米长的竹竿竖直放在阳光下,2米长的竹竿的影长为1米,并且在同一时刻测得电线杆的影长为7.3米,则电线杆的高为
米.
28、如果一个几何体的主视图、左视图都是等腰三角形,俯视图为圆,那么我们可以确定这个几何体是
.
29、将一个三角板放在太阳光下,它所形成的投影是
,也可能是
.
30、身高相同的小明和小华站在灯光下的不同位置,如果小明离灯较远,那么小明的投影比小华的投影
.
31、展览厅内要用相同的正方体木块搭成一个三视图如图4的展台,则此展台共需这样的正方体______块。
32、一张桌子摆放若干碟子,从三个方向上看,三种视图如下图所示,则这张桌子上共
有
个碟子。
33、身高相同的小明和小丽站在灯光下的不同位置,已知小明的投影比小丽的投影长,我们可以判定小明离灯光较_________.
三、解答题
34.
如图,某汽车司机在平坦的公路上行驶,前面出现两个建筑物,在A处司机能看到甲建筑物的一部分(把汽车看成一个点),这时视线与公路夹角α=30°,乙建筑物的高度为15米,若汽车刚好看不到甲建筑物时,司机的视线与公路的夹角为45°,请问他行驶了多少千米?
35
如图所示,添线补全下列物体的三种视图:
36.
如图所示,分别是两根木杆及其影子的情形。
(1)哪个图形反映了阳光下的情形?哪个图反映了路灯下的情形?
(2)请你画出图中表示小树影长的线段。
37某个有阳光的上午,战士们队列整齐地在操场上做操,战士甲和战士乙在同一列,战士甲恰好能踩到战士乙的影子,但战士甲的影子却不能被他后面的战士踩到,你知道战士甲和战士乙谁高吗?为什么?
38
如图,某小区宿舍楼甲楼坐落在正南正北方向,楼高16m,现在要在甲楼后面盖一座乙楼,冬天太阳最低时的正午时刻,若两楼相距20m,则甲楼的影子将落在乙楼上6m,若使甲楼的影子刚好不影响乙楼的采光,那么两楼的距离应是多少米?
39、某糖果厂为儿童设计一种新型的装糖果的不倒翁(如图5所示)
请你为包装厂设计出它的主视图、左视图和府视图.
40、画出图6中三棱柱的主视图、左视图、俯视图.
41、画出图7中空心圆柱的主视图、左视图、俯视图.
42、如图8所示,屋顶上有一只小猫,院子里有一只小老鼠,若小猫看见了小老鼠,则小老鼠就会有危险,试画出小老鼠在墙的左端的安全区.
拓广探索(共20分)
43、如图9为住宅区内的两幢楼,它们的高AB=CD=30m,两楼间的距离AC=30m,现需了解甲楼对乙楼的采光的影响情况,(1)当太阳光与水平线的夹角为30°角时,求甲楼的影子在乙楼上有多高(精确到0.1m,1.73);(2)若要甲楼的影子刚好不落在乙楼的墙上,此时太阳与水平线的夹角为多少度?
44、阳光通过窗口照到教室内,竖直窗框在地面上留下2.1m长的影子[如图(10)所示],已知窗框的影子DE到窗下墙脚的距离CE=3.9m,窗口底边离地面的距离BC=1.2m,试求窗口的高度(即AB的值)
45、一位同学想利用有关知识测旗杆的高度,他在某一时刻测得高为0.5m的小木棒的影长为0.3m,但当他马上测量旗杆的影长时,因旗杆靠近一幢建筑物,影子不全落在地面上,有一部分影子在墙上,他先测得留在墙上的影子CD=1.0m,又测地面部分的影长BC=3.0m,你能根据上述数据帮他测出旗杆的高度吗?
46、学习投影后,小明、小颖利用灯光下自己的影子长度来测量一路灯的高度,并探究影子长度的变化规律.如图7,在同一时间,身高为的小明的影子长是,而小颖刚好在路灯灯泡的正下方点,并测得.
(1)请在图中画出形成影子的光线,交确定路灯灯泡所在的位置;
(2)求路灯灯泡的垂直高度;
(3)如果小明沿线段向小颖(点)走去,当小明走到中点处时,求其影子的长;当小明继续走剩下路程的到处时,求其影子的长;当小明继续走剩下路程的到处,…按此规律继续走下去,当小明走剩下路程的到处时,其影子的长为
m(直接用的代数式表示).
【试题答案】
一、
1.
A
2.
A
3.
D
4.
A
5.
C
6.
C
7.
D
8、A;9、B;10、C;11、C;12、C;13、C;14、B;15、B;16、D;17、B;
二、
18.
阳光下
19
(1)不能
(2)能
20.
远离
21.
长,高度,距离
22
球
23
五棱柱
24、正方体或圆;25、平行投影,中心投影;26、减小盲区;27、14.6;28、圆锥;29、三角形,一条线段;30、长31、10;32、12;133、远;
三、
34.
解:过甲、乙建筑物顶端B、C两点作直线交地面于D,则汽车行至D点时刚好看不到甲建筑物,且∠BDE=45°。
在Rt△ACF中,
∠A=30°,CF=15
∴
在Rt△CFD中,
∵∠BDE=45°,∴∠FCD=45°
∴FD=CF=15
∴DA=AF-DF=。
答:他行驶了米。
35
36
(1)上图为路灯下的情形
下图为阳光下的情形
(2)上图先找到灯泡的位置再画树影
下图找出太阳光的方向,作平行线得到树影
37
乙比甲高
38.
由已知条件可求影长与物高的比为2,所以要使乙楼恰好采光不受影响,两楼的距离应为32m。
39、
40、
41、
42、略
43、(1)如图2,延长OB交DC于E,作EF⊥AB,交AB于F,
在Rt△BEF中,∵EF=AC=30m,∠FEB=30°,∴BE=2BF.
设BF=x,则
BE=2x.
根据勾股定理知
BE2=BF2+EF2
∴(2x)2=x2+302
∴(负值舍去),∴(m)
因此,EC=30-17.3=12.7(m)。
(2)当甲幢楼的影子刚好落在点C处时,△ABC为等腰三角形,因此,当太阳光与水平线夹角为45°时,甲楼的影子刚好不落在乙楼的墙上。
44、解:由于阳光是平行光线,即AE∥BD,
所以∠AEC=∠BDC.
又因为∠C是公共角,
所以△AEC∽△BDC,从而有.
又AC=AB+BC,DC=EC-ED,EC=3.9,ED=2.1,BC=1.2,
于是有,解得
AB=1.4(m)。
答:窗口的高度为1.4m。
45、能。旗杆的高度为6.0m。
分析:本题可以通过小明的身高和他的影子找出光源(即灯泡)的位置,由于路灯光线的投影是中心投影,然后利用相似三角形对应边成比例进行计算即可
46、解:(1)连接CA并延长交HE于G(如图3)
(2)由题意得:,
,,(m).
(3),,
图4
俯视图
主视图
左视图
图5
图6
图7
图8
图9
图10
图11
图2
图3
1
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
