高中数学人教A版(2019)必修第一册3.4新教材函数的应用(一)课件(共18张PPT)
文档属性
| 名称 | 高中数学人教A版(2019)必修第一册3.4新教材函数的应用(一)课件(共18张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-13 17:49:15 | ||
图片预览





文档简介
(共18张PPT)
3.4
函数的应用(一)
复习回顾:
1、常见的数学模型有哪些?
长春市地铁一号线的票价按照下列规则制定:
1、7km以内(含7km),票价2元;
2、每增加1元,可继续乘坐6、6、8、8、10km,
(不足6km的,按6km计算,以此类推)
如果地铁一号线的总里程为43km,请根据题意,写出票价与里程之间的函数解析式,并画出函数的图象。
模型初感知
前情提要:
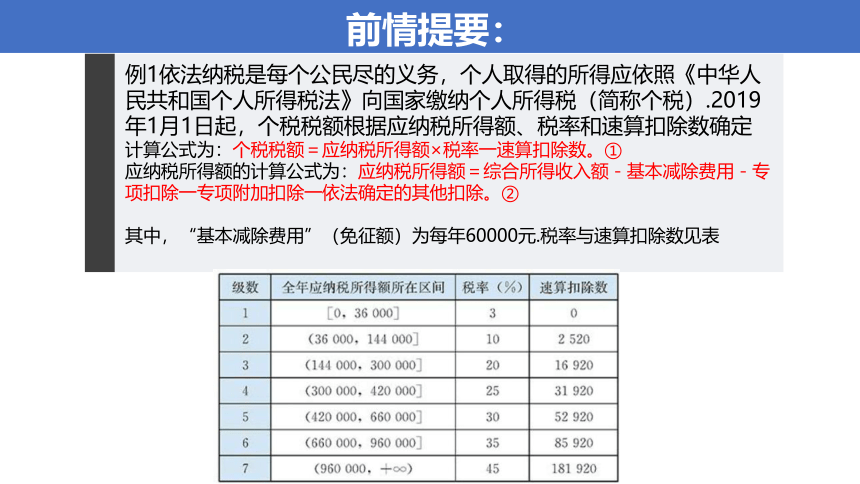
例1依法纳税是每个公民尽的义务,个人取得的所得应依照《中华人民共和国个人所得税法》向国家缴纳个人所得税(简称个税).2019年1月1日起,个税税额根据应纳税所得额、税率和速算扣除数确定
计算公式为:个税税额=应纳税所得额×税率一速算扣除数。①
应纳税所得额的计算公式为:应纳税所得额=综合所得收入额-基本减除费用-专项扣除一专项附加扣除一依法确定的其他扣除。②
其中,“基本减除费用”(免征额)为每年60000元.税率与速算扣除数见表
请在此处添加小标题
前情提要:
假定小王全年的综合所得收入额为189600元,“基本减除费用”(免征额)为每年60000元.假定缴纳的基本养老保险、基本医疗保险、失业保险等社会保险费和住房公积金占综合所得收入额的比例分别是8%,2%,1%,9%,专项附加扣除是52800元,依法确定其他扣除是4560元,那么他全年应缴纳多少综合所得个税?
应纳税所得额=综合所得收入额-基本减除费用-专项扣除
-专项附加扣除-依法确定的其他扣除。
将t的值代入,得
y=0.03×34320=1029.6
t=189600-60000-189600(8%+2%+1%
+9%)-52800-4560
=0.8×189600-117360
=34320.
前情提要:
模型深探究
假定小王缴纳的基本养老保险、基本医疗保险、失业保险等社会保险费和住房公积金占综合所得收入额的比例分别是8%,2%,1%,9%,专项附加扣除是52800元,依法确定其他扣除是4560元,全年综合所得收入额为x
(单位:元)
,那么他全年应缴纳综合所得个税为y(单位:元)
(1)求y关于x的函数解析式;
(2)如果小王全年的综合所得为249600元,那么他全年应缴纳多少综合所得个税?
探究1:本题中涉及了几个变量?你能写出它们之间的关系吗?
探究2:如何通过应纳税所得额t和全年综合所得
收入额x,确定应缴纳个税税额y与综合所
得收入额x之间的关系?
探究3:当x在什么范围内时可以使t落到相应的区间?
t=x-60000-x(8%+2%+1%+9%)-52800-4560=0.8x-117360
模型深探究
t
x
y
t=0
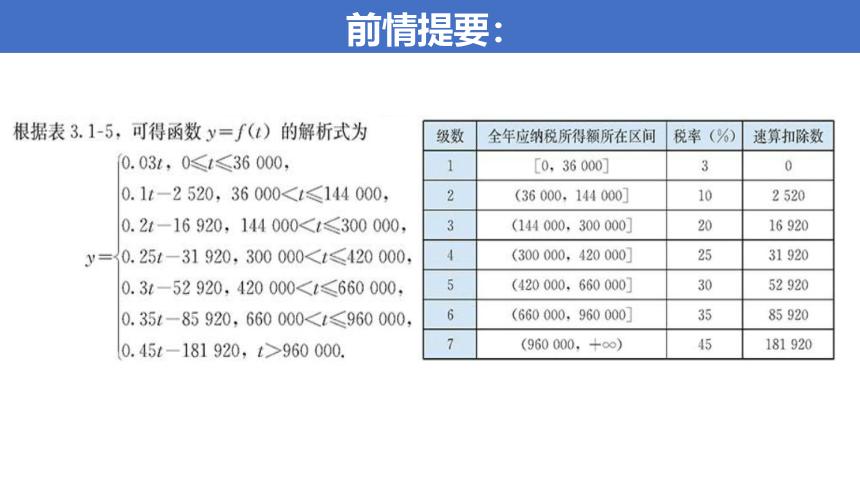
0<t≤36000
36000<t≤144000
144000<t≤300000
300000<t≤420000
420000<t≤660000
660000<t≤960000
t>960000
0≤x≤146700
y=0
146700<x≤191700
y=0.03t=0.024x-3520.8
191700<x≤326700
y=0.1t-2520=0.08x-14256
326700<x≤521700
y=0.2t-16920=0.16x-40392
521700<x≤671700
y=0.25t-31920=0.2x-61260
671700<x≤971700
y=0.3t-52920=0.24x-88128
971700<x≤1346700
y=0.35t-85920=0.28x-126996
x>1346700
y=0.45t-181920=0.36x-234732
模型深探究
模型深探究
模型实演练
例2一辆汽车在某段路程中行驶的平均速率v(单位:km/h)与时间t(单位:h)关系如图所示.
(1)求图中阴影部分的面积,并说明所求面积的实际含义;
解:
(1)阴影部分的面积为50×1+80×1+90×1+75×1+65×1=360.
阴影部分的面积表示
汽车在这5h内行驶的路程为360km.
探究1:
任取区间[0,5]内的一个时刻t0,
你能在图中画出对应的路程吗?
模型实演练
探究2:
我们知道汽车行驶路程l是关于时间t的函数,你能写出它的函数解析式吗?
当0≤t<1时,l=50t;
当1≤t<2时,l=80(t-1)+50;
当2≤t<3时,l=90(t-2)+130;
当3≤t<4时,l=75(t-3)+220;
当4≤t≤5时,l=65(t-4)+295.
模型实演练
例2一辆汽车在某段路程中行驶的平均速率v(单位:km/h)与时间t(单位:h)
关系如图所示.
(2)假设这辆汽车的里程表在汽车行驶这段路程前的读数
为2004km,试建立行驶这段路程时汽车里程表读数s(单位:km)
与时间t的函数解析式,并画出相应的图象.
探究3:你能根据上图画出汽车行驶路程关于时间变化的图象吗?为什么?
模型实演练
模型归纳
模型归纳
你能说说应用函数知识解决实际问题的一般步骤吗?
作业
巩固
数学精微何处寻,纷纭世界有模型。
描摹万象得神韵,识破玄机算古今。
岂是空闻无实效,能生妙策济苍生。
经天纬地展身手,七十二行任纵横。
3.4
函数的应用(一)
复习回顾:
1、常见的数学模型有哪些?
长春市地铁一号线的票价按照下列规则制定:
1、7km以内(含7km),票价2元;
2、每增加1元,可继续乘坐6、6、8、8、10km,
(不足6km的,按6km计算,以此类推)
如果地铁一号线的总里程为43km,请根据题意,写出票价与里程之间的函数解析式,并画出函数的图象。
模型初感知
前情提要:
例1依法纳税是每个公民尽的义务,个人取得的所得应依照《中华人民共和国个人所得税法》向国家缴纳个人所得税(简称个税).2019年1月1日起,个税税额根据应纳税所得额、税率和速算扣除数确定
计算公式为:个税税额=应纳税所得额×税率一速算扣除数。①
应纳税所得额的计算公式为:应纳税所得额=综合所得收入额-基本减除费用-专项扣除一专项附加扣除一依法确定的其他扣除。②
其中,“基本减除费用”(免征额)为每年60000元.税率与速算扣除数见表
请在此处添加小标题
前情提要:
假定小王全年的综合所得收入额为189600元,“基本减除费用”(免征额)为每年60000元.假定缴纳的基本养老保险、基本医疗保险、失业保险等社会保险费和住房公积金占综合所得收入额的比例分别是8%,2%,1%,9%,专项附加扣除是52800元,依法确定其他扣除是4560元,那么他全年应缴纳多少综合所得个税?
应纳税所得额=综合所得收入额-基本减除费用-专项扣除
-专项附加扣除-依法确定的其他扣除。
将t的值代入,得
y=0.03×34320=1029.6
t=189600-60000-189600(8%+2%+1%
+9%)-52800-4560
=0.8×189600-117360
=34320.
前情提要:
模型深探究
假定小王缴纳的基本养老保险、基本医疗保险、失业保险等社会保险费和住房公积金占综合所得收入额的比例分别是8%,2%,1%,9%,专项附加扣除是52800元,依法确定其他扣除是4560元,全年综合所得收入额为x
(单位:元)
,那么他全年应缴纳综合所得个税为y(单位:元)
(1)求y关于x的函数解析式;
(2)如果小王全年的综合所得为249600元,那么他全年应缴纳多少综合所得个税?
探究1:本题中涉及了几个变量?你能写出它们之间的关系吗?
探究2:如何通过应纳税所得额t和全年综合所得
收入额x,确定应缴纳个税税额y与综合所
得收入额x之间的关系?
探究3:当x在什么范围内时可以使t落到相应的区间?
t=x-60000-x(8%+2%+1%+9%)-52800-4560=0.8x-117360
模型深探究
t
x
y
t=0
0<t≤36000
36000<t≤144000
144000<t≤300000
300000<t≤420000
420000<t≤660000
660000<t≤960000
t>960000
0≤x≤146700
y=0
146700<x≤191700
y=0.03t=0.024x-3520.8
191700<x≤326700
y=0.1t-2520=0.08x-14256
326700<x≤521700
y=0.2t-16920=0.16x-40392
521700<x≤671700
y=0.25t-31920=0.2x-61260
671700<x≤971700
y=0.3t-52920=0.24x-88128
971700<x≤1346700
y=0.35t-85920=0.28x-126996
x>1346700
y=0.45t-181920=0.36x-234732
模型深探究
模型深探究
模型实演练
例2一辆汽车在某段路程中行驶的平均速率v(单位:km/h)与时间t(单位:h)关系如图所示.
(1)求图中阴影部分的面积,并说明所求面积的实际含义;
解:
(1)阴影部分的面积为50×1+80×1+90×1+75×1+65×1=360.
阴影部分的面积表示
汽车在这5h内行驶的路程为360km.
探究1:
任取区间[0,5]内的一个时刻t0,
你能在图中画出对应的路程吗?
模型实演练
探究2:
我们知道汽车行驶路程l是关于时间t的函数,你能写出它的函数解析式吗?
当0≤t<1时,l=50t;
当1≤t<2时,l=80(t-1)+50;
当2≤t<3时,l=90(t-2)+130;
当3≤t<4时,l=75(t-3)+220;
当4≤t≤5时,l=65(t-4)+295.
模型实演练
例2一辆汽车在某段路程中行驶的平均速率v(单位:km/h)与时间t(单位:h)
关系如图所示.
(2)假设这辆汽车的里程表在汽车行驶这段路程前的读数
为2004km,试建立行驶这段路程时汽车里程表读数s(单位:km)
与时间t的函数解析式,并画出相应的图象.
探究3:你能根据上图画出汽车行驶路程关于时间变化的图象吗?为什么?
模型实演练
模型归纳
模型归纳
你能说说应用函数知识解决实际问题的一般步骤吗?
作业
巩固
数学精微何处寻,纷纭世界有模型。
描摹万象得神韵,识破玄机算古今。
岂是空闻无实效,能生妙策济苍生。
经天纬地展身手,七十二行任纵横。
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
