人教版九年级上册:24.3正多边形和圆同步练习卷 Word版含答案
文档属性
| 名称 | 人教版九年级上册:24.3正多边形和圆同步练习卷 Word版含答案 |
|
|
| 格式 | zip | ||
| 文件大小 | 212.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-13 00:00:00 | ||
图片预览


文档简介
人教版九年级上册:24.3《正多边形和圆》同步练习卷
一.选择题
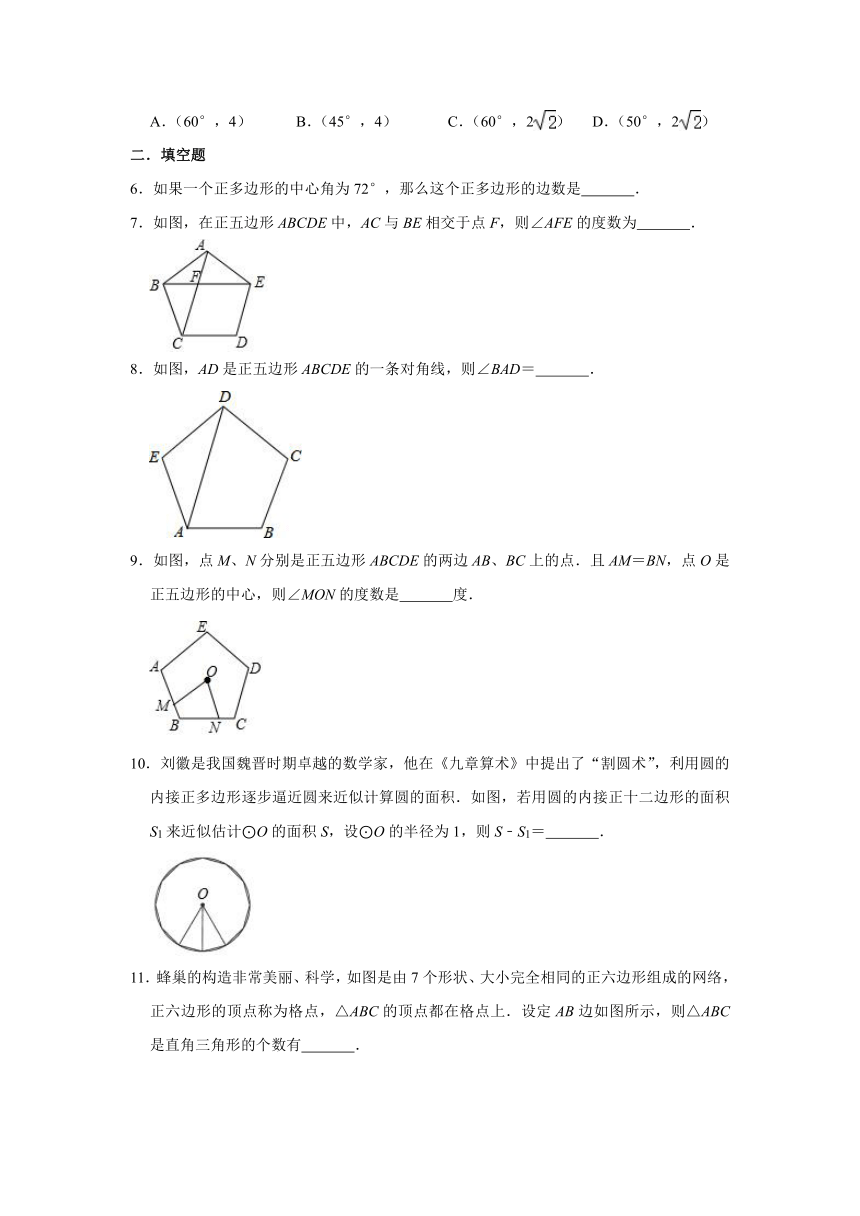
1.如图,已知⊙O的内接正方形边长为2,则⊙O的半径是( )
A.1
B.2
C.
D.
2.若正六边形外接圆的半径为4,则它的边长为( )
A.2
B.
C.4
D.
3.正六边形内接于圆,它的边所对的圆周角是( )
A.60°
B.120°
C.60°或120°
D.30°或150°
4.如图,正五边形ABCDE内接于⊙O,P为上的一点(点P不与点D重合),则∠CPD的度数为( )
A.30°
B.36°
C.60°
D.72°
5.阅读理解:如图1,在平面内选一定点O,引一条有方向的射线Ox,再选定一个单位长度,那么平面上任一点M的位置可由∠MOx的度数θ与OM的长度m确定,有序数对(θ,m)称为M点的“极坐标”,这样建立的坐标系称为“极坐标系”.
应用:在图2的极坐标系下,如果正六边形的边长为2,有一边OA在射线Ox上,则正六边形的顶点C的极坐标应记为( )
A.(60°,4)
B.(45°,4)
C.(60°,2)
D.(50°,2)
二.填空题
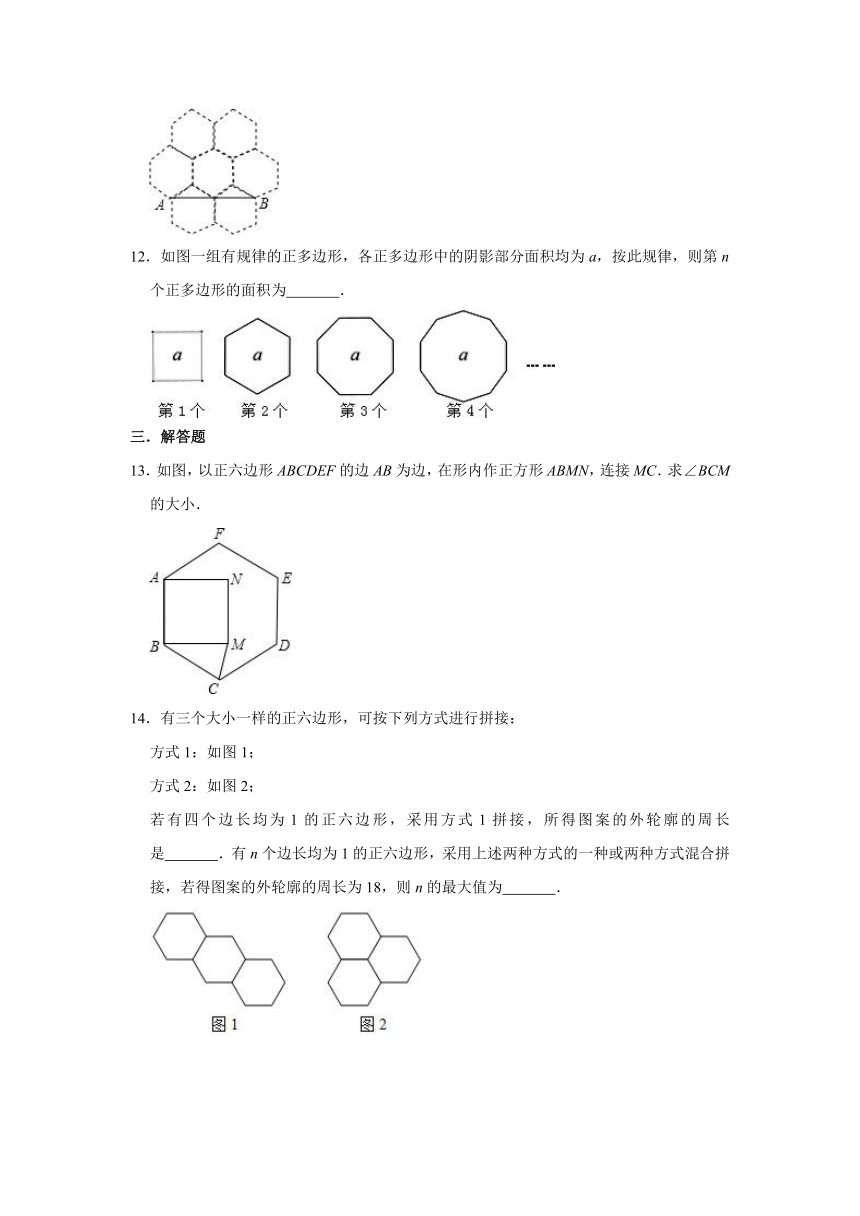
6.如果一个正多边形的中心角为72°,那么这个正多边形的边数是
.
7.如图,在正五边形ABCDE中,AC与BE相交于点F,则∠AFE的度数为
.
8.如图,AD是正五边形ABCDE的一条对角线,则∠BAD=
.
9.如图,点M、N分别是正五边形ABCDE的两边AB、BC上的点.且AM=BN,点O是正五边形的中心,则∠MON的度数是
度.
10.刘徽是我国魏晋时期卓越的数学家,他在《九章算术》中提出了“割圆术”,利用圆的内接正多边形逐步逼近圆来近似计算圆的面积.如图,若用圆的内接正十二边形的面积S1来近似估计⊙O的面积S,设⊙O的半径为1,则S﹣S1=
.
11.蜂巢的构造非常美丽、科学,如图是由7个形状、大小完全相同的正六边形组成的网络,正六边形的顶点称为格点,△ABC的顶点都在格点上.设定AB边如图所示,则△ABC是直角三角形的个数有
.
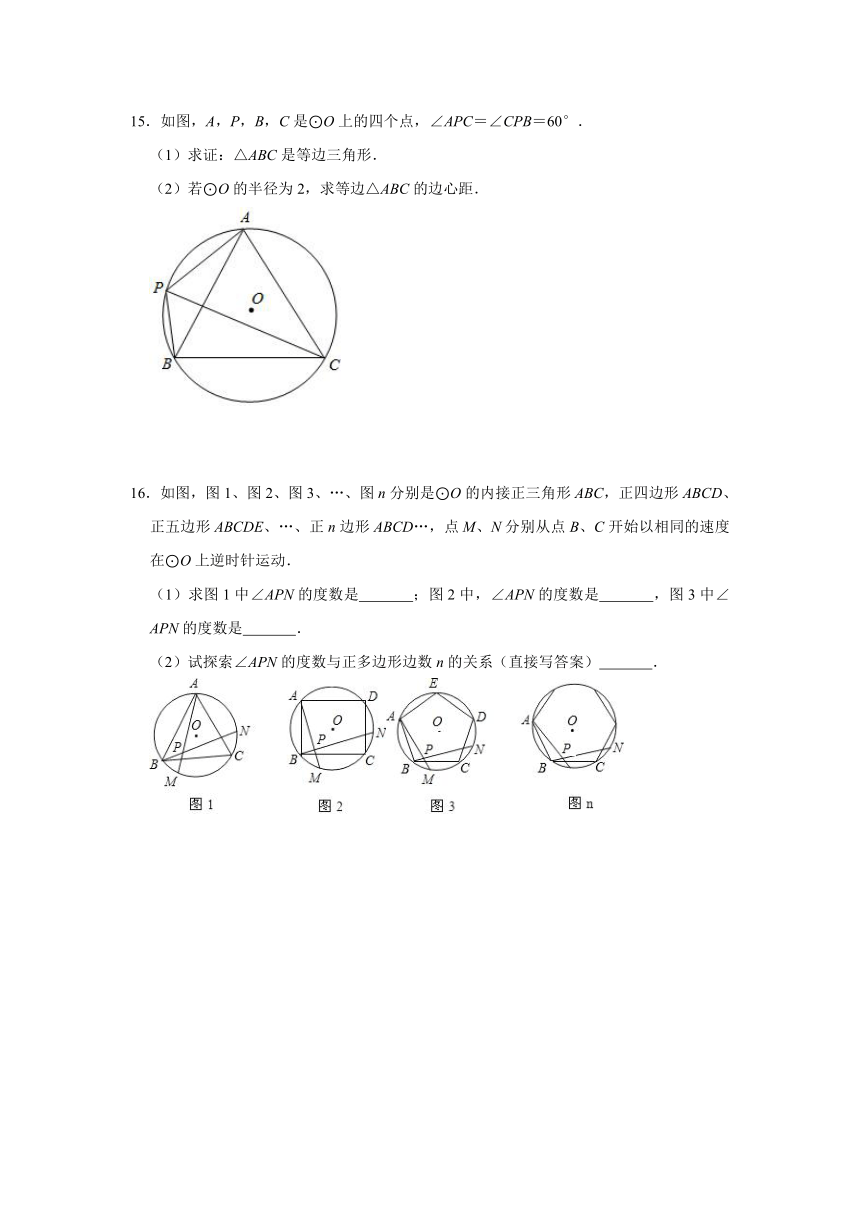
12.如图一组有规律的正多边形,各正多边形中的阴影部分面积均为a,按此规律,则第n个正多边形的面积为
.
三.解答题
13.如图,以正六边形ABCDEF的边AB为边,在形内作正方形ABMN,连接MC.求∠BCM的大小.
14.有三个大小一样的正六边形,可按下列方式进行拼接:
方式1:如图1;
方式2:如图2;
若有四个边长均为1的正六边形,采用方式1拼接,所得图案的外轮廓的周长是
.有n个边长均为1的正六边形,采用上述两种方式的一种或两种方式混合拼接,若得图案的外轮廓的周长为18,则n的最大值为
.
15.如图,A,P,B,C是⊙O上的四个点,∠APC=∠CPB=60°.
(1)求证:△ABC是等边三角形.
(2)若⊙O的半径为2,求等边△ABC的边心距.
16.如图,图1、图2、图3、…、图n分别是⊙O的内接正三角形ABC,正四边形ABCD、正五边形ABCDE、…、正n边形ABCD…,点M、N分别从点B、C开始以相同的速度在⊙O上逆时针运动.
(1)求图1中∠APN的度数是
;图2中,∠APN的度数是
,图3中∠APN的度数是
.
(2)试探索∠APN的度数与正多边形边数n的关系(直接写答案)
.
参考答案
一.选择题
1.解:如图所示,
∵四边形ABCD是正方形,∠B=90°,
∴AC是⊙O的直径,
∵AB2+BC2=AC2,AB=BC,
∴AB2+BC2=22+22=8,
∴AC=2,
∴⊙O的半径是,
故选:C.
2.解:正六边形的中心角为360°÷6=60°,那么外接圆的半径和正六边形的边长将组成一个等边三角形,
故正六边形的外接圆半径等于4,则正六边形的边长是4.
故选:C.
3.解:圆内接正六边形的边所对的圆心角=360°÷6=60°,
根据圆周角等于同弧所对圆心角的一半,
边所对的圆周角的度数是60×=30°或180°﹣30°=150°.
故选:D.
4.解:如图,连接OC,OD.
∵ABCDE是正五边形,
∴∠COD==72°,
∴∠CPD=∠COD=36°,
故选:B.
5.解:如图,设正六边形的中心为D,连接AD,
∵∠ADO=360°÷6=60°,OD=AD,
∴△AOD是等边三角形,
∴OD=OA=2,∠AOD=60°,
∴OC=2OD=2×2=4,
∴正六边形的顶点C的极坐标应记为(60°,4).
故选:A.
二.填空题
6.解:根据题意得:
这个多边形的边数是360°÷72°=5,
故答案为:5.
7.解:∵五边形ABCDE是正五边形,
∴∠EAB=∠ABC==108°,
∵BA=BC,
∴∠BAC=∠BCA=36°,
同理∠ABE=36°,
∴∠AFE=∠ABF+∠BAF=36°+36°=72°,
故答案为:72°.
8.解:∵正五边形ABCDE的内角和为(5﹣2)×180°=540°,
∴∠E=×540°=108°,∠BAE=108°
又∵EA=ED,
∴∠EAD=×(180°﹣108°)=36°,
∴∠BAD=∠BAE﹣∠EAD=72°,
故答案是:72°.
9.解:连接OA、OB、OC,
∠AOB==72°,
∵∠AOB=∠BOC,OA=OB,OB=OC,
∴∠OAB=∠OBC,
在△AOM和△BON中,
∴△AOM≌△BON,
∴∠BON=∠AOM,
∴∠MON=∠AOB=72°,
故答案为:72.
10.解:∵⊙O的半径为1,
∴⊙O的面积S=π,
∴圆的内接正十二边形的中心角为=30°,
∴过A作AC⊥OB,
∴AC=OA=,
∴圆的内接正十二边形的面积S1=12××1×=3,
∴则S﹣S1=π﹣3,
故答案为:π﹣3.
11.解:如图,AB是直角边时,点C共有6个位置,即有6个直角三角形,
AB是斜边时,点C共有4个位置,即有4个直角三角形,
综上所述,△ABC是直角三角形的个数有6+4=10个.
故答案为:10.
12.解:第一个:正多边形的面积等于a;
第二个:如图作AE⊥BD于E,
设正六边形的边长为2,
∵正六边形的一个内角为120°,
∴∠ABE=30°,
则AE=1,BE=,
△ABD的面积为:×2×1=,
a=2×2=4,
∴正六边形的面积为:a,
第三个:如图,
∵正八边形的一个内角为135°,
∴∠ABD=45°,
设正八边形的边长为2,
则BD=AD=,△ABD的面积为1,
四边形ABEF的面积为1+2+1=2+2,
a=2×(2+2)=4+4,
∴正八边形的面积为2a,
通过计算可以看出:第n个正多边形的面积为a.
三.解答题
13.解:∵六边形ABCDEF为正六边形,
∴∠ABC=120°,AB=BC.
∵四边形ABMN为正方形,
∴∠ABM=90°,AB=BM.(2分)
∴∠MBC=120°﹣90°=30°,BM=BC.
∴∠BCM=∠BMC.
∴∠BCM=×(180°﹣30°)=75°.(5分)
14.解:有四个边长均为1的正六边形,采用方式1拼接,所得图案的外轮廓的周长为4×4+2=18;
按下图拼接,图案的外轮廓的周长为18,此时正六边形的个数最多,即n的最大值为7.
故答案为:18,7.
15.(1)证明:在⊙O中,
∵∠BAC与∠CPB是对的圆周角,∠ABC与∠APC是所对的圆周角,
∴∠BAC=∠CPB,∠ABC=∠APC,
又∵∠APC=∠CPB=60°,
∴∠ABC=∠BAC=60°,
∴△ABC为等边三角形;
(2)过O作OD⊥BC于D,连接OB,
则∠OBD=30°,∠ODB=90°,
∵OB=2,
∴OD=1,
∴等边△ABC的边心距为1.
16.解:(1)图1:∵点M、N分别从点B、C开始以相同的速度在⊙O上逆时针运动,
∴∠BAM=∠CBN,
又∵∠APN=∠BPM,
∴∠APN=∠BPM=∠ABN+∠BAM=∠ABN+∠CBN=∠ABC=60°;
同理可得:在图2中,∠APN=90°;在图3中,∠APN=108°.
(2)由(1)可知,∠APN=所在多边形的内角度数,故在图n中,.
一.选择题
1.如图,已知⊙O的内接正方形边长为2,则⊙O的半径是( )
A.1
B.2
C.
D.
2.若正六边形外接圆的半径为4,则它的边长为( )
A.2
B.
C.4
D.
3.正六边形内接于圆,它的边所对的圆周角是( )
A.60°
B.120°
C.60°或120°
D.30°或150°
4.如图,正五边形ABCDE内接于⊙O,P为上的一点(点P不与点D重合),则∠CPD的度数为( )
A.30°
B.36°
C.60°
D.72°
5.阅读理解:如图1,在平面内选一定点O,引一条有方向的射线Ox,再选定一个单位长度,那么平面上任一点M的位置可由∠MOx的度数θ与OM的长度m确定,有序数对(θ,m)称为M点的“极坐标”,这样建立的坐标系称为“极坐标系”.
应用:在图2的极坐标系下,如果正六边形的边长为2,有一边OA在射线Ox上,则正六边形的顶点C的极坐标应记为( )
A.(60°,4)
B.(45°,4)
C.(60°,2)
D.(50°,2)
二.填空题
6.如果一个正多边形的中心角为72°,那么这个正多边形的边数是
.
7.如图,在正五边形ABCDE中,AC与BE相交于点F,则∠AFE的度数为
.
8.如图,AD是正五边形ABCDE的一条对角线,则∠BAD=
.
9.如图,点M、N分别是正五边形ABCDE的两边AB、BC上的点.且AM=BN,点O是正五边形的中心,则∠MON的度数是
度.
10.刘徽是我国魏晋时期卓越的数学家,他在《九章算术》中提出了“割圆术”,利用圆的内接正多边形逐步逼近圆来近似计算圆的面积.如图,若用圆的内接正十二边形的面积S1来近似估计⊙O的面积S,设⊙O的半径为1,则S﹣S1=
.
11.蜂巢的构造非常美丽、科学,如图是由7个形状、大小完全相同的正六边形组成的网络,正六边形的顶点称为格点,△ABC的顶点都在格点上.设定AB边如图所示,则△ABC是直角三角形的个数有
.
12.如图一组有规律的正多边形,各正多边形中的阴影部分面积均为a,按此规律,则第n个正多边形的面积为
.
三.解答题
13.如图,以正六边形ABCDEF的边AB为边,在形内作正方形ABMN,连接MC.求∠BCM的大小.
14.有三个大小一样的正六边形,可按下列方式进行拼接:
方式1:如图1;
方式2:如图2;
若有四个边长均为1的正六边形,采用方式1拼接,所得图案的外轮廓的周长是
.有n个边长均为1的正六边形,采用上述两种方式的一种或两种方式混合拼接,若得图案的外轮廓的周长为18,则n的最大值为
.
15.如图,A,P,B,C是⊙O上的四个点,∠APC=∠CPB=60°.
(1)求证:△ABC是等边三角形.
(2)若⊙O的半径为2,求等边△ABC的边心距.
16.如图,图1、图2、图3、…、图n分别是⊙O的内接正三角形ABC,正四边形ABCD、正五边形ABCDE、…、正n边形ABCD…,点M、N分别从点B、C开始以相同的速度在⊙O上逆时针运动.
(1)求图1中∠APN的度数是
;图2中,∠APN的度数是
,图3中∠APN的度数是
.
(2)试探索∠APN的度数与正多边形边数n的关系(直接写答案)
.
参考答案
一.选择题
1.解:如图所示,
∵四边形ABCD是正方形,∠B=90°,
∴AC是⊙O的直径,
∵AB2+BC2=AC2,AB=BC,
∴AB2+BC2=22+22=8,
∴AC=2,
∴⊙O的半径是,
故选:C.
2.解:正六边形的中心角为360°÷6=60°,那么外接圆的半径和正六边形的边长将组成一个等边三角形,
故正六边形的外接圆半径等于4,则正六边形的边长是4.
故选:C.
3.解:圆内接正六边形的边所对的圆心角=360°÷6=60°,
根据圆周角等于同弧所对圆心角的一半,
边所对的圆周角的度数是60×=30°或180°﹣30°=150°.
故选:D.
4.解:如图,连接OC,OD.
∵ABCDE是正五边形,
∴∠COD==72°,
∴∠CPD=∠COD=36°,
故选:B.
5.解:如图,设正六边形的中心为D,连接AD,
∵∠ADO=360°÷6=60°,OD=AD,
∴△AOD是等边三角形,
∴OD=OA=2,∠AOD=60°,
∴OC=2OD=2×2=4,
∴正六边形的顶点C的极坐标应记为(60°,4).
故选:A.
二.填空题
6.解:根据题意得:
这个多边形的边数是360°÷72°=5,
故答案为:5.
7.解:∵五边形ABCDE是正五边形,
∴∠EAB=∠ABC==108°,
∵BA=BC,
∴∠BAC=∠BCA=36°,
同理∠ABE=36°,
∴∠AFE=∠ABF+∠BAF=36°+36°=72°,
故答案为:72°.
8.解:∵正五边形ABCDE的内角和为(5﹣2)×180°=540°,
∴∠E=×540°=108°,∠BAE=108°
又∵EA=ED,
∴∠EAD=×(180°﹣108°)=36°,
∴∠BAD=∠BAE﹣∠EAD=72°,
故答案是:72°.
9.解:连接OA、OB、OC,
∠AOB==72°,
∵∠AOB=∠BOC,OA=OB,OB=OC,
∴∠OAB=∠OBC,
在△AOM和△BON中,
∴△AOM≌△BON,
∴∠BON=∠AOM,
∴∠MON=∠AOB=72°,
故答案为:72.
10.解:∵⊙O的半径为1,
∴⊙O的面积S=π,
∴圆的内接正十二边形的中心角为=30°,
∴过A作AC⊥OB,
∴AC=OA=,
∴圆的内接正十二边形的面积S1=12××1×=3,
∴则S﹣S1=π﹣3,
故答案为:π﹣3.
11.解:如图,AB是直角边时,点C共有6个位置,即有6个直角三角形,
AB是斜边时,点C共有4个位置,即有4个直角三角形,
综上所述,△ABC是直角三角形的个数有6+4=10个.
故答案为:10.
12.解:第一个:正多边形的面积等于a;
第二个:如图作AE⊥BD于E,
设正六边形的边长为2,
∵正六边形的一个内角为120°,
∴∠ABE=30°,
则AE=1,BE=,
△ABD的面积为:×2×1=,
a=2×2=4,
∴正六边形的面积为:a,
第三个:如图,
∵正八边形的一个内角为135°,
∴∠ABD=45°,
设正八边形的边长为2,
则BD=AD=,△ABD的面积为1,
四边形ABEF的面积为1+2+1=2+2,
a=2×(2+2)=4+4,
∴正八边形的面积为2a,
通过计算可以看出:第n个正多边形的面积为a.
三.解答题
13.解:∵六边形ABCDEF为正六边形,
∴∠ABC=120°,AB=BC.
∵四边形ABMN为正方形,
∴∠ABM=90°,AB=BM.(2分)
∴∠MBC=120°﹣90°=30°,BM=BC.
∴∠BCM=∠BMC.
∴∠BCM=×(180°﹣30°)=75°.(5分)
14.解:有四个边长均为1的正六边形,采用方式1拼接,所得图案的外轮廓的周长为4×4+2=18;
按下图拼接,图案的外轮廓的周长为18,此时正六边形的个数最多,即n的最大值为7.
故答案为:18,7.
15.(1)证明:在⊙O中,
∵∠BAC与∠CPB是对的圆周角,∠ABC与∠APC是所对的圆周角,
∴∠BAC=∠CPB,∠ABC=∠APC,
又∵∠APC=∠CPB=60°,
∴∠ABC=∠BAC=60°,
∴△ABC为等边三角形;
(2)过O作OD⊥BC于D,连接OB,
则∠OBD=30°,∠ODB=90°,
∵OB=2,
∴OD=1,
∴等边△ABC的边心距为1.
16.解:(1)图1:∵点M、N分别从点B、C开始以相同的速度在⊙O上逆时针运动,
∴∠BAM=∠CBN,
又∵∠APN=∠BPM,
∴∠APN=∠BPM=∠ABN+∠BAM=∠ABN+∠CBN=∠ABC=60°;
同理可得:在图2中,∠APN=90°;在图3中,∠APN=108°.
(2)由(1)可知,∠APN=所在多边形的内角度数,故在图n中,.
同课章节目录
