21.4 第1课时 二次函数的应用中的面积、利润最值问题 课件(共21张PPT)
文档属性
| 名称 | 21.4 第1课时 二次函数的应用中的面积、利润最值问题 课件(共21张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-15 09:15:21 | ||
图片预览






文档简介
(共21张PPT)
21.4
二次函数的应用
第1课时
二次函数的应用中的面积、利润最值问题
沪科版
九年级数学上册
上课课件
学习目标
【知识与技能】
经历探究图形的最大面积问题的过程,进一步获得利用数学方法解决实际问题的经验.
【过程与方法】
经历探索问题的过程,获得利用数学方法解决实际问题的经验,感受数学模型和数学应用的价值,通过观察、比较、推理、交流等过程,发展获得一些研究问题与合作交流的方法与经验.
【情感态度】
通过动手实做及同学之间的合作与交流,让学生积累经验,发展学习动力.
【教学重点】
会根据不同的条件,利用二次函数解决生活中的实际问题.
【教学难点】
从几何背景及实际情景中抽象出函数模型.
新课导入
某水产养殖户用长40m的围网,在水库中围一块矩形的水面,投放鱼苗.要使围成的水面面积最大,则它的边长应是多少米?
解:设围成的矩形水面的一边长为xm,那么,矩形水面的另一边长应为(20-x)m.若它的面积是Sm2,则有
S=x(20-x)
将这个函数的表达式配方,得
S=-
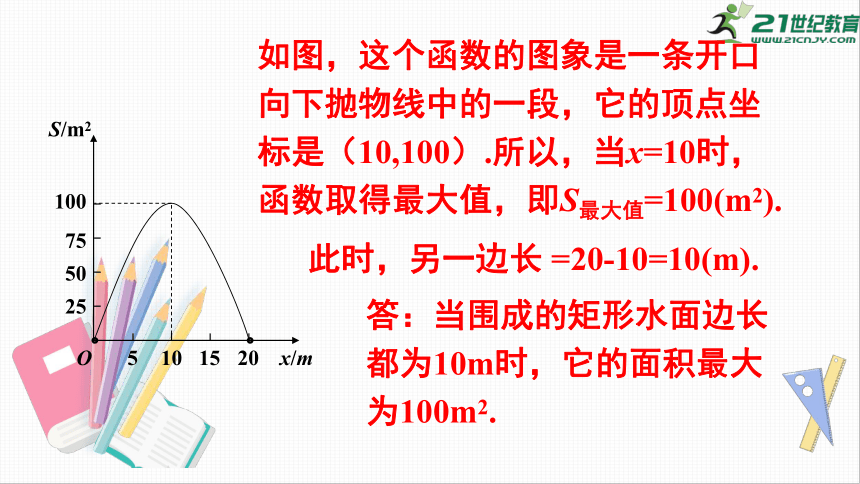
(x-10)2+100(025
O
5
10
15
20
x/m
50
75
100
S/m2
如图,这个函数的图象是一条开口向下抛物线中的一段,它的顶点坐标是(10,100).所以,当x=10时,函数取得最大值,即S最大值=100(m2).
此时,另一边长
=20-10=10(m).
答:当围成的矩形水面边长都为10m时,它的面积最大为100m2.
利用二次函数解决几何图形中的最值问题的要点:
1.根据面积公式、周长公式、勾股定理等建立函数关系式;
2.确定自变量的取值范围;
3.根据开口方向、顶点坐标和自变量的取值范围画草图;
4.根据草图求所得函数在自变量的允许范围内的最大值或最小值.
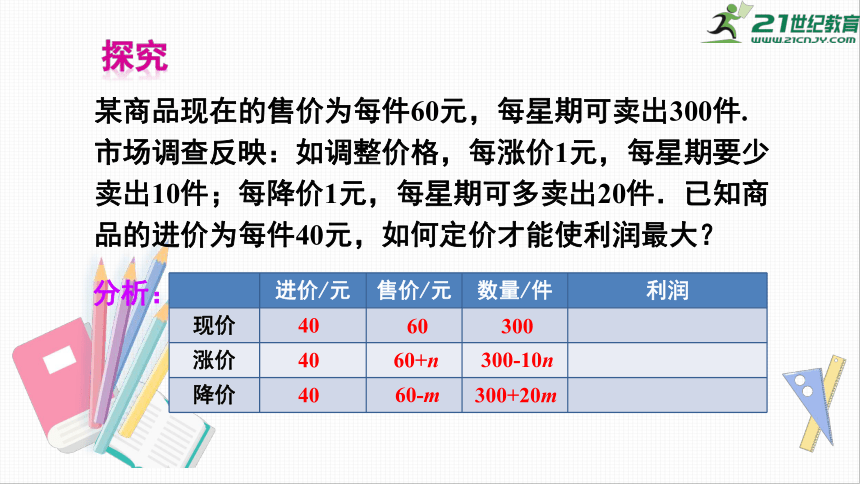
某商品现在的售价为每件60元,每星期可卖出300件.市场调查反映:如调整价格,每涨价1元,每星期要少卖出10件;每降价1元,每星期可多卖出20件.已知商品的进价为每件40元,如何定价才能使利润最大?
探究
进价/元
售价/元
数量/件
利润
现价
涨价
降价
分析:
40
60
300
60+n
300-10n
60-m
300+20m
40
40
进价/元
售价/元
销量/件
利润
现价
涨价
降价
40
60
300
60+n
300-10n
60-m
300+20m
40
40
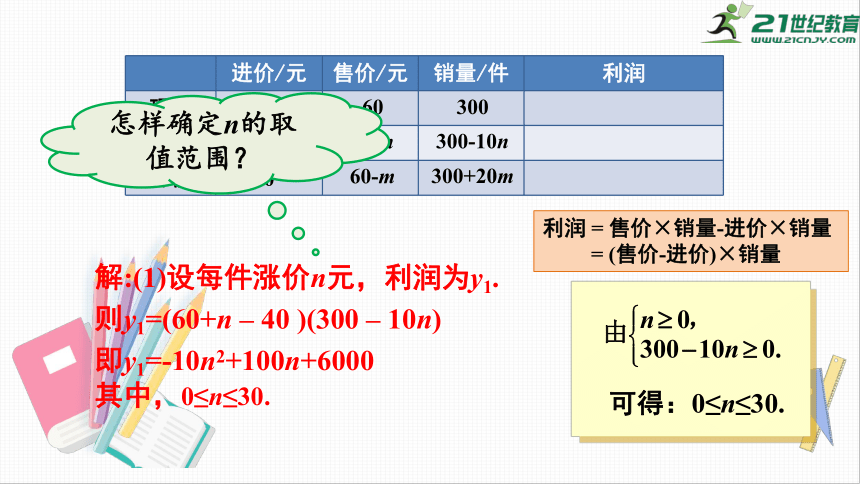
解:(1)设每件涨价n元,利润为y1.
则y1=(60+n
–
40
)(300
–
10n)
即y1=-10n2+100n+6000
其中,0≤n≤30.
利润
=
售价×销量-进价×销量
=
(售价-进价)×销量
怎样确定n的取值范围?
可得:0≤n≤30.
y1=-10n2+100n+6000
(0≤n≤30)
抛物线y1
=-10n2+100n+6000顶点坐标为
,所以商品的单价上涨
元时,利润最大,为
元.
(5,6250)
5
6250
n取何值时,y有最大值?最大值是多少?
=-10(n2-10n)+6000
=-10(n-5)2+6250
即涨价情况下,定价65元时,有最大利润6250元.
涨价:
进价/元
售价/元
销量/件
利润
降价
40
60-m
300+20m
解:
(2)设每件降价m元,利润为y2.
则y2=(60-m
–
40
)(300
+20m)
即y2=-20m2+100m+6000
其中,0≤m≤20.
怎样确定m的取值范围?
可得:0≤m≤20.
降价情况下的最大利润又是多少呢?
y2=-20m2+100m+6000
(0≤m≤20)
抛物线y2=-20m2+100m+6000顶点坐标为
,所以商品的单价下降
元时,利润最大,为
元.
(2.5,6125)
2.5
6125
m取何值时,y有最大值?最大值是多少?
即降价情况下,定价57.5元时,有最大利润6125元.
降价:
=-20(m2-5m)+6000
=-20(m-2.5)2+6125
(2)降价情况下,定价57.5元时,有最大利润6125元.
(1)涨价情况下,定价65元时,有最大利润6250元.
综上可知:
该商品的价格定价为65元时,可获得最大利润6250元.
随堂练习
1.如图,四边形的两条对角线AC、BD互相垂直,AC+
BD=10,当AC、BD的长是多少时,四边形ABCD的面
积最大?
解:设AC=x,四边形ABCD面积为y,
则BD=(10-x).
即当AC、BD的长均为5时,四边形ABCD的面积最大.
2.用一段长为30m的篱笆围成一个一边靠墙的矩形菜园(如图所示),墙长为18m,这个矩形的长,宽各为多少时,菜园的面积最大,最大面积是多少?
解:设矩形的长为x
m,面积为y
m2,则矩形的宽为
m.
∴03.已知矩形的周长为36cm,矩形绕它的一条边旋转形成一个圆柱,矩形的长、宽各为多少时,圆柱的侧面积最大?
解:设矩形的长为xcm,圆柱的侧面积为ycm2,
则矩形的宽为(18-x)cm,绕矩形的长或宽旋转,圆柱的侧面积相等.
有y=2πx(18-x)=-2π(x-9)2+162π(0<x<18).
当x=9时,y有最大值为162π.
即当矩形的长、宽各为9cm时,圆柱的侧面积最大。
4.某种商品每件的进价为30元,在某段时间内若以每件x元出售,可卖出(200-x)件,应如何定价才能使利润最大?
解:设所得利润为y元,
由题意得y=x(200-x)-30(200-x)
=-x2+230x-6000
=-(x-115)2+7225
(0当x=115时,y有最大值.
即当这件商品定价为115元时,利润最大.
5.某种文化衫以每件盈利20元的价格出售,每天可售出40件.
若每件降价1元,则每天可多售10件,如果每天要盈利最多,每件应降价多少元?
解:设每件应降价x元,每天的利润为y元,
由题意得:y=(20-x)(40+10x)
=-10x2+160x+800
=-10(x-8)2+1440
(0<x<20).
当x=8时,y取最大值1440.
即当每件降价8元时,每天的盈利最多。
课堂小结
图形面积最值问题:
由图形面积公式直接计算列出关系式,再利用二次函数的性质分析、解决问题.
利用二次函数解决利润问题的一般步骤:
①审清题意,理解问题;②分析问题中的变量和常量以及数量之间的关系;③列出函数关系式;④求解数学问题;⑤求解实际问题.
课后作业
1.完成课本课后习题;
2.完成练习册本课时的习题。
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
21.4
二次函数的应用
第1课时
二次函数的应用中的面积、利润最值问题
沪科版
九年级数学上册
上课课件
学习目标
【知识与技能】
经历探究图形的最大面积问题的过程,进一步获得利用数学方法解决实际问题的经验.
【过程与方法】
经历探索问题的过程,获得利用数学方法解决实际问题的经验,感受数学模型和数学应用的价值,通过观察、比较、推理、交流等过程,发展获得一些研究问题与合作交流的方法与经验.
【情感态度】
通过动手实做及同学之间的合作与交流,让学生积累经验,发展学习动力.
【教学重点】
会根据不同的条件,利用二次函数解决生活中的实际问题.
【教学难点】
从几何背景及实际情景中抽象出函数模型.
新课导入
某水产养殖户用长40m的围网,在水库中围一块矩形的水面,投放鱼苗.要使围成的水面面积最大,则它的边长应是多少米?
解:设围成的矩形水面的一边长为xm,那么,矩形水面的另一边长应为(20-x)m.若它的面积是Sm2,则有
S=x(20-x)
将这个函数的表达式配方,得
S=-
(x-10)2+100(0
O
5
10
15
20
x/m
50
75
100
S/m2
如图,这个函数的图象是一条开口向下抛物线中的一段,它的顶点坐标是(10,100).所以,当x=10时,函数取得最大值,即S最大值=100(m2).
此时,另一边长
=20-10=10(m).
答:当围成的矩形水面边长都为10m时,它的面积最大为100m2.
利用二次函数解决几何图形中的最值问题的要点:
1.根据面积公式、周长公式、勾股定理等建立函数关系式;
2.确定自变量的取值范围;
3.根据开口方向、顶点坐标和自变量的取值范围画草图;
4.根据草图求所得函数在自变量的允许范围内的最大值或最小值.
某商品现在的售价为每件60元,每星期可卖出300件.市场调查反映:如调整价格,每涨价1元,每星期要少卖出10件;每降价1元,每星期可多卖出20件.已知商品的进价为每件40元,如何定价才能使利润最大?
探究
进价/元
售价/元
数量/件
利润
现价
涨价
降价
分析:
40
60
300
60+n
300-10n
60-m
300+20m
40
40
进价/元
售价/元
销量/件
利润
现价
涨价
降价
40
60
300
60+n
300-10n
60-m
300+20m
40
40
解:(1)设每件涨价n元,利润为y1.
则y1=(60+n
–
40
)(300
–
10n)
即y1=-10n2+100n+6000
其中,0≤n≤30.
利润
=
售价×销量-进价×销量
=
(售价-进价)×销量
怎样确定n的取值范围?
可得:0≤n≤30.
y1=-10n2+100n+6000
(0≤n≤30)
抛物线y1
=-10n2+100n+6000顶点坐标为
,所以商品的单价上涨
元时,利润最大,为
元.
(5,6250)
5
6250
n取何值时,y有最大值?最大值是多少?
=-10(n2-10n)+6000
=-10(n-5)2+6250
即涨价情况下,定价65元时,有最大利润6250元.
涨价:
进价/元
售价/元
销量/件
利润
降价
40
60-m
300+20m
解:
(2)设每件降价m元,利润为y2.
则y2=(60-m
–
40
)(300
+20m)
即y2=-20m2+100m+6000
其中,0≤m≤20.
怎样确定m的取值范围?
可得:0≤m≤20.
降价情况下的最大利润又是多少呢?
y2=-20m2+100m+6000
(0≤m≤20)
抛物线y2=-20m2+100m+6000顶点坐标为
,所以商品的单价下降
元时,利润最大,为
元.
(2.5,6125)
2.5
6125
m取何值时,y有最大值?最大值是多少?
即降价情况下,定价57.5元时,有最大利润6125元.
降价:
=-20(m2-5m)+6000
=-20(m-2.5)2+6125
(2)降价情况下,定价57.5元时,有最大利润6125元.
(1)涨价情况下,定价65元时,有最大利润6250元.
综上可知:
该商品的价格定价为65元时,可获得最大利润6250元.
随堂练习
1.如图,四边形的两条对角线AC、BD互相垂直,AC+
BD=10,当AC、BD的长是多少时,四边形ABCD的面
积最大?
解:设AC=x,四边形ABCD面积为y,
则BD=(10-x).
即当AC、BD的长均为5时,四边形ABCD的面积最大.
2.用一段长为30m的篱笆围成一个一边靠墙的矩形菜园(如图所示),墙长为18m,这个矩形的长,宽各为多少时,菜园的面积最大,最大面积是多少?
解:设矩形的长为x
m,面积为y
m2,则矩形的宽为
m.
∴0
解:设矩形的长为xcm,圆柱的侧面积为ycm2,
则矩形的宽为(18-x)cm,绕矩形的长或宽旋转,圆柱的侧面积相等.
有y=2πx(18-x)=-2π(x-9)2+162π(0<x<18).
当x=9时,y有最大值为162π.
即当矩形的长、宽各为9cm时,圆柱的侧面积最大。
4.某种商品每件的进价为30元,在某段时间内若以每件x元出售,可卖出(200-x)件,应如何定价才能使利润最大?
解:设所得利润为y元,
由题意得y=x(200-x)-30(200-x)
=-x2+230x-6000
=-(x-115)2+7225
(0
即当这件商品定价为115元时,利润最大.
5.某种文化衫以每件盈利20元的价格出售,每天可售出40件.
若每件降价1元,则每天可多售10件,如果每天要盈利最多,每件应降价多少元?
解:设每件应降价x元,每天的利润为y元,
由题意得:y=(20-x)(40+10x)
=-10x2+160x+800
=-10(x-8)2+1440
(0<x<20).
当x=8时,y取最大值1440.
即当每件降价8元时,每天的盈利最多。
课堂小结
图形面积最值问题:
由图形面积公式直接计算列出关系式,再利用二次函数的性质分析、解决问题.
利用二次函数解决利润问题的一般步骤:
①审清题意,理解问题;②分析问题中的变量和常量以及数量之间的关系;③列出函数关系式;④求解数学问题;⑤求解实际问题.
课后作业
1.完成课本课后习题;
2.完成练习册本课时的习题。
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
