第21章 21.4 第3课时 利用二次函数模型解决抛物线形运动轨迹问题 课件(共17张PPT)
文档属性
| 名称 | 第21章 21.4 第3课时 利用二次函数模型解决抛物线形运动轨迹问题 课件(共17张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-16 21:38:54 | ||
图片预览





文档简介
(共17张PPT)
第3课时
利用二次函数模型解决抛物线形运动轨迹问题
21.4
二次函数的应用
沪科版
九年级数学上册
上课课件
学习目标
【知识与技能】
能为一些较简单的生活实际问题建立二次函数模型,并在此基础上,根据二次函数关系式和图象特点,从而解决实际问题.
【过程与方法】
经历探索问题的过程,获得利用数学方法解决实际问题的经验,感受数学模型和数学应用的价值,通过观察、比较、推理、交流等过程,发展获得一些研究问题与合作交流的方法与经验.
【情感态度】
通过动手实做及同学之间的合作与交流,让学生积累经验,发展学习动力.
【教学重点】
会根据不同的条件,利用二次函数解决生活中的实际问题.
【教学难点】
利用二次函数解决生活中的实际问题.
新课导入
问题:从地面竖直向上抛出一小球,小球的高度h(单位:m)与小球的运动时间t(单位:s)之间的关系式是h=30t-5t2
(0≤t≤6).
小球运动的时间是多少时,小球最高?小球运动中的最大高度是多少?
推进新课
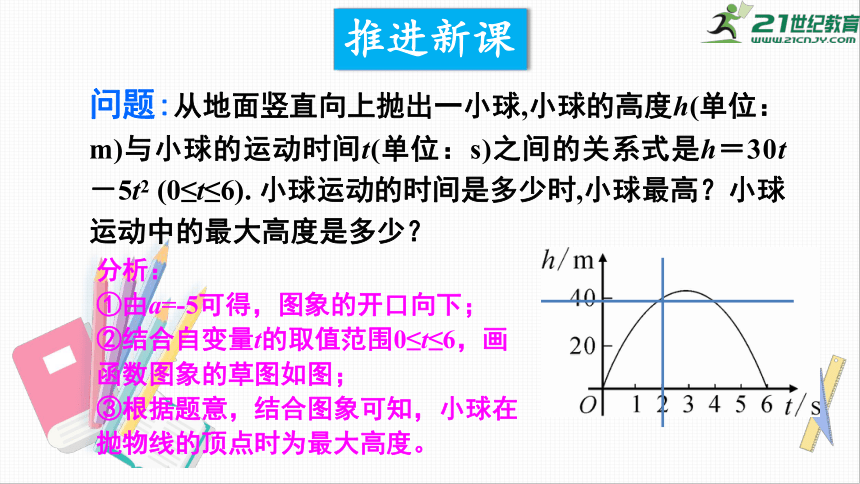
问题:从地面竖直向上抛出一小球,小球的高度h(单位:m)与小球的运动时间t(单位:s)之间的关系式是h=30t-5t2
(0≤t≤6).
小球运动的时间是多少时,小球最高?小球运动中的最大高度是多少?
分析:
①由a=-5可得,图象的开口向下;
②结合自变量t的取值范围0≤t≤6,画函数图象的草图如图;
③根据题意,结合图象可知,小球在抛物线的顶点时为最大高度。
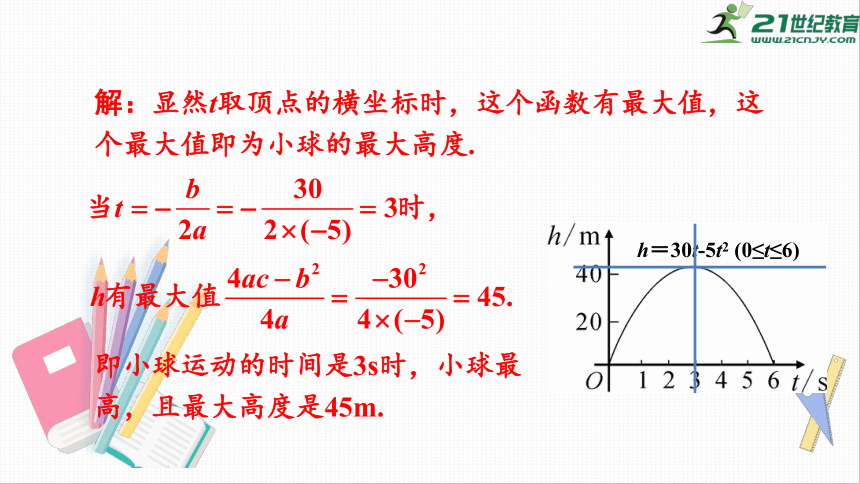
解:显然t取顶点的横坐标时,这个函数有最大值,这个最大值即为小球的最大高度.
h=30t-5t2
(0≤t≤6)
即小球运动的时间是3s时,小球最高,且最大高度是45m.
一般地,当a>0(a<0)时,抛物线
y
=
ax2
+
bx
+
c的顶点有最低(高)点,也就是说,当x=
时,二次函数有最小(大)值
。
上抛物体在不计空气阻力的情况下,有如下的表达式
其中h是物体上升的高度,V0是物体被上抛时竖直向上的初始速度,g是重力加速度(取g=10m/s2),t是物体抛出后经过的时间.
例
在一次排球比赛中,排球从靠近地面处被垫起时竖直向上的初始速度为10m/s.
(1)问排球上升的最大高度是多少?
(2)已知某运动员在2.5m高度时扣球
效果最佳,如果她要打快攻,问该运
动员在排球被垫起后多长时间扣球最佳?(精确到0.1s)
解(1)根据题意,得
因为抛物线开口向下,顶点坐标为(1,5).
答:排球上升的最大高度是5m.
(2)当h=2.5m时,得
10t-5t2=2.5.
解方程,得
t1≈0.3(s),
t2≈1.7(s).
在排球上升和下落中,各有一次经过2.5m高度,但第一次经过时离排球被垫起仅有0.3s,要打快攻,选择此时扣球,可令对方措手不及,易获成功.
答:该运动员应在排球被垫起后0.3s时扣球最佳.
随堂练习
1.把一个小球以20m/s的速度竖直向上弹出,它在空中高度h(m)与时间t(s)满足关系:h=20t-5t2,当h=20时,小球的运动时间为(
)
A.20s
B.2s
B
2.在距离地面2m高的某处把一物体以初速度v0(m/s)竖直向上抛出,咋不计空气阻力的情况下,其上升高度s(m)与抛出时间t(s)满足:
(其中g是常数,通常取10m/s2).若v0=10m/s,则该物体在运动过程中最高点距地面(
)
A.5m
B.6m
C.7m
D.8m
C
3.
校运动会上,小明参加铅球比赛,若某次试掷,铅球飞行的高度y(m)与水平距离x(m)之间的函数关系式为
,求小明这次试掷的成绩及铅球出手时的高度.
试掷的成绩:10m
铅球出手时的高度:
m
课堂小结
一般地,当a>0(a<0)时,抛物线
y
=
ax2
+
bx
+
c的顶点有最低(高)点,也就是说,当x=
时,二次函数有最小(大)值
。
课后作业
1.完成课本课后习题;
2.完成练习册本课时的习题。
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
第3课时
利用二次函数模型解决抛物线形运动轨迹问题
21.4
二次函数的应用
沪科版
九年级数学上册
上课课件
学习目标
【知识与技能】
能为一些较简单的生活实际问题建立二次函数模型,并在此基础上,根据二次函数关系式和图象特点,从而解决实际问题.
【过程与方法】
经历探索问题的过程,获得利用数学方法解决实际问题的经验,感受数学模型和数学应用的价值,通过观察、比较、推理、交流等过程,发展获得一些研究问题与合作交流的方法与经验.
【情感态度】
通过动手实做及同学之间的合作与交流,让学生积累经验,发展学习动力.
【教学重点】
会根据不同的条件,利用二次函数解决生活中的实际问题.
【教学难点】
利用二次函数解决生活中的实际问题.
新课导入
问题:从地面竖直向上抛出一小球,小球的高度h(单位:m)与小球的运动时间t(单位:s)之间的关系式是h=30t-5t2
(0≤t≤6).
小球运动的时间是多少时,小球最高?小球运动中的最大高度是多少?
推进新课
问题:从地面竖直向上抛出一小球,小球的高度h(单位:m)与小球的运动时间t(单位:s)之间的关系式是h=30t-5t2
(0≤t≤6).
小球运动的时间是多少时,小球最高?小球运动中的最大高度是多少?
分析:
①由a=-5可得,图象的开口向下;
②结合自变量t的取值范围0≤t≤6,画函数图象的草图如图;
③根据题意,结合图象可知,小球在抛物线的顶点时为最大高度。
解:显然t取顶点的横坐标时,这个函数有最大值,这个最大值即为小球的最大高度.
h=30t-5t2
(0≤t≤6)
即小球运动的时间是3s时,小球最高,且最大高度是45m.
一般地,当a>0(a<0)时,抛物线
y
=
ax2
+
bx
+
c的顶点有最低(高)点,也就是说,当x=
时,二次函数有最小(大)值
。
上抛物体在不计空气阻力的情况下,有如下的表达式
其中h是物体上升的高度,V0是物体被上抛时竖直向上的初始速度,g是重力加速度(取g=10m/s2),t是物体抛出后经过的时间.
例
在一次排球比赛中,排球从靠近地面处被垫起时竖直向上的初始速度为10m/s.
(1)问排球上升的最大高度是多少?
(2)已知某运动员在2.5m高度时扣球
效果最佳,如果她要打快攻,问该运
动员在排球被垫起后多长时间扣球最佳?(精确到0.1s)
解(1)根据题意,得
因为抛物线开口向下,顶点坐标为(1,5).
答:排球上升的最大高度是5m.
(2)当h=2.5m时,得
10t-5t2=2.5.
解方程,得
t1≈0.3(s),
t2≈1.7(s).
在排球上升和下落中,各有一次经过2.5m高度,但第一次经过时离排球被垫起仅有0.3s,要打快攻,选择此时扣球,可令对方措手不及,易获成功.
答:该运动员应在排球被垫起后0.3s时扣球最佳.
随堂练习
1.把一个小球以20m/s的速度竖直向上弹出,它在空中高度h(m)与时间t(s)满足关系:h=20t-5t2,当h=20时,小球的运动时间为(
)
A.20s
B.2s
B
2.在距离地面2m高的某处把一物体以初速度v0(m/s)竖直向上抛出,咋不计空气阻力的情况下,其上升高度s(m)与抛出时间t(s)满足:
(其中g是常数,通常取10m/s2).若v0=10m/s,则该物体在运动过程中最高点距地面(
)
A.5m
B.6m
C.7m
D.8m
C
3.
校运动会上,小明参加铅球比赛,若某次试掷,铅球飞行的高度y(m)与水平距离x(m)之间的函数关系式为
,求小明这次试掷的成绩及铅球出手时的高度.
试掷的成绩:10m
铅球出手时的高度:
m
课堂小结
一般地,当a>0(a<0)时,抛物线
y
=
ax2
+
bx
+
c的顶点有最低(高)点,也就是说,当x=
时,二次函数有最小(大)值
。
课后作业
1.完成课本课后习题;
2.完成练习册本课时的习题。
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
